Арифметическая прогрессия
Знаменитый ученый Карл Гаусс однажды сказал:
«Ничего не сделано, если что-то осталось недоделанным.»
Поэтому давай сейчас разберем одну из важнейших тем алгебры – арифметическую прогрессию.
А если остались какие-то пробелы, заполним их.
Кстати, Гаусса мы вспомнили не просто так 🙂
Вперёд!
Арифметическая прогрессия — коротко о главном
Определение арифметической прогрессии:
Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна \( \displaystyle d\).
Например:
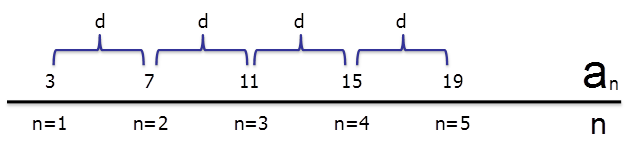
- \( {{a}_{1}}=3\)
- \( \displaystyle {{a}_{2}}=3+d=7~\Rightarrow d=7-3=4\)
- \( \displaystyle {{a}_{3}}=7+4=11\) и т.д.
Арифметическая прогрессия бывает возрастающей (\( \displaystyle d>0\)) и убывающей (\( \displaystyle d<0\)).
Формула нахождения n-ого члена арифметической прогрессии:
\( {{a}_{n}}={{a}_{1}}+d\left( n-1 \right)\) , где \( \displaystyle n\)– количество чисел в прогрессии.
Как найти член прогрессии, если известны его соседние члены:
\( {{\text{a}}_{\text{n}}}=\frac{{{\text{a}}_{\text{n}+1}}+{{\text{a}}_{\text{n}-1}}}{2}\) — где \( \displaystyle n\) – количество чисел в прогрессии.
Сумма членов арифметической прогрессии:
1-й способ: \( {{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\), где \( \displaystyle n\) – количество значений.
2-й способ: \( \displaystyle {{s}_{n}}=\frac{2{{a}_{1}}+d\left( n-1 \right)}{2}\cdot n\), где \( \displaystyle n\) – количество значений.
Числовая последовательность
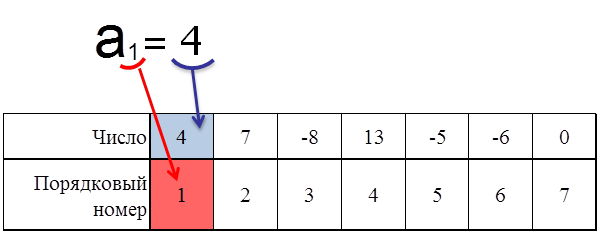
Итак, сядем и начнем писать какие-нибудь числа. Например: \( \displaystyle 4,\text{ }7,\text{ }-8,\text{ }13,\text{ }-5,\text{ }-6,\text{ }0,\text{ }\ldots \)
Писать можно любые числа, и их может быть сколько угодно (в нашем случае их \( \displaystyle 7\)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.
Это и есть пример числовой последовательности.
Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.
Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и \( \displaystyle n\)-ное число) всегда одно.
Число с номером \( \displaystyle n\) называется \( \displaystyle n\)-ным членом последовательности.
Всю последовательность мы обычно называем какой-нибудь буквой (например, \( \displaystyle a\)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: \( \displaystyle {{a}_{1}},\text{ }{{a}_{2}},\text{ }…,\text{ }{{a}_{10}},\text{ }…,\text{ }{{a}_{n}}\).
Арифметическая прогрессия — определения
Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.
Например:
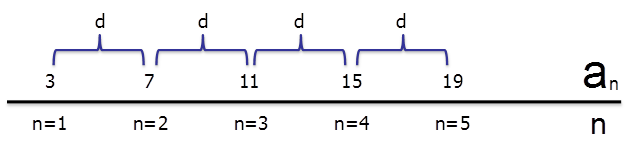
Такая числовая последовательность называется арифметической прогрессией.
Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.
Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.
Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.
Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:
- \( \displaystyle 3;\text{ }6;\text{ }9;\text{ }12;\text{ }15;\text{ }17\ldots \)
- \( \displaystyle 1;\text{ }12;\text{ }23;\text{ }34;\text{ }45\text{ }\ldots \)
- \( \displaystyle -5;\text{ }-1;\text{ }3;\text{ }7;\text{ }11;\text{ }15\ldots \)
- \( \displaystyle -6;\text{ }5;\text{ }17;\text{ }28;\text{ }39\ldots \)
Разобрался? Сравним наши ответы:
Является арифметической прогрессией – 2, 3.
Не является арифметической прогрессией – 1, 4.
Вернемся к заданной прогрессии (\( \displaystyle 3;\text{ }7;\text{ }11;\text{ }15;\text{ }19\ldots \)) и попробуем найти значение ее 6-го члена.
Существует два способа его нахождения.
Нахождения n-ого члена арифметической прогрессии
Способ I
Мы можем прибавлять к предыдущему значению числа прогрессии \( d=4\) , пока не дойдем до \( \displaystyle 6\)-го члена прогрессии. Хорошо, что суммировать нам осталось немного – всего три значения:
\( \begin{array}{l}{{a}_{4}}=11+4=15\\{{a}_{5}}=15+4=19\\{{a}_{6}}=19+4=23\end{array}\)
Итак, 6-ой член описанной арифметической прогрессии равен 23.
Способ II
А что если нам нужно было бы найти значение \( \displaystyle 140\)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.
А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.
Это и есть математика!
Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка.
Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.
Что мы знаем?
- У нас есть арифметическая прогрессия: 3, 7, 11, 15, 19 и т.д.
- У нас есть номера прогрессии: 1, 2, 3, 4, 5, и т.д.
- Мы все время прибавляем 4, значит разница прогрессии d = 4.
Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.
7=3+4 или 7=3+d
Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?
11=3+4+4 или 11=3+d+d
Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.
Давай проверим? Чему равен 4-й член арифметической прогрессии?
15=3+4+4+4 или 15=3+d+d+d
Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!
Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа.
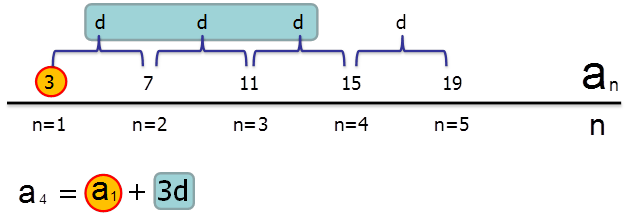
А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.
Например, посмотрим, из чего складывается значение \( \displaystyle 4\)-го члена данной арифметической прогрессии:
\( \begin{array}{l}{{a}_{4}}={{a}_{1}}+d\left( 4-1 \right)\\{{a}_{4}}=3+4\left( 4-1 \right)=15\end{array}\)Попробуй самостоятельно найти таким способом значение члена \( \displaystyle n=6\) данной арифметической прогрессии.
Рассчитал? Сравни свои записи с ответом:
\( \begin{array}{l}{{a}_{6}}={{a}_{1}}+d\left( 6-1 \right)\\{{a}_{6}}=3+4\left( 6-1 \right)=3+4\cdot 5=3+20=23\end{array}\)Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли \( \displaystyle d\) к предыдущему значению членов арифметической прогрессии.
Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:
\( {{a}_{n}}={{a}_{1}}+d\left( n-1 \right)\) – уравнение арифметической прогрессии.
Кстати, таким образом мы можем посчитать и \( \displaystyle 140\)-ой член данной арифметической прогрессии (да и \( \displaystyle 169\)-ый тоже можем, да и любой другой вычислить совсем несложно).
Попробуй посчитать значения \( \displaystyle 140\)-го и \( \displaystyle 169\)-го членов, применив полученную формулу.
\( \begin{array}{l}…\\{{a}_{140}}={{a}_{1}}+d\left( 140-1 \right)\\{{a}_{140}}=3+4\left( 140-1 \right)=3+4\cdot 139=3+556=559\\{{a}_{169}}={{a}_{1}}+d\left( 169-1 \right)\\{{a}_{169}}=3+4\left( 169-1 \right)=3+4\cdot 168=3+672=675\end{array}\)Возрастающие и убывающие арифметические прогрессии
Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.
Например:
\( \displaystyle \begin{array}{l}4;\text{ }6;\text{ }8;\text{ }10;\text{ }12\\-2;\text{ }4;\text{ }10;\text{ }16;\text{ }20\end{array}\)Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.
Например:
\( \displaystyle \begin{array}{l}12;\text{ }10;\text{ }8;\text{ }6;\text{ }4\\4;\text{ }0;\text{ }-4;\text{ }-8;\text{ }-12.\end{array}\)Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.
Проверим это на практике.
Нам дана арифметическая прогрессия, состоящая из следующих чисел: \( \displaystyle 13;\text{ }8;\text{ }4;\text{ }0;\text{ }-4.\)
Проверим, какое получится \( \displaystyle 4\)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:
\( {{\text{a}}_{\text{n}}}={{\text{a}}_{1}}+\text{d}\left( \text{n}-1 \right)\)\( \displaystyle d=8-13=-5\)Заметим, что так как арифметическая прогрессия убывающая, то значение \( \displaystyle d\) будет отрицательным, ведь каждый последующий член меньше предыдущего.
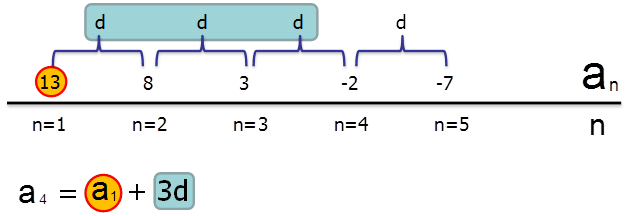
Так как \( \displaystyle d=-5\), то:
\( {{a}_{4}}=13-5\left( 4-1 \right)=13-15=-2\)
Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.
Попробуй самостоятельно найти \( \displaystyle 140\)-ой и \( \displaystyle 169\)-ый члены этой арифметической прогрессии.
Сравним полученные результаты:
\( \begin{array}{l}{{a}_{140}}={{a}_{1}}+d\left( 140-1 \right)\\{{a}_{140}}=13-5\left( 140-1 \right)=13-5\cdot 139=13-695=-682\\{{a}_{169}}={{a}_{1}}+d\left( 169-1 \right)\\{{a}_{169}}=13-5\left( 169-1 \right)=13-5\cdot 168=13-840=-827\end{array}\)Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)
Усложним задачу — выведем свойство арифметической прогрессии.
Допустим, нам дано такое условие:
\( \displaystyle 4;\text{ }x;\text{ }12\ldots \) — арифметическая прогрессия, найти значение \( \displaystyle x\).
Легко, скажешь ты и начнешь считать по уже известной тебе формуле:
\( {{a}_{n}}={{a}_{1}}+d\left( n-1 \right)\)Пусть \( \displaystyle {{a}_{1}}=4\), а \( \displaystyle {{a}_{3}}=12\), тогда:
\( \displaystyle \begin{array}{l}{{a}_{3}}={{a}_{1}}+d\left( 3-1 \right)\\12=4+2d~~\Rightarrow ~d=\frac{12-4}{2}=4\\{{a}_{2}}=x={{a}_{1}}+d\\{{a}_{2}}=x=4+4=8\end{array}\)Абсолютно верно.
Получается, мы сначала находим \( \displaystyle d\), потом прибавляем его к первому числу и получаем искомое \( \displaystyle x\).
Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа \( \displaystyle 4024;~x;6072\)?
Согласись, есть вероятность ошибиться в вычислениях.
А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?
Конечно да, и именно ее мы попробуем сейчас вывести.
Обозначим искомый член арифметической прогрессии как \( {{\text{a}}_{\text{n}}}\), формула его нахождения нам известна – это та самая формула, выведенная нами в начале:
\( {{a}_{n}}={{a}_{1}}+d\left( n-1 \right)\), тогда:
- предыдущий член прогрессии это \( {{a}_{n}}-d\): \( {{a}_{n-1}}={{a}_{1}}+d\left( n-1 \right)-d\)
- последующий член прогрессии это \( {{a}_{n}}+d\): \( {{a}_{n+1}}={{a}_{1}}+d\left( n-1 \right)+d\)
Просуммируем предыдущий и последующий члены прогрессии:
\( {{a}_{1}}+d\left( n-1 \right)-d+{{{a}}_{1}}+\text{d}\left( \text{n}-1 \right)+\text{d}=2\left( {{a}_{1}}+d\left( n-1 \right) \right)\text{ }\!\!~\!\!\text{ }\)Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.
Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на \( 2\).
\( {{a}_{n}}=\frac{{{a}_{n+1}}+{{a}_{n-1}}}{2}\) – свойство членов арифметической прогрессии.
Попробуем посчитать значение \( x\), используя выведенную формулу:
\( x=\frac{4+12}{2}=8\)Все верно, мы получили это же число. Закрепим материал.
Посчитай значение \( x\) для прогрессии \( \displaystyle 4024;~x;6072\) самостоятельно, ведь это совсем несложно.
\( x=\frac{4024+6072}{2}=5048\)Молодец! Ты знаешь о прогрессии почти все!
Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…
Сумма первых n членов арифметической прогрессии
Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:
«Сосчитать сумму всех натуральных чисел от \( \displaystyle 1\) до \( \displaystyle 40\) (по другим источникам до \( \displaystyle 100\)) включительно».
Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…
Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.
Допустим, у нас есть арифметическая прогрессия, состоящая из \( \displaystyle 6\)-ти членов: \( \displaystyle 6;\text{ }8;\text{ }10;\text{ }12;\text{ }14;\text{ }16…\)
Нам необходимо найти сумму данных \( \displaystyle 6\) членов арифметической прогрессии.
Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму \( \displaystyle 100\) ее членов, как это искал Гаусс?
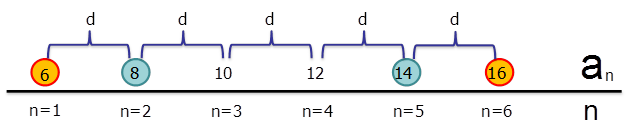
Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.
Попробовал? Что ты заметил? Правильно! Их суммы равны
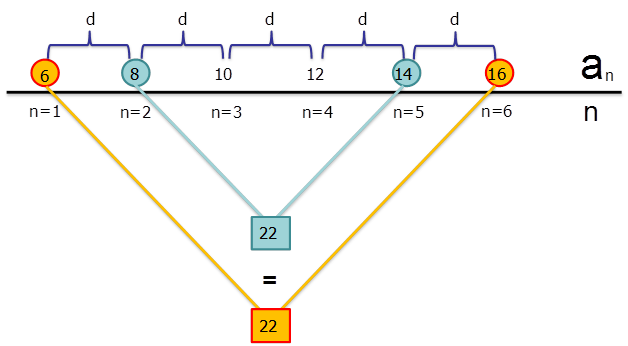
А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?
Конечно, ровно половина всех чисел, то есть \( \frac{6}{2}=3\).
Исходя из того, что сумма двух членов арифметической прогрессии равна \( 22\), а подобных равных пар \( 3\), мы получаем, что общая сумма равна:
\( \displaystyle S\text{ }=\text{ }22\cdot 3\text{ }=\text{ }66\).
Таким образом, формула для суммы первых \( \displaystyle n\) членов любой арифметической прогрессии будет такой:
\( \displaystyle {{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\), где \( \displaystyle n\) – количество значений.
В некоторых задачах нам неизвестен \( \displaystyle n\)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу \( \displaystyle n\)-го члена. \( {{a}_{n}}={{a}_{1}}+d\left( n-1 \right)\)
Что у тебя получилось?
\( \displaystyle {{S}_{n}}=\frac{2{{a}_{1}}+d\left( n-1 \right)}{2}\cdot n\), где \( \displaystyle n\) – количество значений.
Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма \( \displaystyle 40\) чисел, начиная от \( \displaystyle 1\)-го, и сумма \( \displaystyle 100\) чисел начиная от \( \displaystyle 1\)-го.
Сколько у тебя получилось?
У Гаусса получилось, что сумма \( \displaystyle 100 \) членов равна \( \displaystyle 5050\), а сумма \( \displaystyle 40 \) членов \( \displaystyle 820\).
Так ли ты решал?
- \( {{S}_{40}}=\frac{\left( 1+40 \right)\cdot 40}{2}=\frac{41\cdot 40}{2}=\frac{1640}{2}=820\)
- \( {{S}_{100}}=\frac{\left( 1+100 \right)\cdot 100}{2}=\frac{101\cdot 100}{2}=5050\)
На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.
Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется \( \displaystyle 6\) блочных кирпичей.
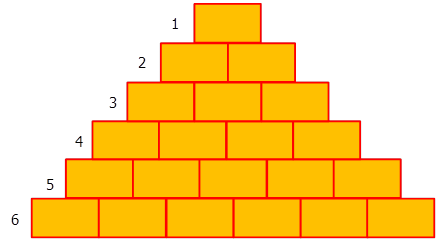
Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?
В данном случае прогрессия выглядит следующим образом:
\( \displaystyle 6;\text{ }5;\text{ }4;\text{ }3;\text{ }2;\ 1\).
Разность арифметической прогрессии \( \displaystyle ~=\text{ }d\text{ }=\text{ }-1\).
Количество членов арифметической прогрессии \( \displaystyle=6\).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Разность арифметической прогрессии \( \displaystyle ~=\text{ }d\text{ }=\text{ }-1\).
Количество членов арифметической прогрессии \( \displaystyle=6\).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Способ 1.
\( \begin{array}{l}{{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\\~~{{S}_{6}}=\frac{\left( 6+1 \right)\cdot 6}{2}=\frac{7\cdot 6}{2}=21\\~\end{array}\)
Способ 2.
\( \displaystyle {{S}_{n}}=\frac{2{{a}_{1}}+d\left( n-1 \right)}{2}\cdot n\)
\( {{S}_{n}}=\frac{2\cdot 6+1\left( 6-1 \right)}{2}\cdot 6=\frac{12+5\cdot 6}{2}=\frac{7\cdot 6}{2}=\frac{42}{2}=21\)
А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.
Сошлось?
Молодец, ты освоил сумму \( \displaystyle n\)-ных членов арифметической прогрессии.
Конечно, из \( \displaystyle 6\) блоков в основании пирамиду не построишь, а вот из \( \displaystyle 60\)?
Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – \( \displaystyle 1830\) блоков:
\( \begin{array}{l}{{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\\{{S}_{60}}=\frac{\left( 60+1 \right)\cdot 60}{2}=\frac{61\cdot 60}{2}=61\cdot 30=1830.\end{array}\)Задачи для самостоятельной работы
- Маша приходит в форму к лету. Ежедневно она увеличивает количество приседаний на 5. Сколько раз будет приседать Маша через 2 недели, если на первой тренировке она сделала 10 приседаний.
- Какова сумма всех нечетных чисел, содержащихся в 20.
- Лесорубы при хранении бревен укладывают их таким образом, что каждый верхний слой содержит на одно бревно меньше, чем предыдущий. Сколько бревен находится в одной кладке, если основанием кладки служат 14 бревен.
- В арифметической прогрессии \( \displaystyle -5,\ \ -2,\ \ 1,\ \ 4\ \ …\) найти формулу n-го члена и найти сотый член.
- Найдите сумму всех двузначных чисел, кратных \( \displaystyle 4\).
- Ежедневно спортсмен пробегает на \( \displaystyle 100\) м больше, чем в предыдущий день. Сколько всего километров он пробежит за \( \displaystyle 2\) недели, если в первый день он пробежал \( \displaystyle 2\) км \( \displaystyle 400\) м?
- Велосипедист проезжает каждый день на \( \displaystyle 2\) км больше, чем в предыдущий. В первый день он проехал \( \displaystyle 16\) км. Сколько дней ему надо ехать, чтобы преодолеть \( \displaystyle 250\) км? Сколько километров он проедет за последний день пути?
- Цена холодильника в магазине ежегодно уменьшается на одну и ту же сумму. Определите, на сколько каждый год уменьшалась цена холодильника, если, выставленный на продажу за \( \displaystyle 20000\) рублей, через шесть лет был продан за \( \displaystyle 12750\) рублей.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Ваш сайт просто чудо!
Спасибо, Валерій! Регистрируйтесь также на наш канал на YouTube. Там тоже много полезного материала для подготовки: https://www.youtube.com/YoucleverOrg100