Вписанный и центральный угол окружности
С появлением окружности, а затем колеса человечество сильно упростило себе жизнь.
И через много веков на ЕГЭ появились задачи по этой теме, конечно же 🙂
Зная свойства вписанного и центрального угла окружности, ты сможешь решить множество таких задач. И в этой статье мы тебе с этим поможем.
- Как измерить дуги и окружности
- Свойства вписанного угла и следствия из них
- Как выразить углы между хордами и секущими через центральный угол
- и многое другое…
Поехали!
Вписанный и центральный угол окружности — коротко о главном
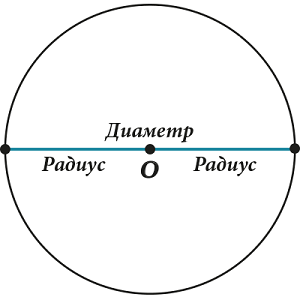
Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.
Радиус – отрезок, соединяющий центр и точку на окружности.
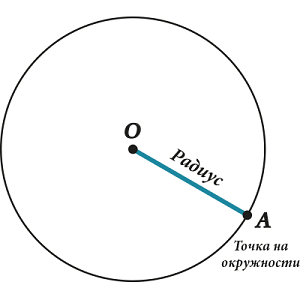
Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.
Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.
А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».
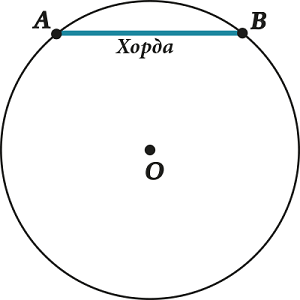
Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда \( \displaystyle AB\) стягивает дугу \( \displaystyle AB\).
А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».
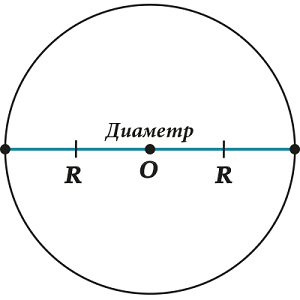
Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же,
Радиус равен половине диаметра.
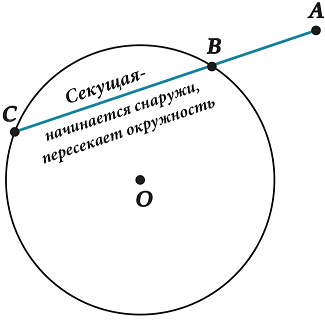
Кроме хорд бывают еще и секущие.
Вспомнили самое простое?
А теперь – названия для углов.
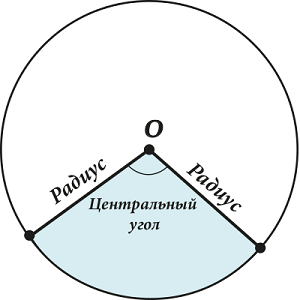
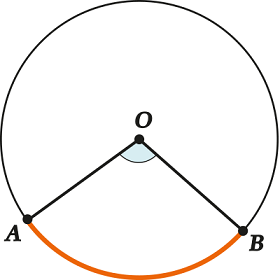
Центральный угол – угол между двумя радиусами.
Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.
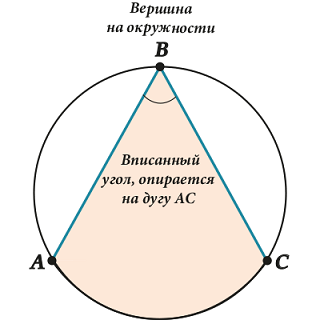
А теперь – вписанный угол.
Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
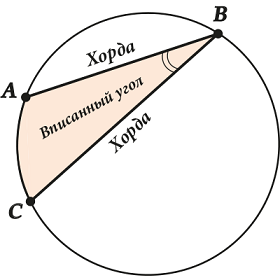
При этом говорят, что вписанный угол \( \displaystyle ABC\) опирается на дугу (или на хорду) \( \displaystyle AC\).
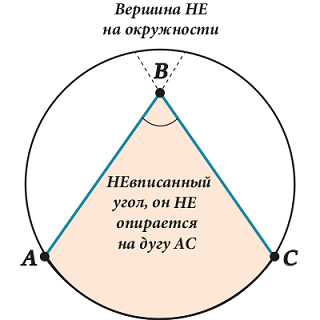
Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.
Смотри на картинку:
Измерение дуг и углов окружности
Длина окружности. Дуги и углы измеряются в градусах и радианах.
Сперва о градусах
Для углов проблем нет – нужно научиться измерять дугу в градусах.
Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла
Что здесь значит слово «соответствующего»? Смотрим внимательно:
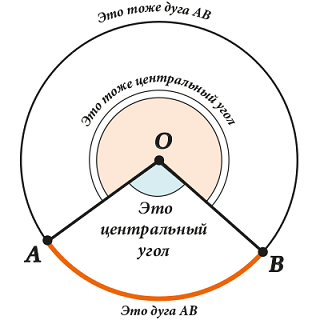
Видишь две дуги \( \displaystyle AB\) и два центральных угла?
Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше \( \displaystyle 180{}^\circ \)), а меньшей дуге соответствует меньший угол.
Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.
А теперь о радианах
Что же это за зверь такой «радиан»?
Представь себе: радианы – это способ измерения угла … в радиусах!
Угол величиной \( \displaystyle 1\) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.
Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?
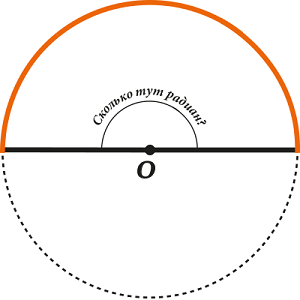
Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?
Этим вопросом задавались учёные ещё в Древней Греции.
И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде \( \displaystyle 1,\text{ }2,\text{ }3,\frac{7}{5},\frac{2}{239}\) и т.п.
И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в \( \displaystyle 2,5\) раза или в \( \displaystyle \sqrt{17}\) раз больше радиуса!
Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву \( \displaystyle \pi \).
Итак, \( \displaystyle \pi \) – это число, выражающее отношение длины полуокружности к радиусу.
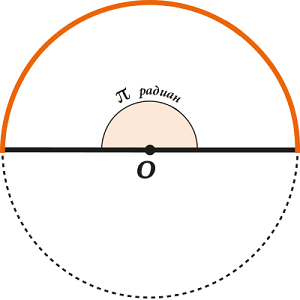
Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём \( \displaystyle \pi \) радиан. Именно оттого, что половина окружности в \( \displaystyle \pi \) раз больше радиуса.
Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число \( \displaystyle \pi \), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что
\( \displaystyle \pi \approx 3,14\)
Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна \( \displaystyle 6,28\), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква \( \displaystyle \pi \).
И тогда эта длина окружности окажется равной \( \displaystyle 2\pi \). И конечно, длина окружности радиуса \( \displaystyle R\) равна \( \displaystyle 2\pi R\).
Вернёмся к радианам.
Мы выяснили уже, что в развёрнутом угле содержится \( \displaystyle \pi \) радиан.
Исходя из этого, можно пересчитать любые углы «в градусах» на углы «в радианах». Для этого нужно просто решить пропорцию! Давай попробуем. Возьмём угол в \( \displaystyle 30{}^\circ \).
Что имеем:
\( \displaystyle 180{}^\circ -\pi \) рад.
\( \displaystyle 30{}^\circ -\ x\) рад.
Значит, \( \displaystyle x=\frac{30{}^\circ \text{ }\!\!\pi\!\!\text{ }}{180{}^\circ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\)рад., то есть \( \displaystyle 30{}^\circ =\frac{\pi }{6}\)рад. Таким же образом получается табличка с наиболее популярными углами.
| \( \displaystyle 30{}^\circ\) | \( \displaystyle \frac{\pi }{6}\) |
| \( \displaystyle 45{}^\circ\) | \( \displaystyle \frac{\pi }{4}\) |
| \( \displaystyle 90{}^\circ\) | \( \displaystyle \frac{\pi }{2}\) |
| \( \displaystyle 180{}^\circ\) | \( \displaystyle \pi \) |
| \( \displaystyle 270{}^\circ\) | \( \displaystyle \frac{3\pi }{2}\) |
| \( \displaystyle 360{}^\circ\) | \( \displaystyle 2\pi \) |
Итак, осознай и не бойся: если ты видишь букву или выражение \( \displaystyle \frac{7\pi }{2}\) и т.п., то речь идёт об угле и, по сути, запись через букву \( \displaystyle \pi\) всегда выражает, какую часть от развёрнутого угла составляет тот угол, о котором идёт речь.
А для убедительности ещё раз взгляни на табличку:
| \( \displaystyle 30{}^\circ\) | \( \displaystyle \frac{\pi }{6}\) | \( \displaystyle \frac{1}{6}\) от \( \displaystyle 180{}^\circ \), то есть от \( \displaystyle \pi \) |
| \( \displaystyle 45{}^\circ\) | \( \displaystyle \frac{\pi }{4}\) | \( \displaystyle \frac{1}{4}\) от \( \displaystyle 180{}^\circ \), то есть от \( \displaystyle \pi \) |
| \( \displaystyle 90{}^\circ\) | \( \displaystyle \frac{\pi }{2}\) | \( \displaystyle \frac{1}{2}\) от \( \displaystyle 180{}^\circ \), то есть от \( \displaystyle \pi \) |
| \( \displaystyle 180{}^\circ\) | \( \displaystyle \pi \) | это и есть \( \displaystyle \pi \) |
| \( \displaystyle 270{}^\circ\) | \( \displaystyle \frac{3\pi }{2}\) | \( \displaystyle 270{}^\circ \) в \( \displaystyle 1,5\) раза больше, чем \( \displaystyle 180{}^\circ \) |
| \( \displaystyle 360{}^\circ\) | \( \displaystyle 2\pi \) | А это \( \displaystyle 2\) раза по \( \displaystyle 180{}^\circ \), то есть \( \displaystyle 2\pi \) |
Вписанный угол вдвое меньше центрального — доказательство
Имеет место удивительный факт:
Величина вписанного угла вдвое меньше, чем величина соответствующего центрального угла.
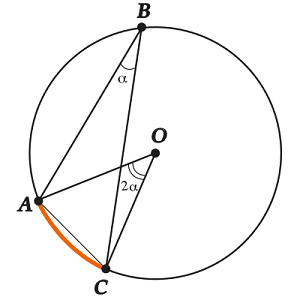
Посмотри, как это утверждение выглядит на картинке. «Соответствующий» центральный угол такой, у которого концы совпадают с концами вписанного угла, а вершина в центре.
И при этом «соответствующий» центральный угол должен «смотреть» на ту же хорду (\( \displaystyle AC\)), что и вписанный угол.
Почему же так? Почему вписанный угол вдвое меньше центрального?
Давай разберёмся сначала на простом случае.
Случай 1. Хорда проходит через центр окружности
Пусть одна из хорд проходит через центр. Ведь бывает же так иногда, верно?
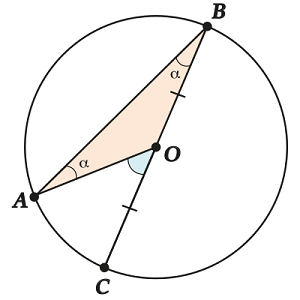
Что же тут получается? Рассмотрим \( \displaystyle \Delta AOB\). Он равнобедренный – ведь \( \displaystyle AO\) и \( \displaystyle OB\) – радиусы. Значит, \( \displaystyle \angle A=\angle B\) (обозначили их \( \displaystyle \alpha \)).
Теперь посмотрим на \( \displaystyle \angle AOC\). Это же внешний угол для \( \displaystyle \Delta AOB\)!
Значит, для этого случая доказали, что центральный угол вдвое больше вписанного.
Но уж больно частный случай: правда ведь, далеко не всегда хорда \( \displaystyle BC\) проходит прямиком через центр? Но ничего, сейчас этот частный случай нам здорово поможет.
Случай 2. Центр окружности лежит внутри угла
Смотри, второй случай: пусть центр лежит внутри \( \displaystyle \angle ABC\).
Давай сделаем вот что: проведём диаметр \( \displaystyle \text{BK}\). И тогда … видим две картинки, которые уже разбирали в первом случае.
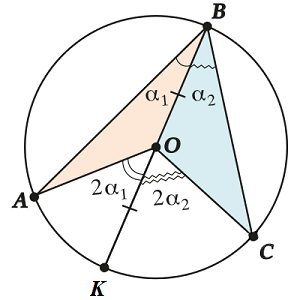
Поэтому уже имеем, что
\( \displaystyle \angle ~AOK=2~\angle ~ABK\) и \( \displaystyle \angle ~COK=2~\angle CBK\)
Но ведь:
Случай 3. Центр окружности лежит вне угла
Итак, центр лежит вне угла \( \displaystyle ABC\):
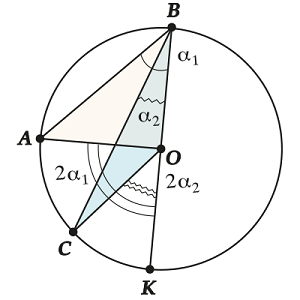
Делаем то же самое: проводим диаметр через точку \( \displaystyle \text{B}\). Все то же самое, но вместо суммы – разность.
\( \displaystyle \angle ~ABC=~{{\alpha }_{1}}-{{\alpha }_{2}}\), а \( \displaystyle \angle ~AOC=2{{\alpha }_{1}}-2{{\alpha }_{2}}\)
\( \displaystyle \angle ~AOC=2~\angle ~ABC\)
Вот и всё!
Вписанный угол вдвое меньше центрального — следствия
Давай теперь сформируем два главных и очень важных следствия из утверждения о том, что вписанный угол вдвое меньше центрального:
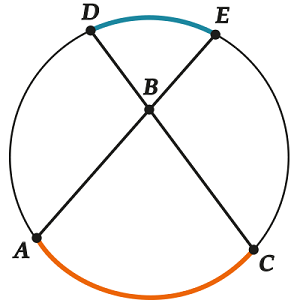
- Все вписанные углы, опирающиеся на одну дугу, равны между собой
- Следствие 2. Угол, опирающийся на диаметр – прямой
Следствие 1. Все вписанные углы, опирающиеся на одну дугу, равны между собой
Иллюстрируем:
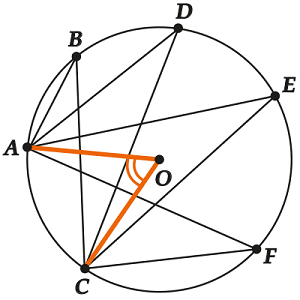
Вписанных углов, опирающихся на одну и ту же дугу (у нас эта дуга \( \displaystyle AC\)) – бесчисленное множество, они могут выглядеть совсем по-разному, но у них у всех один и тот же центральный угол (\( \displaystyle \angle ~AOC\)), а значит, все эти вписанные углы равны между собой.
Следствие 2. Угол, опирающийся на диаметр – прямой
Смотри: какой угол является центральным для \( \displaystyle \angle ABC\)?
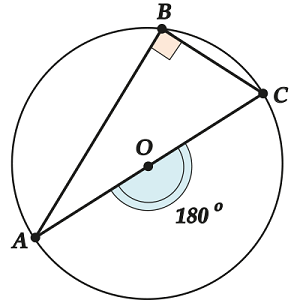
Конечно, \( \displaystyle \angle ~AOC\). Но он равен \( \displaystyle 180{}^\circ \)! Ну вот, поэтому \( \displaystyle \angle ~ABC\) (а так же ещё множество вписанных углов, опирающихся на \( \displaystyle AC\)) и равен \( \displaystyle 90{}^\circ \).
Угол между хордами и секущими, выраженный через центральный угол
А что, если интересующий нас угол НЕ вписанный и НЕ центральный, а, например, такой:
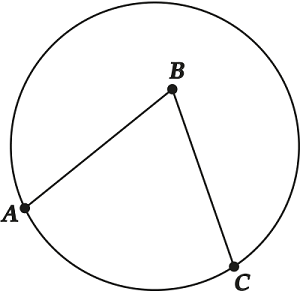
Или такой:
Можно ли его как-то выразить всё-таки через какие-то центральные углы?
Оказывается, можно.
Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол
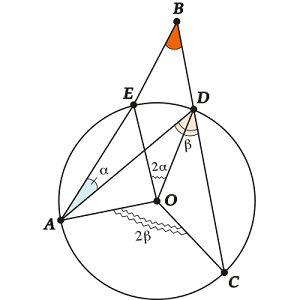
Нас интересует \( \displaystyle \angle ABC\).
\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\text{ }\!\!~\!\!\text{ }\angle \text{ }\!\!\alpha\!\!\text{ }+\angle \text{ }\!\!\beta\!\!\text{ }\) ( как внешний угол для \( \displaystyle \Delta ADB\)).
Но \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }\) — вписанный, опирается на дугу \( \displaystyle DE\) — \( \displaystyle \angle \text{ }\!\!\alpha\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{DOE}\).
\( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }\) – вписанный, опирается на дугу \( \displaystyle AC\) — \( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }=\frac{1}{2}\text{ }\!\!~\!\!\text{ }\angle \text{AOC}\).
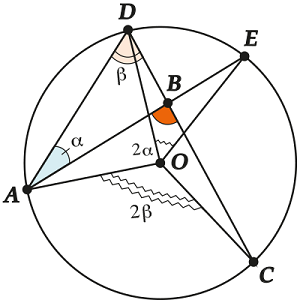
Значит, \( \displaystyle \angle ~ABC=\frac{1}{2}\angle \text{DOE}+\frac{1}{2}\angle \text{AOC}\).
Для красоты говорят:
Угол между хордами равен полусумме угловых величин дуг, заключённых в этот угол.
\( \displaystyle \angle \text{ }\!\!~\!\!\text{ ABC}=\frac{\text{AC}}{2}+\frac{\text{DE}}{2}\) – так пишут для краткости, но конечно, при использовании этой формулы нужно иметь в виду центральные углы.
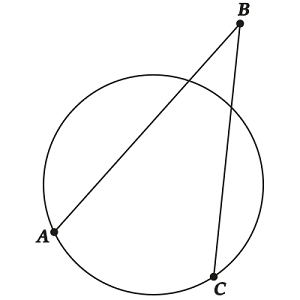
Угол между секущими равен полуразности угловых величин дуг, заключённых в этот угол
А теперь \( \displaystyle \angle ~ABC\) — «снаружи»!
Как же быть? Да почти так же!
Только теперь \( \displaystyle \angle \text{ }\!\!\beta\!\!\text{ }=\angle \text{ }\!\!\alpha\!\!\text{ }+\text{ }\!\!~\!\!\text{ }\angle \text{ABC}\) (снова применяем свойство внешнего угла для \( \displaystyle \Delta ADB\)).
То есть теперь \( \displaystyle \angle \text{ABC}=\angle \text{ }\!\!\beta\!\!\text{ }-\angle \text{ }\!\!\alpha\!\!\text{ }\).
И опять:
Ну вот, теперь ты вооружён всеми основными знаниями об углах, связанных с окружностью.
Вперёд, на штурм задач!
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте,Алексей. Спасибо вам огромное за материалы. Всё очень понятно и удобно! Дай Бог вам здоровья и благополучия!
Соня, спасибо!:)
Всё очень здорово!
Спасибо, Николай! Рады, что понравилось!
11 класс… удивилась когда наконец поняла и увидела, почему этот вписанный угол равен половине дуги, на которую он опирается
Спасибо!!!
Софья, ты крутышка! Заходи к нам еще!
Спасибо большое! Было очень понятно, без лишних слов, коротко. Никогда не думала, что смогу понять математику так быстро 🙂
Удачи Вам!
Спасибо, Зара. Математика — это просто :)) Заходите еще.
Елена
22 октября 2017
Очень полезная информация. Доступные объяснения. Здорово! Спасибо!