Угол между прямой и плоскостью
Привет!
Почти половина четверти уходит у школы на то, чтобы, изучая стереометрию, объяснить, как находятся различные углы в пространстве.
Один из таких – угол между прямой и плоскостью, очень важный момент!
А мы попробуем объяснить тебе это за 15 минут!
Поехали!
Угол между прямой и плоскостью — коротко о главном
Угол между прямой и плоскостью – это угол между прямой и её проекцией на эту плоскость.
Геометрический метод нахождения угла между прямой и плоскостью
При геометрическом методе нужно найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя представляет проекция, а потом решать планиметрическую задачу по поиску угла (\( \displaystyle \varphi \)) в треугольнике (зачастую прямоугольном).
Алгебраический метод нахождения угла между прямой и плоскостью
При алгебраическом методе вводится система координат, определяются координаты двух точек на прямой и уравнение плоскости, а затем применяется формула вычисления угла между прямой и плоскостью.
\( \displaystyle \sin \varphi =\left| \frac{A\left( {{x}_{2}}-{{x}_{1}} \right)+B\left( {{y}_{2}}-{{y}_{1}} \right)+C\left( {{z}_{2}}-{{z}_{1}} \right)}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}} \right|\)Что есть угол между прямой и плоскостью?
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.
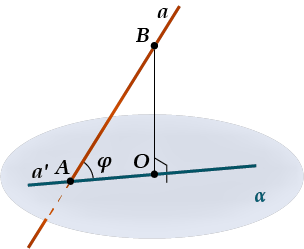
Вот, смотри: прямая \( a\) плоскость \( \displaystyle \alpha \).
Как определить угол между ними?
В соответствии с определением, которое мы только что дали), нужно опустить перпендикуляр (\( \displaystyle {{B}_{0}}\)) из любой точки прямой \( a\) на плоскость \( \displaystyle \alpha \).

А потом провести прямую через точки \( \displaystyle A\) и \( \displaystyle O\).
Эта прямая (\( \displaystyle {{a}’}\)) называется проекцией прямой \( a\) на плоскость \( \displaystyle \alpha \).
Так вот, по определению, угол между прямой \( \displaystyle a\) и плоскостью \( \displaystyle \alpha \) равен углу (\( \displaystyle \varphi \)) между \( \displaystyle a\) и \( \displaystyle {{a}’}\).
Угол между прямой и плоскостью в задачах
Как найти угол между прямой и плоскостью в задачах?
Как и в других задачах на нахождение углов и расстояний в стереометрии, есть два метода: геометрический и алгебраический.
Геометрический метод
При геометрическом методе нужно найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя представляет проекция, а потом решать планиметрическую задачу по поиску угла (\( \displaystyle \varphi \)) в треугольнике (зачастую прямоугольном).
Самый сложный момент – определить, куда опустится перпендикуляр и какая же прямая является проекцией.
Алгебраический метод
При алгебраическом методе вводится система координат, определяются координаты двух точек на прямой и уравнение плоскости, а затем применяется формула вычисления угла между прямой и плоскостью.
\( \displaystyle \sin \varphi =\left| \frac{A\left( {{x}_{2}}-{{x}_{1}} \right)+B\left( {{y}_{2}}-{{y}_{1}} \right)+C\left( {{z}_{2}}-{{z}_{1}} \right)}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}} \right|\)Здесь (\( \displaystyle {{x}_{1}},{{y}_{1}},{{z}_{1}}\)), (\( \displaystyle {{x}_{2}},{{y}_{2}},{{z}_{2}}\)) – координаты двух точек на прямой, \( \displaystyle A\), \( \displaystyle B\), \( \displaystyle C\) – координаты в уравнении плоскости: \( \displaystyle Ax+By+Cz+D=0\).
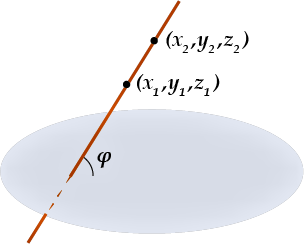
Самый сложный момент – твёрдо запомнить формулу и хорошо понимать, откуда взять все буквы для неё.
Теперь мы разберём одну задачу, где нужно найти угол между прямой и плоскостью, двумя разными способами: геометрическим и алгебраическим.
Задача по поиску угла между прямой и плоскостью
В правильной шестиугольной пирамиде \( \displaystyle SABCDEF\) точка \( \displaystyle M\) – середина ребра.
Найти угол между прямой \( \displaystyle FM\) и плоскостью основания, если \( \displaystyle SE=3FE\).
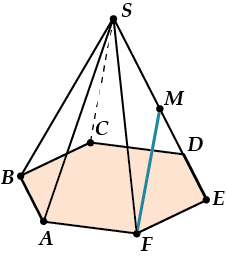
Решение задачи геометрическим методом
Поскольку в правильной пирамиде высота опускается в центр основания \( \displaystyle O\), то \( \displaystyle OE\) – это проекция \( \displaystyle SE\), а точка \( \displaystyle M\) проецируется в точку \( \displaystyle K\) – середину отрезка \( \displaystyle OE\).
И теперь \( \displaystyle FK\) – это проекция \( \displaystyle FM\), а искомый угол между прямой \( \displaystyle FM\) и плоскостью основания – это \( \displaystyle \angle MFK\).
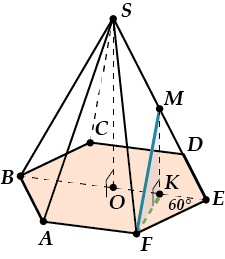
Ищем этот угол. Пусть стороны основания равны какому – то \( \displaystyle a\), тогда боковые рёбра – \( \displaystyle 3a\). Заметь, что \( \displaystyle \Delta MFK\) – прямоугольный и в этом треугольнике нам нужно найти острый угол.
Проще всего найти тангенс этого угла.
Решение задачи алгебраическим методом (методом координат)
Введём систему координат с центром в точке \( \displaystyle O\), осями \( \displaystyle Ox\) – вдоль \( \displaystyle OE\), \( \displaystyle Oy\ -\ \bot AF\) и \( \displaystyle CD\), \( \displaystyle Oz\) – вдоль \( \displaystyle OS\).
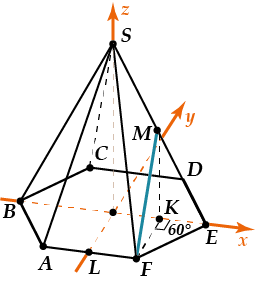
Тогда координаты точки \( \displaystyle F(\frac{a}{2};~-\frac{a\sqrt{3}}{2};0)\)
Откуда?
\( \displaystyle \text{x}=LF=\frac{a}{2}\); \( \displaystyle y=-FK=-a\sin 60{}^\circ =-\frac{a\sqrt{3}}{2}\)
Координаты точки \( \displaystyle M\):
\( \displaystyle M(OK;0;MK)\) \( \displaystyle OK=LF=\frac{a}{2};\) \( \displaystyle MK=\frac{SO}{2}=\frac{\sqrt{S{{E}^{2}}-O{{E}^{2}}}}{2}=\frac{\sqrt{9{{a}^{2}}-{{a}^{2}}}}{2}=a\sqrt{2}\)Значит \( \displaystyle M\left( \frac{a}{2};0;a\sqrt{2} \right)\)
Уравнение плоскости \( \displaystyle ABCDEF:Z=0\)
Значит, применяется формула вычисления угла между прямой и плоскостью:
Все зависит от задачи. Поэтому важно научиться пользоваться двумя методами.
Бонусы: вебинары из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ 14. Стереометрия. Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой — это первое видео раздела «Стереометрия», входящее в полный курс подготовки к ЕГЭ (о нем ниже).
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ №14. Стереометрия. Разбор варианта профильного ЕГЭ
Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
Об этом в нашем вебинаре в задаче о шестиугольной призме.
ЕГЭ 14 Стереометрия. Разбора задачи статграда, февраль 2021
Что проще: призма или пирамида? Хоть в призме и больше рёбер и граней, но с пирамидами справляться сложнее, причём прямо начиная с рисунка: все линии налезают друг на друга, ничего нигде не параллельно, в общем, лучше бы призму дали.
Но как только научились рисовать пирамиду, сразу всё стало проще: кругом одни треугольники, а как известно, фигур проще треугольника в геометрии найти не так-то просто :)
А если где прямые углы найдём, то вообще сказка.
Из этого видео вы узнаете, как правильно рисовать пирамиду и научитесь решать задачу №14 из февральского СтатГрада
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


