Дроби и действия с дробями
Что такое дроби?
Вспоминаются примеры из начальной школы. Представьте себе пирог вкусный такой, и 4 голодных ребенка.
Как бы им так сделать, чтоб пирога досталось всем? Верно, надо его поделить, поделить один пирог на 4 человека:
На рисунке ты видишь пирог, разрезанный на 4 дольки. Так вот, как раз дробь – это и есть доля от целого.
Сегодня мы разберем подробно, что такое дроби. Как их правильно делить, умножать, вычитать, складывать, преобразовывать…
В общем, сегодня ты узнаешь о дробях ВСЕ, что нужно знать для успешной сдачи ОГЭ или ЕГЭ.
Ну что, начнём? 🙂
Дроби — коротко о главном
Определения:
Простая дробь (обыкновенная дробь) – запись рационального числа в виде отношения двух чисел \(\displaystyle\frac{a}{b}\).
Делимое \(\displaystyle a\) – числитель дроби, а делитель \(\displaystyle b\) – знаменатель дроби.
Правильная дробь – дробь, у которой числитель меньше знаменателя.
Например: \(\displaystyle\frac{2}{5}\), \(\displaystyle\frac{1}{7}\) и так далее.
Неправильная дробь –дробь, у которой числитель больше или равен знаменателю.
Например: \(\displaystyle\frac{9}{5}\), \(\displaystyle\frac{13}{2}\) и так далее.
Смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
Например: \(\displaystyle2\frac{2}{5}\)\( \displaystyle \displaystyle=\frac{2\cdot 5}{5}+\frac{2}{5}=\frac{10}{5}+\frac{2}{5}=\frac{12}{5}\).
Десятичная дробь – обыкновенная дробь со знаменателем \(\displaystyle10\), \(\displaystyle100\), \(\displaystyle1000\) и так далее, (т.е. \(\displaystyle{{10}^{n}}\), где \(\displaystyle n\) — натуральное число).
Например: \(\displaystyle\frac{9}{100}\) в виде десятичной дроби записывается как \(\displaystyle0,09\),
\(\displaystyle\frac{225}{1000}\) записывается как \(\displaystyle0,225\).
Основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, дробь не изменится, несмотря на то, что выглядеть она будет по-другому.
Например: \(\displaystyle\frac{1}{5}=\frac{1\cdot 2}{5\cdot 2}=\frac{2}{10}\).
Действия с дробями:
Сложение/вычитание дробей
- две дроби с одинаковыми знаменателями: складываем/вычитаем их числители, а знаменатель оставляем без изменений: \(\displaystyle\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
- две обыкновенные дроби с разными знаменателями:
- приводим дроби к наименьшему общему знаменателю;
- складываем/вычитаем числители дробей, а знаменатель оставляем без изменений;
- сокращаем полученную дробь
- две смешанные дроби с разными знаменателями:
- приводим дробные части этих чисел к наименьшему общему знаменателю;
- по-отдельности складываем/вычитаем целые части и дробные части;
- если при сложении дробных частей получилась неправильная дробь, выделяем целую часть из этой дроби и прибавляем ее к полученной целой части / если дробная часть уменьшаемого меньше дробной части вычитаемого, превращаем ее в неправильную дробь, уменьшив на единицу, целую часть;
- сокращаем полученную дробь.
Умножение дробей
- умножение дроби на натуральное число: числитель умножаем на число, а знаменатель оставляем неизменным
- умножение двух обыкновенных дробей:
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь
- умножение двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем полученную дробь;
- если получилась неправильная дробь преобразовываем ее в смешанную.
Деление дробей
- деление дроби на натуральное число: знаменатель дроби умножаем на число, а числитель оставляем неизменным
- деление натурального числа на дробь: число умножаем на дробь обратную данной
- деление обыкновенных дробей: умножаем первую обыкновенную дробь на дробь, обратную второй
- деление двух смешанных чисел:
- преобразовываем смешанные дроби в неправильные;
- умножаем первую дробь на дробь, обратную второй; (3) сокращаем полученную дробь; (4) если получилась неправильная дробь преобразовываем ее в смешанную.
Сокращение дроби
Чтобы сократить дробь \(\displaystyle\frac{a}{b}\) нужно найти наибольший общий делитель ее числителя и знаменателя. Если наибольший общий делитель равен \(\displaystyle1\), то дробь сократить нельзя.
Например: \(\displaystyle\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}\).
Приведение дробей к наименьшему общему знаменателю
- найдите наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
- разделите наименьший общий знаменатель на знаменатели данных дробей, т. е. найдите для каждой дроби дополнительный множитель;
- умножьте числитель и знаменатели каждой дроби на ее дополнительный множитель.
Например: \(\displaystyle\frac{1}{3}\) и \(\displaystyle\frac{3}{4}\). Наименьший общий знаменатель — \(\displaystyle12\).
Дополнительный множитель первой дроби — \(\displaystyle12:3=4\), дополнительный множитель второй дроби — \(\displaystyle12:4=3\).
Следовательно: для первой дроби: \(\displaystyle\frac{1\cdot 4}{3\cdot 4}=\frac{4}{12}\), для второй дроби: \(\displaystyle\frac{3\cdot 3}{4\cdot 3}=\frac{9}{12}\).
Преобразования неправильной дроби в смешанную дробь
- поделите числитель дроби на ее знаменатель;
- остаток от деления запишите в числитель, знаменатель оставьте прежним;
- результат от деления запишите в качестве целой части.
Например: \(\displaystyle\frac{17}{4}\) = \(\displaystyle4\frac{1}{4}\).
Сравнение дробей:
- две дроби с одинаковыми знаменателями: больше та дробь, числитель которой больше
- две дроби с одинаковыми числителями: больше та дробь, знаменатель которой меньше
- две обыкновенные дроби: после приведения дробей к общему знаменателю, больше та дробь, числитель которой больше
Простые дроби
В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.
Это простая дробь.
Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac{1}{4}\), \(\displaystyle {1}/{4}\;.\)
Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).
Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).
Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)
То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.
Можно запомнить так: Ч – чердак. Числитель сверху 🙂
Примеры простых дробей: \(\displaystyle 1/5,\text{ }2/4,\text{ }3/10,\text{ }17/3.\)
Правильные и неправильные простые дроби
В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: \(\displaystyle 17/3\).
Если числитель больше знаменателя, то дробь называется неправильной.
Вне зависимости от того правильная дробь или неправильная, она будет простой.
Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?
Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?
Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.
А \(\displaystyle 17/3\)?
Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.
Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.
Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle 2\) куска.
А для целого пирога надо \( \displaystyle 3\) части. В итоге у нас \( \displaystyle 5\) целых и \( \displaystyle 2/3\) (две третьих) пирога.
Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle 5\frac{2}{3}\) (пять целых и две третьих).
Смешанная дробь
То, что у нас получилось (\( \displaystyle 5\frac{2}{3}\)), называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.
То, что между \( \displaystyle 5\) пирогами и \( \displaystyle 2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle 2x\)!!!
Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle 5\frac{2}{3}=5+\frac{2}{3}\).
Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь.
Ты же знаешь, как это сделать?
Преобразование из смешанной дроби в неправильную дробь.
Конечно, нужно умножить знаменатель дроби (в случае с , \(\displaystyle5\frac{2}{3}\) знаменатель равен \( \displaystyle 3\)), умножить знаменатель…, верно, на \(\displaystyle5\) и прибавить нецелую часть, а именно – \( \displaystyle 2\) .
В результате получим исходное \( \displaystyle 17/3\).
Преобразуй следующие неправильные дроби
- \( \displaystyle \frac{20}{10}\)
- \( \displaystyle \frac{19}{5}\)
- \( \displaystyle \frac{3}{2}\)
Ответы:
- \( \displaystyle \frac{20}{10}=2\)
- \( \displaystyle \frac{19}{5}=3\frac{4}{5}\)
- \( \displaystyle \frac{3}{2}=1\frac{1}{2}\)
Десятичные дроби
Существует еще один вид дробей, уверен ты его знаешь. Бери калькулятор и дели \( \displaystyle 11\) на \( \displaystyle 2\), например. Что пишет, \( \displaystyle 5,5\)? Что за штука такая?
Читается это как пять целых и пять десятых, равносильно \(\displaystyle5\frac{5}{10}\). Иными словами \( \displaystyle 11/2=5,5=5\frac{5}{10}\), все это одно и то же.
Дроби типа \( \displaystyle 5,5;\text{ }42,02;\text{ }0,122\) – все это десятичные дроби – это те же самые обыкновенные дроби, но в так называемой десятичной записи.
Десятичная запись используется для дробей со знаменателями \( \displaystyle 10\), \( \displaystyle 100\), \( \displaystyle 1000\) и т. д. В десятичных дробях так же есть целая и дробная части.
Для ясности возьмем вот такую дробь \( \displaystyle 12,856\):
- до запятой – целая часть (\( \displaystyle 12\));
- первый знак после запятой – десятые доли (\( \displaystyle 8/10\));
- второй – сотые доли (\( \displaystyle 5/100\));
- третий – (\( \displaystyle 6/1000\)).
И так далее. В зависимости от того на каком месте после запятой находится последний знак читается число. Читается так: \( \displaystyle 1,2\) – одна целая, две десятых; \( \displaystyle 42,02\)— сорок две целых, две сотых; \( \displaystyle 0,122\) – ноль целых сто двадцать две тысячных.
Преобразование десятичной дроби в обыкновенную дробь
Бывают ситуации, когда приходится преобразовывать десятичную дробь в обычную. Делается это очень просто.
Давай возьмем дробь \( \displaystyle 1,4\), например, запишем ее сначала как простую дробь, у нас будет ноль целых и четырнадцать десятых, так и напишем: \( \displaystyle 14/10\). Но дробь неправильная, ее можно сократить, а так же превратить в смешанную дробь:
\(\displaystyle\frac{14}{10}=\frac{7}{5}=1\frac{2}{5}\).
Сокращение дробей
Вот тебе дробь \( \displaystyle 4/6\) – при виде этой у тебя не возникает никаких мыслей? Ладно, давай так, и \( \displaystyle 4\) и \( \displaystyle 6\) делятся на… Да, делятся на \( \displaystyle 2\).
А что, если я скажу тебе, что ты можешь разделить \( \displaystyle 4\) на \( \displaystyle 2\) и разделить \( \displaystyle 6\) на \( \displaystyle 2\), и получившееся записать в таком виде как было до деления, а именно: \(\displaystyle\frac{4:2}{6:2}=\frac{2}{3}\), а проще говоря, \( \displaystyle 4/6=2/3\).
Это еще не все, ты так же можешь умножить на \( \displaystyle 3\), например, и \( \displaystyle 2\) и \( \displaystyle 3\), а результат записать так \(\displaystyle\frac{2\cdot 3}{3\cdot 3}=\frac{6}{9}\). По сути \(\displaystyle\frac{2}{3}=\frac{6}{9}\).
Все это вытекает из основного свойства дроби:
Если числитель и знаменатель дроби умножить (разделить) на одно и то же число, дробь не изменится.
С помощью основного свойства дроби можно заменить данную дробь другой, равной данной, но с меньшими числителем и знаменателем. Такая замена называется сокращением дроби.
Попробуй сократить дроби сам:
- \( \displaystyle 4/8\)
- \( \displaystyle 12/9\)
- \( \displaystyle 10/100\)
Ответы:
- \( \displaystyle 4/8=1/2\)
- \( \displaystyle 12/9=4/3\)
- \( \displaystyle 1/10\)
Приведение дробей к общему знаменателю
Представляешь, любые две дроби можно привести к общему знаменателю! Ну, если тебя это не поразило, ты, наверное, не понял о чем я. Вот смотри. Есть две дроби \( \displaystyle 1/3\) и \( \displaystyle 3/5\).
Тебе надо изменить эти дроби так, чтоб значение дробей не поменялось, но в знаменателе у обеих стало одно и то же число. Подскажу лишь, что для этого нужно воспользоваться основным свойством дроби.
Ладно, так и быть, покажу сам: \( \displaystyle 1/3=5/15\); \( \displaystyle 3/5=9/15\). Как ты видишь в знаменателе у обеих дробей \( \displaystyle 15\), и при этом, если сократить дроби, первую на \( \displaystyle 5\), а вторую на \( \displaystyle 3\), то получатся те же \( \displaystyle 1/3\) и \( \displaystyle 3/5\)!
Сказать, как это делается? Так и быть, тебе сегодня везет, читай ниже.
Алгоритм приведения дробей к общему знаменателю
- найти наименьшее общее кратное знаменателей этих дробей (наименьший общий знаменатель);
- разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
- умножить числитель и знаменатели каждой дроби на ее дополнительный множитель.
Наименьшим общим знаменателем (наименьшее общее кратное) этих двух дробей является \( \displaystyle 15\), то есть наименьшее число, которое делится и на \( \displaystyle 3\) и на \( \displaystyle 5\) (их знаменатели).
В данном случае я просто перемножил их знаменатели – умножил \( \displaystyle 3\) на \( \displaystyle 5\), получив тем самым \( \displaystyle 15\).
Чтоб понять этот момент лучше, советую обратиться к теме Целые числа, там ты найдешь, что такое наименьшее общее кратное (НОК) и с чем его едят.
Далее, по основному свойству дроби мне нужно было умножить числитель на то же число, на которое я домножал знаменатель, чтоб получить \( \displaystyle 15\). В первом случае это число \( \displaystyle 5\), во втором \( \displaystyle 3\).
И, наконец, найдя для обеих дробей множители, умножение на которые приведет к нужному результату, я умножаю и числитель и знаменатель дробей на соответствующие множители.
\(\displaystyle\frac{1\cdot 5}{3\cdot 5}=\frac{5}{15}\); \(\displaystyle\frac{3\cdot 3}{5\cdot 3}=\frac{9}{15}\)
Преобразование неправильной дроби в смешанную
- поделить числитель дроби на ее знаменатель;
- остаток от деления записать в числитель знаменатель оставить прежним;
- результат от деления записать в качестве целой части.
Потренируйся:
- \( \displaystyle 11/2\)
- \( \displaystyle 12/3\)
- \(\displaystyle213/15\)
Ответы:
- \( \displaystyle 11/2=5\frac{1}{2}\)
- \( \displaystyle 12/3=4\)
- \( \displaystyle 213/15=14\frac{3}{15}\)
Все дроби перебрали, а что с ними теперь делать-то? – спросишь ты. А тут, как и везде в математике, складывай, вычитай, умножай, дели – в общем, заняться есть чем!
Сложение дробей
Самый простой вариант, когда дроби, которые надо сложить, имеют одинаковый знаменатель.
Ты же еще не забыл, что это такое, правда?
Например, \( \displaystyle 2/5+1/5\). Вспомнив пример с кусочками пирога, думаю, ты без проблем догадаешься, что если складывать равные дольки одного пирога, то знаменатель меняться не будет, а складываются лишь числители.
Сложение будет выглядеть следующим образом: \( \displaystyle \frac{2}{5}+\frac{1}{5}=\frac{2+1}{5}=\frac{3}{5}\). Не сложно догадаться и как складывать смешанные дроби.
Отдельно складываются целые и дробные части:
\( \displaystyle 2\frac{2}{3}+4\frac{1}{3}=6\frac{2+1}{3}=6\frac{3}{3}=7\).
А что, если знаменатели у дробей разные, а? Например, \( \displaystyle 2/3+1/2\).
И тут ты сразу вспоминаешь, что мы проходили приведение дробей к общему знаменателю, и, наконец, становится понятно, зачем это было учить!
В данном примере общим знаменателем будет число \( \displaystyle 6\), как наименьшее общее кратное чисел \( \displaystyle 2\) и \( \displaystyle 3\). \( \displaystyle \frac{2}{3}+\frac{1}{2}=\frac{4}{6}+\frac{3}{6}=\frac{7}{6}=1\frac{1}{6}\).
Поскольку ты теперь умеешь приводить неправильную дробь к смешанной дроби, то открою тебе секрет, что это является не просто хорошим тоном, но и обязательным действием при упрощении выражений, после получения ответа избавиться от неправильных дробей.
С десятичными дробями все еще проще.
Сложение делается, как и с обычными числами, только не забывай про запятую. Вот тебе пример: \(\displaystyle15,2+2,91\).
Я предлагаю решать так: удобнее всего вычитать в столбик, расположив одну дробь под другой, но при этом запятая должна стоять строго под запятой вне зависимости от количества знаков до и после нее.
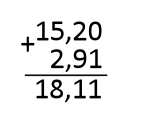
Как ты видишь, у второй дроби после запятой было на один знак больше. Для достижения одинакового количества знаков, я добавил еще один ноль в конце первой дроби.
Невероятно, но после последнего знака после запятой ты можешь добавить сколько угодно нулей, и это не изменит смысла дроби!
Вычитание дробей
Вычитание дробей практически ни чем не отличается от сложения, ну разве что знаком. А так, вычитается знаменатель из знаменателя, при сохранении общего числителя неизменным, а в случае если знаменатели разные, дроби приводятся к общему знаменателю.
Но куда же без специфики, тут она тоже присутствует.
Если ты вычитаешь одну смешанную дробь из другой, то в случае, если дробная часть уменьшаемой дроби меньше, чем у той, которую ты вычитаешь, то нужно уменьшить целую часть дроби на один и перенести в дробную часть, и вычитать из целой части целую, а из дробной дробную.
Что-нибудь понятно хоть чуточку? – Ладно, смотри пример, сейчас разберешься!
\( \displaystyle 4\frac{1}{3}-2\frac{2}{3}=3\frac{4}{3}-2\frac{2}{3}=1\frac{2}{3}\) – как ты видишь, в дробной части, тут из \( \displaystyle 1/3\) вычитается \( \displaystyle 2/3\).
Но, очевидно, что, не привлекая «кусочки» от целого пирога, вычитание совершить нельзя. Для этого один пирог режут на куски и добавляют их к дробной части.
Получается, что уже из \( \displaystyle 4/3\) вычитают \( \displaystyle 2/3\), а тут уж нет проблем.
А с десятичными дробями все то же самое, что и было при сложении.
Вот тебе пример:
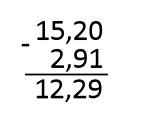
Есть вопросы по нему? Думаю, все логично и понятно, если нет, то еще раз посмотри, как делали сложение.
Умножение дробей
Умножать дробь на число — элементарно! \( \displaystyle 4\cdot \frac{2}{3}\ \) — вот пример, это произведение четырех и \( \displaystyle 2/3\), не путай с \( \displaystyle 4\frac{2}{3}\) — это четыре целых, две третьих!!! Ну, так вот, \( \displaystyle 4\cdot \frac{2}{3}\ =\frac{4\cdot 2}{3}=\frac{8}{3}=2\frac{2}{3}\).
Просто умножаешь число на числитель, а знаменатель не трогаешь!
Умножение смешанной дроби на число: \( \displaystyle 4\cdot 2\frac{2}{5}\) . Умножаешь и целую, и дробную части на \( \displaystyle 4\). Вот как это выглядит: \( \displaystyle 4\cdot 3\frac{2}{5}=12\frac{8}{5}=13\frac{3}{5}\).
Все сложнее при умножении дроби на дробь.
Алгоритм умножения дроби на дробь
- Если дробь смешанная, привести ее к виду обыкновенной неправильной дроби;
- Перемножить числители дробей, перемножить знаменатели дробей;
- Записать результат умножения числителей в числитель, а знаменателей, в знаменатель.
Заметь, что для умножения дробей с разными знаменателями не нужно приводить их к общему знаменателю!
Вот как все делается: \( \displaystyle 3\frac{2}{5}\cdot 2\frac{1}{3}=\frac{17}{5}\cdot \frac{7}{3}=\frac{119}{15}=7\frac{14}{15}\).
Умножение десятичных дробей на число или на десятичную дробь делается просто в столбик, и без запятых. Главное не забыть что?
Правильно, после умножения поставить запятую, отсчитав справа столько знаков, сколько было в сумме у двух множителей до умножения.
Например: \( \displaystyle 17,3\cdot 5,1=88,23\). В множителях было в сумме два знака справа от запятой, можно просто перемножить \( \displaystyle 173\) и \( \displaystyle 51\), а потом к результату дописать запятую, отсчитав два знака справа.
Деление дробей
Деление. А что деление? Деление это действие обратное умножению. Сейчас поясню, существует такое понятие, как «обратная дробь», или дробь обратная данной, иными словами, это попросту перевернутая дробь!
Деление дроби на дробь, по сути, это умножение на дробь обратную.
Смотри: \( \displaystyle \frac{1}{7}:\frac{3}{5}=\frac{1}{7}\cdot \frac{5}{3}=\frac{5}{21}\)
Как ты видишь, дробь \( \displaystyle 3/5\) просто переворачивается, а знак деления меняется на умножение!
А деление дроби на число или наоборот особо не отличается от деления на дробь, ведь любое число можно представить виде дроби – как, спросишь ты?
А ты знаешь, сколько будет \( \displaystyle 7/1\), например? По сути это \( \displaystyle 7\) пирогов разделить на одного человека. Сколько пирогов получит он? Семь!
Таким образом, любое число можно представить в виде дроби, в которой это число разделено на \(\displaystyle1\).
Значит, \( \displaystyle 7:\frac{3}{5}=\frac{7}{1}\cdot \frac{5}{3}=\frac{35}{3}=11\frac{2}{3}\).
Деление десятичных дробей производится ровно, так же как и умножение, с тем же главным правилом, не забывать после деления поставить в частном запятую, отсчитав справа столько знаков, сколько было в сумме у делимого и делителя до самого деления!
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


