Математические модели (ЕГЭ №10)

Математическая модель на практике

Задача 1

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время \( \displaystyle t\) падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле \( \displaystyle h=5{{t}^{2}}\), где — \( \displaystyle h\) расстояние в метрах, \( \displaystyle t\) — время падения в секундах.

До дождя время падения камешков составляло \( \displaystyle 0,5\) с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на \( \displaystyle 0,1\) с? Ответ выразите в метрах.

Решение:

О, ужас! Какие формулы, что за колодец, что происходит, что делать? Я прочел твои мысли?

Расслабься, в задачах этого типа условия бывают и пострашнее, главное помнить, что тебя в этой задаче интересуют формулы и отношения между переменными, а что все это обозначает в большинстве случаев не очень важно. Что ты тут видишь полезного?

Я лично вижу \( \displaystyle h=5{{t}^{2}}\).

Принцип решения этих задач следующий: берешь все известные величины и подставляешь. НО задумываться иногда надо!

Последовав моему первому совету и подставив все известные в уравнение, получим:

\( \displaystyle h=5\cdot {{0,5}^{2}}\)

\( \displaystyle h=1,25\)

Это я подставил время \( \displaystyle 0,5\) секунды, и нашел высоту \( \displaystyle h\), которую пролетал камень до дождя. А теперь надо посчитать после дождя и найти разницу!

Теперь прислушайся ко второму совету и задумайся, в вопросе уточняется, «на сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на \( \displaystyle 0,1\) с».

Сразу надо прикинуть, тааак, после дождя уровень воды повышается, значит, время падения камня до уровня воды меньше и тут витиеватая фраза «чтобы измеряемое время изменилось» приобретает конкретный смысл: время падения не увеличивается, а сокращается на указанные \( \displaystyle 0,1\) секунды.

Это означает, что в случае броска после дождя, нам просто нужно из начального времени \( \displaystyle 0,5\) c вычесть \( \displaystyle 0,1\) с, и получим уравнение высоты, которую камень пролетит после дождя:

\( \displaystyle h=5\cdot {{0,4}^{2}}\)

\( \displaystyle h=0,8\)

Ну и наконец, чтобы найти, на сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на \( \displaystyle 0,1\) с., нужно просто вычесть из первой высоты падения вторую!

\( \displaystyle 1,25-0,8=0,45\)

Получим ответ: на \( \displaystyle 0,45\) метра.

Как видишь, ничего сложного нет, главное, особо не заморачивайся, откуда такое непонятное и порой сложное уравнение в условиях взялось и что все в нем означает, поверь на слово, большинство этих уравнений взяты из физики, а там дебри похлеще, чем в алгебре.

Мне иногда кажется, что эти задачи придуманы, чтоб запугать ученика на ЕГЭ обилием сложных формул и терминов, а в большинстве случаев не требуют почти никаких знаний. Просто внимательно читай условие и подставляй известные величины в формулу!

Вот еще задача, уже не по физике, а из мира экономической теории, хотя знаний наук кроме математики тут опять не требуется.

Задача 2

Зависимость объёма спроса \( \displaystyle q\) (единиц в месяц) на продукцию предприятия-монополиста от цены \( \displaystyle p\) (тыс. руб.) задаётся формулой \( \displaystyle q=100-10p\). Выручка предприятия за месяц \( \displaystyle r\) (в тыс. руб.) вычисляется по формуле \( r(p)=q\cdot p\). Определите наибольшую цену \( \displaystyle p\), при которой месячная выручка \( \displaystyle r(p)\) составит не менее \( \displaystyle 240\) тыс. руб. Ответ приведите в тыс. руб.

Решение:

Угадай, что сейчас сделаю? Ага, начну подставлять то, что нам известно, но, опять же, немного подумать все же придется.

Пойдем с конца, нам нужно найти \( \displaystyle p\) при котором \( \displaystyle r(p)\ge 240\). Так, \( \displaystyle 240\) есть, равно какому-то \( \displaystyle r(p)\), находим, чему еще равно это \( \displaystyle r(p)\), а равно оно \( \displaystyle q\cdot p\), так и запишем \( \displaystyle q\cdot p=240\).

Как ты видишь, я особо не заморачиваюсь о смысле всех этих величин, просто смотрю из условий, что чему равно, так тебе поступать и нужно.

Вернемся к задаче, у тебя уже есть \( \displaystyle q\cdot p=240\), но как ты помнишь из одного уравнения с двумя переменными ни одну из них не найти, что же делать? Ага, у нас еще в условии осталась неиспользованная частичка \( \displaystyle q=100-10p\).

[thrive_lead_lock id=’9335′]

Вот, уже два уравнения и две переменных, значит, теперь обе переменные можно найти – отлично!

\( \displaystyle \left\{ \begin{array}{l}q\cdot p=240\\q=100-10p\end{array} \right.\)– такую систему решить сможешь?

Решаем подстановкой, у нас \( \displaystyle q\) уже выражена, значит, подставим ее в первое уравнение и упростим.

Получается вот такое квадратное уравнение: \( \displaystyle {{p}^{2}}-10p+24=0\), решаем, корни вот такие: 

\( \displaystyle {{p}_{1}}=6\), \( \displaystyle {{p}_{2}}=4\). 

В задании требуется найти наибольшую цену \( \displaystyle p\), при которой будут соблюдаться все те условия, которые мы учли, когда систему составляли. О, оказывается это \( \displaystyle p\) было ценой. Прикольно, значит, мы нашли цены: \( \displaystyle 6\) и \( \displaystyle 4\). Наибольшую цену, говорите? Окей, наибольшая из них, очевидно \( \displaystyle 6\), ее в ответ и пишем. Ну как, сложно? Думаю, нет, и вникать не надо особо!

А вот тебе и устрашающая физика, а точнее еще одна задачка:

Задача 3

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому \( \displaystyle P=\sigma S{{T}^{4}}\), где \( \displaystyle P\) — мощность излучения звезды, \( \displaystyle \sigma =-5,7\cdot {{10}^{-8}}\cdot \frac{Bт}{{{м}^{2}}\cdot {{K}^{\ 4}}}\) — постоянная, \( \displaystyle S\) — площадь поверхности звезды, а \( \displaystyle T\) — температура.

Известно, что площадь поверхности некоторой звезды равна \( \displaystyle \frac{1}{125}\cdot {{10}^{20}}{{M}^{2}}\), а мощность её излучения равна \( \displaystyle 4,56\cdot {{10}^{26}}\)Вт. Найдите температуру этой звезды в градусах Кельвина.

Решение:

Жуууть! Ищем подход. Я рекомендую для начала выписать себе на бумажке все формулы, которые ты тут видишь. Я вот в таком виде записал:

\( \displaystyle P=\sigma S{{T}^{4}}\)

\( \displaystyle \sigma =-5,7\cdot {{10}^{-8}}\cdot \frac{Bт}{{{м}^{2}}\cdot {{K}^{\ 4}}}\)

\( \displaystyle S=\frac{1}{125}\cdot {{10}^{20}}{{M}^{2}}\)

\( \displaystyle P=4,56\cdot {{10}^{26}}\)

\( \displaystyle T-?\)

Откуда \( \displaystyle S\) и \( \displaystyle P\) понятно? Да, в условии написано, что чему равно. Раньше я рекомендовал все неизвестные сразу подставлять, но здесь лучше сначала выразить неизвестное искомое \( \displaystyle T\).

Смотри как все просто: есть формула \( \displaystyle P=\sigma S{{T}^{4}}\) и в ней известны \( \displaystyle S\), \( \displaystyle P\) и \( \sigma \)(это греческая буква «сигма». Вообще, физики любят греческие буквы, привыкай).

А неизвестна температура \( \displaystyle T\). Давай выразим ее в виде формулы. Как это делать, надеюсь, знаешь? Такие задания на ГИА в 9 классе обычно дают:

.\( \displaystyle P=\sigma S{{T}^{4}}\text{ }\Rightarrow \text{ }{{T}^{4}}=\frac{P}{\sigma S}\text{ }\Rightarrow \text{ }T=\sqrt[4]{\frac{P}{\sigma S}}\)

Теперь осталось подставить числа вместо букв в правой части и упростить:

\( \displaystyle \begin{array}{l}T=\sqrt[4]{\frac{4,56\cdot {{10}^{26}}}{5,7\cdot {{10}^{-8}}\cdot \frac{1}{125}\cdot {{10}^{20}}}}=\sqrt[4]{\frac{4,56\cdot {{10}^{26}}}{5,7\cdot 0,008\cdot {{10}^{12}}}}=\sqrt[4]{\frac{456\cdot {{10}^{24}}}{456\cdot {{10}^{8}}}}=\\=\sqrt[4]{\frac{456\cdot {{10}^{16}}}{456}}=\sqrt[4]{{{10}^{16}}}={{10}^{4}}\end{array}\)

\( \displaystyle T=10000\)

Вот и ответ: \( \displaystyle 10000\) градусов Кельвина! А какая страшная была задача, а!

Продолжаем мучить задачки по физике.

Задача 4

Высота над землей подброшенного вверх мяча меняется по закону \( \displaystyle h(t)=1,6+8t-{{t}^{2}}\), где \( \displaystyle h\) — высота в метрах, \( \displaystyle t\) — время в секундах, прошедшее с момента броска.

Сколько секунд мяч будет находиться на высоте не менее трех метров?

Решение:

То были всё уравнения, а вот здесь надо определить, сколько мяч находился на высоте не менее трех метров, это значит на высоте \( \displaystyle \ge3\). Что мы составлять будем?

Неравенство, именно! У нас есть функция, которая описывает как летит мяч, где \( \displaystyle h(t)\) – это как раз та самая высота в метрах, нам нужна высота \( \displaystyle \ge3\). Значит,

\( a\text{ }=-12,5\)

\( b=125\)

\( {{T}_{0}}=\text{ }1450\)

\( {{T}_{max}}=\text{ }1750\)

\( t\text{ }-?\)

А теперь просто решаешь неравенство, главное, не забудь поменять знак неравенства с больше либо равно на меньше, либо равно, когда будешь умножать на \( \displaystyle -1\) обе части неравенства, чтоб перед \( \displaystyle {{t}^{2}}\) от минуса избавиться.

\( \displaystyle 1,6+8t-5{{t}^{2}}\ge 3\)

\( \displaystyle 5{{t}^{2}}-8t+1,4\le 0\)

\( \displaystyle {{t}_{1}}=0,2\)

\( \displaystyle {{t}_{2}}=1,4\)

Вот такие корни, строим интервалы для неравенства:

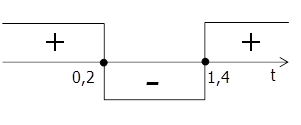
Нас интересует промежуток, где знак минус, поскольку неравенство принимает там отрицательные значения, это от \( \displaystyle 0,2\) до \( \displaystyle 1,4\) оба включительно.

А теперь включаем мозг и тщательно думаем: для неравенства мы применяли уравнение, описывающее полет мяча, он так или иначе летит по параболе, т.е. он взлетает, достигает пика и падает, как понять, сколько времени он будет находиться на высоте не менее \( \displaystyle 3\) метров?

Мы нашли 2 переломные точки, т.е. момент, когда он взмывает выше \( \displaystyle 3\) метров и момент, когда он, падая, достигает этой же отметки, эти две точки выражены у нас в виде времени.

То есть мы знаем на какой секунде полета он вошел в интересующую нас зону (выше \( \displaystyle 3\) метров) и в какую вышел из нее (упал ниже отметки в \( \displaystyle 3\) метра). Сколько секунд он находился в этой зоне?

Логично, что мы берем время выхода из зоны и вычитаем из него время вхождения в эту зону. Соответственно: \( \displaystyle 1,4\text{ }-\text{ }0,2=1,2~~\) — столько он находился в зоне выше \( \displaystyle 3\) метров, это и есть ответ.

Так уж тебе повезло, что больше всего примеров по этой теме можно взять из разряда задачек по физике, так что лови еще одну, она заключительная, так что поднапрягись, осталось совсем чуть-чуть!

Задача 5

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры от времени работы:

\( \displaystyle T\left( t \right)\text{ }=\text{ }{{T}_{0}}+\text{ }bt\text{ }+\text{ }a{{t}^{2}}\), где \( \displaystyle t\) — время в минутах, \( \displaystyle {{T}_{0}}=\text{ }1450\text{ }K\), \( \displaystyle a=-12,5\text{ }K/{{мин }^{2}}\), \( \displaystyle b=125\text{ }K/мин\).

Известно, что при температуре нагревательного элемента свыше \( \displaystyle 1750\ K\) прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Решение:

Действуем по отлаженной схеме, все, что дано, сперва выписываем:

\( \displaystyle a\text{ }=-12,5\)

\( \displaystyle b=125\)

\( \displaystyle {{T}_{0}}=\text{ }1450\)

\( \displaystyle {{T}_{max}}=\text{ }1750\)

\( \displaystyle t\text{ }-?\)

Теперь берем формулу и приравниваем ее к значению температуры, до которой максимально можно нагреть прибор пока он не сгорит, то есть \( \displaystyle {{T}_{max}}\):

\( \displaystyle {{T}_{0}}+\text{ }bt\text{ }+\text{ }a{{t}^{2}}={{T}_{max}}\)

Теперь подставляем вместо букв числа там, где они известны:

\( \displaystyle 1450+125t-12,5{{t}^{2}}=1750\)

\( \displaystyle 2,5{{t}^{2}}-25t-60=0\)

\( \displaystyle {{t}^{2}}-10t-24=0\)

\( \displaystyle {{x}_{1}}=6\)

\( \displaystyle {{x}_{2}}=4\)

Как видишь, температура при работе прибора описывается квадратным уравнением, а значит, распределяется по параболе, т.е. прибор нагревается до какой-то температуры, а потом остывает.

Мы получили ответы \( \displaystyle 4\) и \( \displaystyle 6\), следовательно, при \( \displaystyle 4\) и при \( \displaystyle 6\) минутах нагревания температура равна критической, но между \( \displaystyle 4\) и \( \displaystyle 6\) минутами — она еще выше предельной!

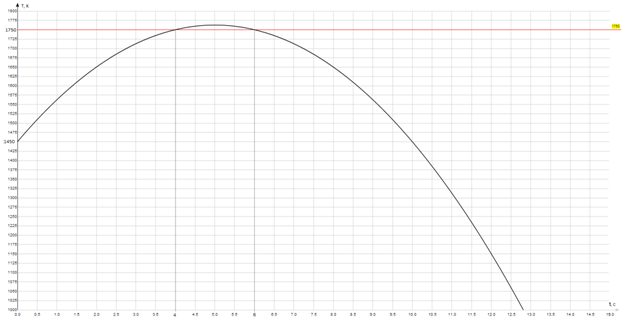
А значит, отключить прибор нужно через \( \displaystyle 4\) минуты.