Свойства степеней и действия с ними
Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?
Как обычно — чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ!
Чтобы узнать все о степенях и научиться пользоваться свойствами степеней, читай эту статью.
Поехали!
P.S Если ты хорошо знаешь степени и тебе надо только повторить, переходи сразу к продвинутому уровню.
НАЧАЛЬНЫЙ УРОВЕНЬ
Степени. Коротко о главном
Определение степени:
Степенью называется выражение вида: \( {{a}^{b}}\) , где: \( a\) — это основание, а \( b \) — это показатель степени.

Свойства степеней:
Произведение степеней с одинаковым основанием: | \( {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\) |
| Произведение степеней с одинаковыми показателями: | \( {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\) |
| Деление степеней с одинаковым основанием: | \( \frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}\) |
| Деление степеней с одинаковыми показателями: | \( \frac{{{a}^{n}}}{{{b}^{n}}}={{\left( \frac{a}{b} \right)}^{n}}\) |
| Возведение степени в степень: | \( {{\left( {{a}^{m}} \right)}^{n}}={{a}^{m\cdot n}}\) |
| Дробная степень: | \( {{a}^{\frac{n}{m}}}=\sqrt[m]{{{a}^{n}}}\) |
Особенности степеней:
- Отрицательное число, возведенное в четную степень, – число положительное;
- Отрицательное число, возведенное в нечетную степень, – число отрицательное;
- Положительное число в любой степени – число положительное;
- Ноль в любой степени равен \( 0\);
- Любое число в нулевой степени равно \( 1\);
- Степень с целым показателем — это степень, показатель которой натуральное число (т.е. целое и положительное);
- Степень с рациональным показателем — это степень, показатель которой отрицательные и дробные числа;
- Степень с иррациональным показателем — это степень, показатель которой бесконечная десятичная дробь или корень.
Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.
Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.
Сложение
\( 2+2+2+2+2+2+2+2=16 \)Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.
Умножение
Тот же самый пример с колой можно записать по-другому: \(\displaystyle 2\cdot 8=16\).
Математики — люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».
В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.
Согласись, \(\displaystyle 2\cdot 8=16\) считается легче и быстрее, чем \(\displaystyle 2+2+2+2+2+2+2+2=16\).
И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.
Круто, да?
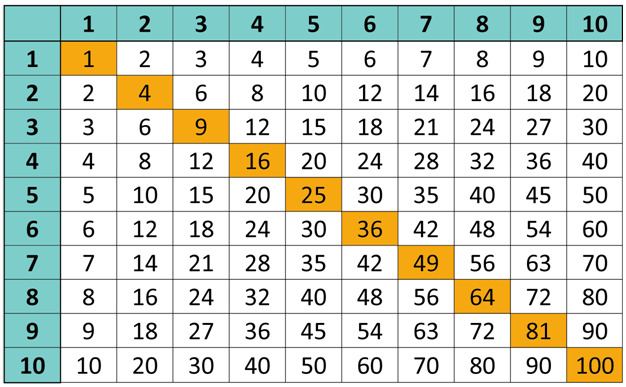
Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.

И другая таблица, красивее:
А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.
Возведение числа в степень
Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.
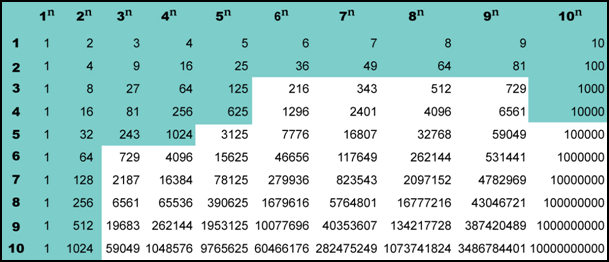
Например, \(\displaystyle 2\cdot 2\cdot 2\cdot 2\cdot 2={{2}^{5}}\). Математики помнят, что два в пятой степени – это \(\displaystyle 32\).
И решают такие задачки в уме – быстрее, легче и без ошибок.
Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.
Кстати, почему вторую степень называют квадратом числа, а третью — кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.
Примеры из жизни
Основание и показатель степени
Итак, для начала давай определим понятия. Как думаешь, что такое показатель степени? Это очень просто – это то число, которое находится «вверху» степени числа. Не научно, зато понятно и легко запомнить…
Ну и заодно, что такое основание степени? Еще проще – это то число, которое находится внизу, в основании.
Вот тебе рисунок для верности.

Ну и в общем виде, чтобы обобщить и лучше запомнить… Степень с основанием «\( \displaystyle a\) » и показателем «\( \displaystyle b\) » читается как «\( \displaystyle a\) в степени \( \displaystyle b\) » и записывается следующим образом:

Далее, почему говорят «степень числа с натуральным показателем»?
Ты уже наверное, догадался: потому что показатель степени – это натуральное число. Да, но что такое натуральное число? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?
Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам.
Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число \( \displaystyle 0\) . Ноль понять легко – это когда ничего нет.
А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне \( \displaystyle -100\) рублей, это значит, что ты должен оператору \( \displaystyle 100\) рублей.
Всякие дроби — это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа… Интересно, правда ведь?
Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число \( \displaystyle 3,141592…\).
Итак…
Натуральные, целые, рациональные и иррациональные числа это:
Натуральными называются числа, используемые при счете, то есть \( \displaystyle 1,\ 2,\ 3,\ 4\) и т.д;
Целыми – все натуральные числа, натуральные с минусом и число 0;
Рациональными считаются дробные числа;
Иррациональные числа – это бесконечная десятичная дробь.
Степень с натуральным показателем {n = 1, 2, 3,…}
Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
- Любое число в первой степени равно самому себе: \( \displaystyle {{a}^{1}}=a\)
- Возвести число в квадрат — значит умножить его само на себя: \( \displaystyle {{a}^{2}}=a\cdot a\)
- Возвести число в куб — значит умножить его само на себя три раза: \( \displaystyle {{a}^{3}}=a\cdot a\cdot a\)
Определение:
Возвести число в натуральную степень \( \displaystyle n\) — значит умножить число само на себя \( \displaystyle n\) раз:
\( \displaystyle {{a}^{n}}=\underbrace{a\cdot a\cdot a\cdot …a}_{n}\) .
Примеры:
- \( \displaystyle {{5}^{1}}=5\)
- \( \displaystyle {{4}^{3}}=4\cdot 4\cdot 4=16\cdot 4=64\)
- \( \displaystyle {{2}^{6}}=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2=64\)
Свойства степеней
Произведение степеней:
- \( \displaystyle {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\)
- \( \displaystyle {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\)
Деление степней:
- \( \displaystyle \frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}\)
- \( \displaystyle \frac{{{a}^{n}}}{{{b}^{n}}}={{\left( \frac{a}{b} \right)}^{n}}\)
Возведение степени в степень:
- \( \displaystyle {{\left( {{a}^{m}} \right)}^{n}}={{a}^{m\cdot n}}\)
Откуда взялись, например, первые два свойства? Сейчас покажу.
1. \( \displaystyle {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\)
Посмотрим: что такое \( \displaystyle {{a}^{n}}\) и \( \displaystyle {{a}^{m}}\) ?
По определению:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}\text{ }\end{array} \right|\Rightarrow \text{ }{{a}^{n}}\cdot {{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\cdot \underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}\text{ }\leftarrow \)Сколько здесь множителей всего?
Очень просто: к \( \displaystyle n\) множителям мы дописали \( \displaystyle m\) множителей, итого получилось \( \displaystyle n+m\) множителей.
Итак, в правой части этого выражения получается такое произведение:
\( \displaystyle {{a}^{n}}\cdot {{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{n+m\text{ множителей}}\)Но по определению это степень числа \( \displaystyle a\) с показателем \( \displaystyle n+m\) , то есть: \( \displaystyle {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\) , что и требовалось доказать.
Пример: Упростите выражение \( \displaystyle {{5}^{4}}\cdot {{5}^{7}}\cdot {{5}^{9}}\) .
Решение: \( \displaystyle {{5}^{4}}\cdot {{5}^{7}}\cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}\)
Пример: Упростите выражение \( \displaystyle {{3}^{5}}\cdot {{3}^{8}}\cdot {{5}^{7}}\) .
Решение:
Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!
Поэтому степени с основанием \( \displaystyle 3\) мы объединяем, а \( \displaystyle {{5}^{7}}\) остается отдельным множителем:
\( \displaystyle {{3}^{5}}\cdot {{3}^{8}}\cdot {{5}^{7}}={{3}^{5+8}}\cdot {{5}^{7}}={{3}^{13}}\cdot {{5}^{7}}\)Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нельзя написать, что \( \displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}\).
2. \( \displaystyle n\) -ая степень числа \( \displaystyle {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\)
Так же, как и с предыдущим свойством, обратимся к определению степени:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{b}^{n}}=\underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}\end{array} \right|\Rightarrow \text{ }{{a}^{n}}\cdot {{b}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\cdot \underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}\)Перегруппируем это произведение так:
\( \displaystyle {{a}^{n}}\cdot {{b}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\ множителей}\cdot \underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}=\underbrace{\left( a\cdot b \right)\cdot \left( a\cdot b \right)\cdot …\cdot \left( a\cdot b \right)}_{n\text{ множителей}}\)Получается, что выражение \( \displaystyle \left( a\cdot b \right)\) умножается само на себя \( \displaystyle n\) раз, то есть, согласно определению, это и есть \( \displaystyle n\) -ая степень числа \( \displaystyle \left( a\cdot b \right)\):
\( \displaystyle {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\), ч.т.д.
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме:
\( \displaystyle {{2}^{4}}+{{3}^{4}}\ne {{\left( 2+3 \right)}^{4}}\)!
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать \( \displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}\) ?
Но это неверно, ведь \( \displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\).
Степень с отрицательным основанием
До этого момента мы обсуждали только то, каким должен быть показатель степени.
Но каким должно быть основание?
В степенях с натуральным показателем основание может быть любым числом.
И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже \( \displaystyle 0\).
Давайте подумаем, какие знаки («\( \displaystyle +\)» или «\( \displaystyle —\)») будут иметь степени положительных и отрицательных чисел?
Например, положительным или отрицательным будет число \( \displaystyle {{3}^{5}}\)? А \( \displaystyle {{\left( -3 \right)}^{5}}\) ? \( \displaystyle {{\left( -3 \right)}^{4}}\)?
С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.
Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть \( \displaystyle \left( -3 \right)\cdot \left( -3 \right)=+9\) или \( \displaystyle {{\left( -3 \right)}^{2}}=9\). Но если мы \( \displaystyle 9\) умножим на \( \displaystyle \left( -3 \right)\), получится \( \displaystyle -27\).
И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:
Знаки степеней положительных и отрицательных чисел:
- Отрицательное число, возведенное в четную степень, – число положительное.
- Отрицательное число, возведенное в нечетную степень, – число отрицательное.
- Положительное число в любой степени – число положительное.
- Ноль в любой степени равен нулю.
Определи знак:
| 1) \( \displaystyle {{\left( 0,6 \right)}^{5}}\) | 2) \( \displaystyle {{\left( -4 \right)}^{5}}\) | 3) \( \displaystyle -{{\left( -\sqrt{3} \right)}^{6}}\) |
| 4) \( \displaystyle {{\left( -\frac{2}{5} \right)}^{4}}\) | 5) \( \displaystyle {{\left( 2-\sqrt{5} \right)}^{8}}\) | 6) \( \displaystyle {{\left( \sqrt{5}-3 \right)}^{7}}\) |
Справился?
Вот ответы: В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.
| 1) \( \displaystyle +\); | 2) \( \displaystyle —\); | 3) \( \displaystyle —\); |
| 4) \( \displaystyle +\); | 5) \( \displaystyle +\); | 6) \( \displaystyle —\). |
В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание – степень четная, а значит, результат всегда будет положительным.
Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно \( \displaystyle 0\) ? Очевидно нет, так как \( \displaystyle 2\ne \sqrt{5}\) (потому что \( \displaystyle 2=\sqrt{4}\) ).
Пример 6) уже не так прост!
Тут нужно узнать, что меньше: \( \displaystyle \sqrt{5}\) или \( \displaystyle 3\) ?
Если вспомнить, что \( \displaystyle 3=\sqrt{9}\) , становится ясно, что \( \displaystyle \sqrt{5}<3\) , а значит, основание меньше нуля.
То есть, применяем правило II: результат будет отрицательным.
6 примеров для тренировки:
1. \( \displaystyle \frac{{{3}^{4}}\cdot {{4}^{4}}}{{{12}^{3}}}\)
2. \( \displaystyle \frac{{{3}^{12}}\cdot {{3}^{41}}}{{{3}^{50}}}\)
3. \( \displaystyle \frac{{{\left( \frac{4}{7} \right)}^{8}}\cdot {{7}^{9}}}{{{4}^{7}}}\)
4. \( \displaystyle \frac{{{3}^{26}}}{{{\left( -3 \right)}^{35}}}\cdot {{\left( -6 \right)}^{10}}\)
5. \( \displaystyle {{\left( 2-\sqrt{5} \right)}^{8}}\cdot {{\left( \sqrt{5}+2 \right)}^{8}}\)
6. \( \displaystyle {{\left( \sqrt{7}-\sqrt{6} \right)}^{7}}\cdot \frac{{{\left( \sqrt{6}+\sqrt{7} \right)}^{5}}}{{{\left( \sqrt{6}-\sqrt{7} \right)}^{2}}}\)
Ответы:
Степень с целым показателем {0, ±1, ±2,…}
Целыми мы называем натуральные числа, противоположные им (то есть взятые со знаком «\( \displaystyle —\) ») и число \( \displaystyle 0\) .
Если показателем степени является целое положительное число, а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.
А теперь давайте рассмотрим новые случаи.
Начнем с показателя, равного \( \displaystyle 0\) .
\( \displaystyle {{a}^{0}}=1,\ a\ne 0\)Любое число в нулевой степени равно единице:
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием \( \displaystyle 3\). Возьмем, например \( \displaystyle {{3}^{5}}\), и домножим на \( \displaystyle {{3}^{0}}\):
\( \displaystyle {{3}^{5}}\cdot {{3}^{0}}\underset{\text{по правилу умножения}}{\mathop{=}}\,{{3}^{5+0}}={{3}^{5}}\)Итак, мы умножили число \( \displaystyle {{3}^{5}}\) на \( \displaystyle {{3}^{0}}\) и получили то же, что и было – \( \displaystyle {{3}^{5}}\). А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на \( \displaystyle 1\) . Значит \( \displaystyle {{3}^{0}}=1\) .
Можем проделать то же самое уже с произвольным числом \( \displaystyle a\):
\( \displaystyle {{a}^{n}}\cdot {{a}^{0}}\underset{по\ правилу \ умножения}{\mathop{=}}\,{{a}^{n+0}}={{a}^{n}}={{a}^{n}}\cdot 1\text{ }\Rightarrow \text{ }{{a}^{0}}=1\)Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть – это число \( \displaystyle 0\) (в качестве основания).
С одной стороны, \( \displaystyle 0\) в любой степени должен равняться \( \displaystyle 0\) – сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, \( \displaystyle {{0}^{0}}\) , как и любое число в нулевой степени, должен равняться \( \displaystyle 1\) . Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень.
То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа \( \displaystyle 0\) к целым относятся отрицательные числа.
Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
\( \displaystyle {{3}^{5}}\cdot {{3}^{-5}}\underset{\text{по правилу умножения}}{\mathop{=}}\,{{3}^{5+\left( -5 \right)}}={{3}^{5-5}}={{3}^{0}}=1\)Отсюда уже несложно выразить искомое \( \displaystyle {{3}^{-5}}\) :
\( \displaystyle {{3}^{5}}\cdot {{3}^{-5}}=1\text{ }\Rightarrow \text{ }{{3}^{-5}}=\frac{1}{{{3}^{5}}}\)Теперь распространим полученное правило на произвольную степень:
\( \displaystyle {{a}^{n}}\cdot {{a}^{-n}}={{a}^{n+\left( -n \right)}}={{a}^{0}}=1\text{ }\Rightarrow \text{ }{{a}^{-n}}=\frac{1}{{{a}^{n}}}\)Итак, сформулируем правило:
\( \displaystyle {{a}^{-n}}=\frac{1}{{{a}^{n}}},\ a\ne 0\) \( \displaystyle {{a}^{-n}}=\frac{1}{{{a}^{n}}},\ a\ne 0\) \( \displaystyle {{a}^{-n}}=\frac{1}{{{a}^{n}}},\ a\ne 0\)Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: \( \displaystyle a\ne 0\) (т.к. на \( \displaystyle 0\) делить нельзя).
Подведем итоги:
I. Выражение \( {{0}^{k}}\) не определено в случае \( k\le 0\) . Если \( k>0\) , то \( {{0}^{k}}=0\) .
II. Любое число в нулевой степени равно единице: \( \displaystyle {{a}^{0}}=1,\ a\ne 0\) .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: \( \displaystyle {{a}^{-n}}=\frac{1}{{{a}^{n}}},\ a\ne 0\).
\( \displaystyle {{6}^{-1}}=\frac{1}{6}\) \( \displaystyle {{\left( \frac{3}{2} \right)}^{-2}}=\frac{4}{9}\)6 примеров для тренировки
1. \( \displaystyle {{\left( -1 \right)}^{5}}\cdot \frac{6}{{{3}^{-4}}}\)
2. \( \displaystyle \frac{{{5}^{-2}}}{{{2}^{-5}}}\)
3. \( \displaystyle {{\left( -\frac{2}{3} \right)}^{-2}}\)
4. \( \displaystyle \frac{{{3}^{4}}\cdot {{3}^{-1}}+{{\left( -1,5 \right)}^{0}}}{{{2}^{-2}}}\)
5. \( \displaystyle {{\left( 6-4{{\left( \frac{3}{7} \right)}^{0}} \right)}^{-2}}\)
6. \( \displaystyle \frac{{{2}^{-3}}-{{\left( \frac{3}{4} \right)}^{-4}}{{\left( -\frac{1}{2} \right)}^{2}}}{{{10}^{-1}}+{{\left( -\frac{1}{5} \right)}^{0}}}\)
Решения:
Степень с рациональным показателем
Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.
Теперь рассмотрим рациональные числа. Какие числа называются рациональными?
Ответ: все, которые можно представить в виде дроби \( \displaystyle \frac{m}{n}\) , где \( \displaystyle m\) и \( \displaystyle n\) – целые числа, причем \( \displaystyle n\ne 0\) .
Чтобы понять, что такое «дробная степень», рассмотрим дробь \( \displaystyle \frac{1}{n}\) :
пусть \( \displaystyle {{3}^{\frac{1}{n}}}=x\) .
Возведем обе части уравнения в степень \( \displaystyle n\) :
\( \displaystyle {{\left( {{3}^{\frac{1}{n}}} \right)}^{n}}={{x}^{n}}\)Теперь вспомним правило про «степень в степени»:
\( \displaystyle {{x}^{n}}={{\left( {{3}^{\frac{1}{n}}} \right)}^{n}}={{3}^{\frac{1}{n}\cdot n}}={{3}^{1}}=3\)Какое число надо возвести в степень \( \displaystyle n\) , чтобы получить \( \displaystyle 3\) ?
Эта формулировка – определение корня \( \displaystyle n\) -ой степени.
Напомню: корнем \( \displaystyle n\) -ой степени числа \( \displaystyle a\) (\( \displaystyle \sqrt[n]{a}\) ) называется число, которое при возведении в степень \( \displaystyle n\) равно \( \displaystyle a\) .
То есть, корень \( \displaystyle n\) -ой степени – это операция, обратная возведению в \( \displaystyle n\) степень: \( \displaystyle \sqrt[n]{a}=b\text{ }\Leftrightarrow \text{ }a={{b}^{n}}\) .
Получается, что \( \displaystyle x={{3}^{\frac{1}{n}}}=\sqrt[n]{3}\) . Очевидно, этот частный случай можно расширить: \( \displaystyle {{a}^{\frac{1}{n}}}=\sqrt[n]{a}\) .
Теперь добавляем числитель: что такое \( \displaystyle {{a}^{\frac{m}{n}}}\) ? Ответ легко получить с помощью правила «степень в степени»:
\( \displaystyle {{a}^{\frac{m}{n}}}={{a}^{\frac{1}{n}\cdot m}}={{\left( {{a}^{\frac{1}{n}}} \right)}^{m}}={{\left( \sqrt[n]{a} \right)}^{m}}\) или \( \displaystyle \sqrt[n]{{{a}^{m}}}\) .
Но может ли основание \( \displaystyle a\) быть любым числом? Ведь корень можно извлекать не из всех чисел.
Например, можно ли посчитать число \( \displaystyle \sqrt[4]{-16}\) ? То есть, какое число нужно возвести в \( \displaystyle 4\) степень, чтобы получить \( \displaystyle -16\) ?
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень – число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение \( \displaystyle {{\left( -1 \right)}^{\frac{1}{2}}}\) не имеет смысла.
А что насчет выражения \( \displaystyle {{\left( -1 \right)}^{\frac{1}{3}}}\) ?
Его уже вроде бы можно посчитать: это \( \displaystyle \sqrt[3]{-1}=-1\) .
Но тут возникает проблема.
Число \( \displaystyle \frac{1}{3}\) можно представить в виде дргих, сократимых дробей, например, \( \displaystyle \frac{2}{6}\) или \( \displaystyle \frac{4}{12}\) .
И получается, что \( \displaystyle {{\left( -1 \right)}^{\frac{1}{3}}}\) существует, но \( \displaystyle {{\left( -1 \right)}^{\frac{2}{6}}}\) не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз \( \displaystyle \sqrt[3]{-8}=-2\) , то можно записать \( \displaystyle {{\left( -8 \right)}^{\frac{1}{3}}}=-2\) . Но стоит нам по-другому записать показатель, и снова получим неприятность: \( \displaystyle {{\left( -8 \right)}^{\frac{1}{3}}}={{\left( -8 \right)}^{\frac{2}{6}}}=\sqrt[6]{{{\left( -8 \right)}^{2}}}=\sqrt[6]{64}=2\) (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.
Итак, если:
- \( a>0\);
- \( m\) – натуральное число;
- \( n\) – целое число;
Тогда:
Примеры:
\( {{a}^{\frac{1}{2}}}=\sqrt{a}\)
\( {{a}^{\frac{1}{5}}}=\sqrt[5]{a}\)
\( {{a}^{-\frac{3}{4}}}=\frac{1}{\sqrt[4]{a^3}}\)
\( \displaystyle \frac{{{5}^{-\frac{1}{2}}}\cdot {{\left( {{5}^{\frac{5}{6}}} \right)}^{\frac{3}{10}}}\cdot {{3}^{-\frac{5}{4}}}}{{{3}^{-\frac{3}{2}}}}={{5}^{-\frac{1}{2}}}\cdot {{5}^{\frac{5}{6}\cdot \frac{3}{10}}}\cdot {{3}^{\left( -\frac{5}{4}+\frac{3}{2} \right)}}=\)
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
5 примеров для тренировки
- \( \displaystyle {{25}^{\frac{1}{5}}}\cdot {{125}^{\frac{1}{5}}}\)
- \( \displaystyle {{625}^{\frac{1}{4}}}\)z
- \( \displaystyle {{\left( \frac{4}{9} \right)}^{-\frac{1}{2}}}\)
- \( \displaystyle {{8}^{\frac{5}{3}}}\)
- \( \displaystyle \frac{{{3}^{\frac{2}{3}}}\cdot {{9}^{\frac{1}{2}}}\cdot {{27}^{-1}}}{{{3}^{-\frac{2}{3}}}\cdot {{\left( \frac{1}{3} \right)}^{^{\frac{3}{4}}}}\cdot {{\left( \frac{1}{9} \right)}^{-\frac{1}{24}}}}\)
Решения:
Степень с иррациональным показателем
Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением \( {{a}^{\frac{n}{m}}}=\sqrt[m]{{{a}^{n}}}\)
Ведь по определению иррациональные числа – это числа, которые невозможно представить в виде дроби \( \frac{m}{n}\) , где \( m\) и \( n\) – целые числа (то есть, иррациональные числа – это все действительные числа, кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем – это число, несколько раз умноженное само на себя; число в нулевой степени – это как-бы число, умноженное само на себя \( 0\) раз, то есть его еще не начали умножать, значит, само число еще даже не появилось – поэтому результатом является только некая «заготовка числа», а именно число \( 1\) ; степень с целым отрицательным показателем – это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель – это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например: \( {{3}^{\sqrt{2}}}\cdot {{3}^{1-\sqrt{2}}}={{3}^{\sqrt{2}+1-\sqrt{2}}}=3\)
Или: \( \frac{{{2}^{3\sqrt{3}}}}{{{8}^{\sqrt{3}-1}}}=\frac{{{2}^{3\sqrt{3}}}}{{{2}^{3\left( \sqrt{3}-1 \right)}}}={{2}^{3\sqrt{3}-3\sqrt{3}+3}}=8\)
И еще: \( {{\left( {{5}^{\sqrt[3]{4}}} \right)}^{\sqrt[3]{2}}}={{5}^{\sqrt[3]{8}}}={{5}^{2}}=25\).
3 примера для тренировки
- \( \displaystyle {{\left( {{5}^{\sqrt{3}-2}} \right)}^{2+\sqrt{3}}}\)
- \( \displaystyle {{\left( {{4}^{{{4}^{0,3}}}} \right)}^{{{4}^{\frac{1}{5}}}}}\)
- \( \displaystyle \frac{{{7}^{\sqrt{3}-2}}\cdot {{49}^{1-\sqrt{3}}}}{{{\left( \frac{1}{7} \right)}^{\sqrt{3}+1}}}\)
Решения
ПРОДВИНУТЫЙ УРОВЕНЬ
Продвинутый уровень предназначен для тех, кто уже хорошо знает степень и хотел бы быстро повторить.
Если вы такой (или такая), начинайте читать статью прямо отсюда.
Но если вам трудно или что-то не понятно возвращайтесь к начальному уровню.
Определение степени
Степенью называется выражение вида: \( {{a}^{b}}\), где \( a\) – основание степени и \( b\) – показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
- \( {{a}^{1}}=a\)
- \( {{a}^{2}}=a\cdot a\)
- \( {{a}^{3}}=a\cdot a\cdot a\)
Возвести число в натуральную степень n — значит умножить число само на себя \( n\) раз:
- \( {{a}^{n}}=\underbrace{a\cdot a\cdot a\cdot …a}_{n}\)
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
\( {{a}^{n}}={{a}^{n}},\ n>0\)Возведение в нулевую степень:
\( {{a}^{0}}=1,\ a\ne 0\) . \( {{0}^{0}}\) – выражение неопределенное, т.к., с одной стороны, \( 0\) в любой степени – это \( 0\) , а с другой – любое число в \( 0\) -ой степени – это \( 1\) .
Если показателем степени является целое отрицательное число:
\( {{a}^{-n}}=\frac{1}{{{a}^{n}}},\ a\ne 0\) (т.к. на \( 0\) делить нельзя).
Еще раз о нулях: выражение \( {{0}^{k}}\) не определено в случае \( k\le 0\). Если \( k>0\) , то \( {{0}^{k}}=0\) .
Примеры:
\( {{6}^{-1}}=\frac{1}{6}\) \( {{\left( \frac{3}{2} \right)}^{-2}}=\frac{4}{9}\)Степень с рациональным показателем
Если,
- \( a>0\);
- \( m\) – натуральное число;
- \( n\) – целое число;
Тогда:
- \( {{a}^{\frac{n}{m}}}=\sqrt[m]{{{a}^{n}}}\)
Примеры:
\( {{a}^{\frac{1}{2}}}=\sqrt{a}\) \( {{a}^{\frac{1}{5}}}=\sqrt[5]{a}\) \( {{a}^{-\frac{3}{4}}}=\frac{1}{\sqrt[4]{{{a}^{3}}}}\)Свойства степеней
| Произведение степеней | \( {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\) \( {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\) |
| Деление степеней | \( \frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}\) \( \frac{{{a}^{n}}}{{{b}^{n}}}={{\left( \frac{a}{b} \right)}^{n}}\) |
| Возведение степени в степень | \( {{\left( {{a}^{m}} \right)}^{n}}={{a}^{m\cdot n}}\) |
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Доказательства свойств степени
1. \( \displaystyle {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\)
Посмотрим: что такое \( \displaystyle {{a}^{n}}\) и \( \displaystyle {{a}^{m}}\) ?
По определению:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}\text{ }\end{array} \right|\Rightarrow \text{ }{{a}^{n}}\cdot {{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\cdot \underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}\)| Сколько здесь множителей всего? Очень просто: к \( \displaystyle n\) множителям мы дописали \( \displaystyle m\) множителей, итого получилось \( \displaystyle n+m\) множителей. |
Итак, в правой части этого выражения получается такое произведение:
\( \displaystyle {{a}^{n}}\cdot {{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{n+m\text{ множителей}}\)Но по определению это степень числа \( \displaystyle \mathbf{a}\) с показателем \( \displaystyle \mathbf{n}+\mathbf{m}\), то есть:
\( \displaystyle {{a}^{n}}\cdot {{a}^{m}}={{a}^{n+m}}\) , что и требовалось доказать.
Пример: Упростите выражение \( \displaystyle {{5}^{4}}\cdot {{5}^{7}}\cdot {{5}^{9}}\) .
Решение: \( \displaystyle {{5}^{4}}\cdot {{5}^{7}}\cdot {{5}^{9}}={{5}^{4+7+9}}={{5}^{20}}\) .
Пример: Упростите выражение \( \displaystyle {{3}^{5}}\cdot {{3}^{8}}\cdot {{5}^{7}}\) .
Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием \( \displaystyle 3\) мы объединяем, а \( \displaystyle {{5}^{7}}\) остается отдельным множителем:
\( \displaystyle {{3}^{5}}\cdot {{3}^{8}}\cdot {{5}^{7}}={{3}^{5+8}}\cdot {{5}^{7}}={{3}^{13}}\cdot {{5}^{7}}\) .
Еще одно важное замечание: это правило – только для произведения степеней!
Ни в коем случае нелья написать, что \( \displaystyle {{2}^{4}}+{{2}^{6}}={{2}^{10}}\) .
2. \( \displaystyle {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\)
Так же, как и с предыдущим свойством, обратимся к определению степени:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{b}^{n}}=\underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}\end{array} \right|\Rightarrow \text{ }{{a}^{n}}\cdot {{b}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\cdot \underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}\) .
Перегруппируем это произведение так:
\( \displaystyle {{a}^{n}}\cdot {{b}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\cdot \underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}=\underbrace{\left( a\cdot b \right)\cdot \left( a\cdot b \right)\cdot …\cdot \left( a\cdot b \right)}_{n\text{ множителей}}\).
Получается, что выражение \( \displaystyle a\cdot b\) умножается само на себя \( \displaystyle n\) раз, то есть, согласно определению, это и есть \( \displaystyle n\) -я степень числа \( \displaystyle a\cdot b\) :
\( \displaystyle {{a}^{n}}\cdot {{b}^{n}}={{\left( a\cdot b \right)}^{n}}\), ч.т.д.
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: \( \displaystyle {{2}^{4}}+{{3}^{4}}\ne {{\left( 2+3 \right)}^{4}}\) !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать \( \displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}\) ? Но это неверно, ведь \( \displaystyle {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\) .
3. \( \displaystyle \frac{{{a}^{n}}}{{{a}^{m}}}={{a}^{n-m}}\)
И снова используем определение степени:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{a}^{m}}=\underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}\text{ }\end{array} \right|\Rightarrow \text{ }\frac{{{a}^{n}}}{{{a}^{m}}}=\frac{\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}}{\underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}}\)| Здесь, очевидно, можем сократить. Но с одной оговоркой: чтобы степень получилась натуральная, нам придется предположить, что \( \displaystyle n>m\) (то есть, в числителе множителей должно быть больше, чем в знаменателе). Тогда \( \displaystyle m\) множителей числителя сокращаются со всеми \( \displaystyle m\) множителями знаменателя. Таким образом множители остаются только в числителе, причем в количестве \( \displaystyle n-m\) штук: |
\( \displaystyle \frac{{{a}^{n}}}{{{a}^{m}}}=\frac{\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}}{\underbrace{a\cdot a\cdot …\cdot a}_{m\text{ множителей}}}=\frac{\underbrace{a\cdot a\cdot …\cdot a}_{n-m\text{ множителей}}}{1}={{a}^{n-m}}\) , ч.т.д.
4. \( \displaystyle \frac{{{a}^{n}}}{{{b}^{n}}}={{\left( \frac{a}{b} \right)}^{n}}\)
Все как обычно – записываем определение степеней \( \displaystyle {{a}^{n}}\) и \( \displaystyle {{b}^{n}}\) , делим их друг на друга, разбиваем на пары \( \displaystyle \frac{a}{b}\) и получаем:
\( \displaystyle \left. \begin{array}{l}{{a}^{n}}=\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}\\{{b}^{n}}=\underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}\end{array} \right|\Rightarrow \text{ }\frac{{{a}^{n}}}{{{b}^{n}}}=\frac{\underbrace{a\cdot a\cdot …\cdot a}_{n\text{ множителей}}}{\underbrace{b\cdot b\cdot …\cdot b}_{n\text{ множителей}}}=\underbrace{\frac{a}{b}\cdot \frac{a}{b}\cdot …\cdot \frac{a}{b}}_{n\text{ множителей}}={{\left( \frac{a}{b} \right)}^{n}}\) , ч.т.д.
Прежде чем разобрать последнее правило, решим несколько примеров.
6 примеров для тренировки
Вычисли значения выражений:
- \( \displaystyle \frac{{{3}^{4}}\cdot {{4}^{4}}}{{{12}^{3}}}\)
- \( \displaystyle \frac{{{3}^{13}}\cdot {{3}^{41}}}{{{3}^{50}}}\)
- \( \displaystyle \frac{{{\left( \frac{4}{7} \right)}^{8}}\cdot {{7}^{9}}}{{{4}^{7}}}\)
- \( \displaystyle \frac{{{3}^{26}}}{{{\left( -3 \right)}^{35}}}\cdot {{\left( -6 \right)}^{10}}\)
- \( \displaystyle {{\left( 2-\sqrt{5} \right)}^{8}}\cdot {{\left( \sqrt{5}+2 \right)}^{8}}\)
- \( \displaystyle {{\left( \sqrt{7}-\sqrt{6} \right)}^{7}}\cdot \frac{{{\left( \sqrt{6}+\sqrt{7} \right)}^{5}}}{{{\left( \sqrt{6}+\sqrt{7} \right)}^{2}}}\)
Решения:
1. \( \displaystyle \frac{{{3}^{4}}\cdot {{4}^{4}}}{{{12}^{3}}}=\frac{{{\left( 3\cdot 4 \right)}^{4}}}{{{12}^{3}}}=\frac{{{12}^{4}}}{{{12}^{3}}}={{12}^{4-3}}=12.\)
2. \( \displaystyle \frac{{{3}^{13}}\cdot {{3}^{41}}}{{{3}^{50}}}=\frac{{{3}^{12+41}}}{{{3}^{50}}}={{3}^{53-50}}={{3}^{3}}=27.\)
3. \( \displaystyle \frac{{{\left( \frac{4}{7} \right)}^{8}}\cdot {{7}^{9}}}{{{4}^{7}}}=\frac{\frac{{{4}^{8}}}{{{7}^{8}}}\cdot {{7}^{9}}}{{{4}^{7}}}=\frac{{{4}^{8}}\cdot {{7}^{9}}}{{{7}^{8}}\cdot {{4}^{7}}}=\frac{{{4}^{8}}}{{{4}^{7}}}\cdot \frac{{{7}^{9}}}{{{7}^{8}}}=4\cdot 7=28.\)
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org




Спасибо, Алексей, за доступное, бодрое изложение.
Вот бы Вы написали нам новые учебники!!!!!!!!!
Учить и учиться было бы намного веселей и продуктивней!!!
Спасибо, Валерия Валерьевна. Очень приятно слышать.
Спасибо вам за отзыв! Думаю, можете давать ученикам ссылку на наш учебник, может быть и им понравится:)
Добрый вечер. Подскажите пожалуйста почему у меня в некоторых местах нет решения?
Елена, здравствуйте! Чтобы видеть все скрытые ччасти текста, зарегистрируйтесь (для этого нажмите синюю кнопку Регистрация или перейдите по ссылке https://youclever.org/?ff_landing=22 ).
Если вы уже зарегистрированы, но что-то не отображается, попробуйте обновить кэш страницы — нажмите комбинацию CTRL+F5.
Если это не поможет, напишите мне на почту alexey.shevchuk@youclever.org
пример номер 6
из «6 примеров для тренировки» ошибка в знаменателе дроби
в задании сумма корней (SQRT(6)+SQRT(7))^2
в решении в _разность_ (SQRT(6)-SQRT(7))^2
имеется ввиду задание в последнем разделе «продвинутый уровень «
Цитата: «Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем.
Итак, если:
a>0;
n – натуральное число;
m – целое число;
Тогда:
a в степени n/m = …»
У Вас как минимум в двух местах механическая опечатка. В том виде, как записана формула, допускается деление на целое число — ноль.
Надо исправить; здесь m — натуральное число, а n — целое число.
Очень хорошие уроки. Огромное спасибо за Ваш труд!
Спасибо большое, Андрей и за отзыв и за то, что заметили ошибку (за ошибку в особенности). Удачи на всех экзаменах!
Некоторые комментарии прошлых лет к этой статье:
Денис
28 февраля 2018
Большое спасибо за разъяснения, все бы так учили давно бы космос покорили.
Александр (админ)
28 февраля 2018
Спасибо, Денис. Будем покорять )
Маша
15 апреля 2019
Не понимаю, куда дели (-1)^35 в 4м примере продвинутого раздела. Это должно быть -1. Куда дальше делся минус?
Алексей Шевчук
11 мая 2019
Маша, минус дальше пишем перед всем выражением.
Денис
24 июня 2019
Спасибо за этот сайт
Александр (админ)
24 июня 2019
Пожалуйста, Денис! Приятно слышать.
Александр
18 сентября 2019
Очень классно объясняете. Буду отправлять на ваш сайт младшую сестру:) У меня есть задачка по степеням из программирования. Нужно выяснить что больше: a в степени b или b в степени a. Есть ли какие-то свойства для степеней, которые могли бы помочь решить данную задачу без возведения в степени?
Алексей Шевчук
18 сентября 2019
Спасибо, Александр! Можно, например, прологарифмировать оба выражения по основанию a (или b, это не важно) и посмотреть, что больше: b или a*log_a(b). Скорость вычисления логарифма сравнима с возведением в маленькую степень (до 10), но для больших чисел выигрыш во времени существенный.
Сергей
13 октября 2019
Спасибо огромное, разъяснено добротно только хочется видеть в столбик все свойства степеней
Александр (админ)
14 октября 2019
Сергей, спасибо за совет. Как раз собираюсь обновить учебник. Сделать его еще более читабельным.
Иоанн
04 февраля 2020
Спасибо! Сдаю академ. задолженность за 8 класс, за день учу всё, что не учил целый год! Всё описано ясно и чётко, по человечески!
Александр (админ)
04 февраля 2020
Очень приятно слышать! Желаю вам сдать все на отлично! Все в ваших руках.