Двугранный угол
Привет!
Дай нам 10 минут ты разберешься в одной из самых важных тем стереометрии.
И получишь за неё баллы на ЕГЭ!
Поехали!
Двугранный угол — коротко о главном
Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.
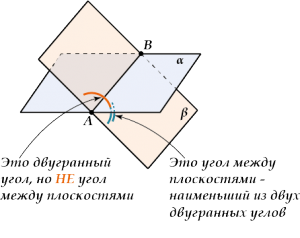
Двугранный угол может быть и острым и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!
- Двугранный угол измеряется величиной своего линейного угла.
- Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90{}^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90{}^\circ \).
Два способа найти угол между плоскостями:
- При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
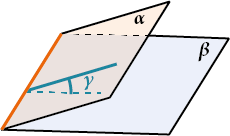
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
\( \displaystyle \cos \gamma =\frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\)
Двугранный угол — определения
Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
Вот так:
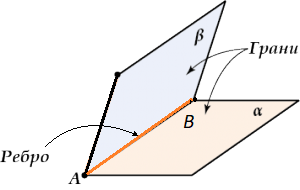
При этом прямая \( \displaystyle AB\) – это ребро двугранного угла, а полуплоскости \( \displaystyle \alpha \) и \( \displaystyle \beta \) – стороны или грани двугранного угла.
Двугранный угол получает обозначение по своему ребру: «двугранный угол \( \displaystyle AB\)».
С понятием двугранного угла тесно связано понятие угол между плоскостями.
Угол между плоскостями – наименьший из двугранных углов, образованных при пересечении плоскостей.

Итак, внимание! Различие между двугранным углом и углом между плоскостями в том, что:
Двугранный угол может быть и острым, и тупым, а угол между плоскостями только острым! НЕ ПУТАЙ!
Линейный угол двугранного угла
Как измерить двугранный угол?
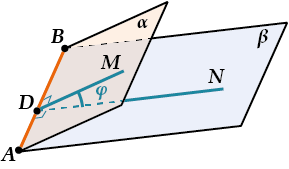
Нужно поступить так: из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру.
Смотри:

В плоскости \( \displaystyle \alpha \) провели перпендикуляр \( \displaystyle MD\) к ребру \( \displaystyle AB\). Что получилось? Обычный, плоский угол \( \displaystyle \varphi \).
Вот этот угол и называется: линейный угол двугранного угла \( \displaystyle AB\).
Зачем этот линейный угол? Запомни, это очень ВАЖНО:
Двугранный угол измеряется величиной своего линейного угла.
То есть математически договорились, что если угол φ будет равен, к примеру \( \displaystyle 20{}^\circ \), то это будет автоматически означать, что угол \( \displaystyle AB\) равен \( \displaystyle 20{}^\circ \).
Вот и ключ к поиску величины двугранного угла и угла между плоскостями:
Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
Ещё раз немного о названиях.
Прямой двугранный угол – двугранный угол, который равен \( \displaystyle 90{}^\circ \), то есть тот, у которого линейный угол равен \( \displaystyle 90{}^\circ \).
Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.

Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Вот такая:
| \( \displaystyle \cos \gamma =\frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\) |
Здесь \( \displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}\) — коэффициенты уравнений плоскостей \( \displaystyle \alpha \) и \( \displaystyle \beta \) соответственно.
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
\( \displaystyle \alpha \): \( \displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0\)
\( \displaystyle \beta \): \( \displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0\).
Какой же способ лучше? Зависит от задачи.
Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать \( \displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}\), а потом ещё и \( \displaystyle \cos \gamma \).
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.
Решение геометрическим способом
В правильной треугольной пирамиде боковое ребро в три раза больше ребра основания. Найти двугранный угол при основании пирамиды.
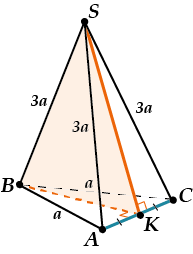
Решение алгебраическим способом (метод координат)
В правильной треугольной пирамиде боковое ребро в три раза больше ребра основания. Найти двугранный угол при основании пирамиды.
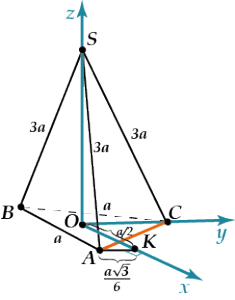
Введём систему координат с центром в центре основания, \( \displaystyle Ox\parallel AB\); \( \displaystyle Oy\) вдоль \( \displaystyle OC\), \( \displaystyle Oz\) — вдоль высоты пирамиды.
Тогда плоскость \( \displaystyle ABC\) имеет уравнение \( \displaystyle z=0\), то есть \( \displaystyle {{A}_{1}}=0\), \( \displaystyle {{B}_{1}}=0\), \( \displaystyle {{C}_{1}}=1\).
Найдём уравнение плоскости \( \displaystyle SAC\).
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
На этом уроке на примере самых простых объемных фигур мы научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Куб, параллелепипед и призма — задача №8 из ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Статья хорошая и даже очень! Спасибо
Спасибо, Серый! Нам всем приятно!