Формулы сокращенного умножения
Зачем нужны формулы сокращенного умножения?
С их помощью ты сможешь упростить выражение, привести многочлен к стандартному виду (без раскрытия скобок и приведения подобных)
Ты сможешь легко в уме находить квадраты больших чисел и, например, быстро проверить свои расчеты на экзамене.
Иными словами это сильно экономит время при решении самых разных задач!
В общем их стоит выучить. Начнем?
Формулы сокращенного умножения — коротко о главном
Формулы сокращенного умножения – это формулы, зная которые можно избежать выполнения некоторых стандартных действий при упрощении выражений или разложении многочленов на множители.

Формулы сокращенного умножения нужно знать наизусть!
Квадрат суммы
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения:
\( \displaystyle {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\)
Название «Формулы сокращенного умножения» совсем не случайно, потому что эти формулы позволяют сократить время на умножение. Вот смотри…
Возьмем самую простую первую формулу квадрата суммы \( {{\left( a+b \right)}^{2}}\) — и попробуем возвести сумму в скобках в квадрат, то есть, умножить \( \left( a+b \right)\) само на себя:
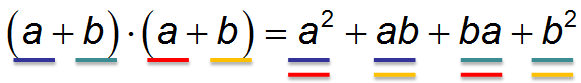
Приведи подобные слагаемые и ты получишь формулу сокращенного умножения квадрат суммы:
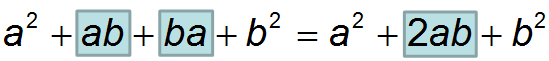
Таким образом выводятся все формулы сокращенного умножения.
Ты можешь выводить их каждый раз самостоятельно, а можешь не тратить на это время и быстро посчитать необходимый пример, зная конечное значение формул.
Конечно, квадрат суммы посчитать вручную не так сложно, но что ты скажешь насчет куба суммы или куба разности?
Куб суммы означает, что необходимо \( \left( a+b \right)\) само умножить на себя три раза:
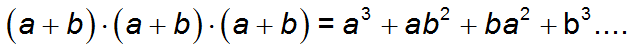
И это мы расписали перемножение только первой скобки, а тоже самое необходимо сделать со второй и с третьей… Согласись, запутаться очень легко, а, как правило, от того, как ты посчитаешь это простое действие, зависит ответ всего примера.
Таким образом, формулы сокращенного умножения позволяют сократить трудоемкое перемножение членов друг на друга и получить быстрый результат.
Как выводится формула для квадрата суммы, мы описали ранее. Попробуем произвести аналогичные действия с квадратом разности.
Квадрат разности
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения:
\( \displaystyle {{(a-b)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\)
Квадрат разности означает умножить \( \left( a-b \right)\) само на себя. Попробуй вывести формулу для данного выражения самостоятельно, по аналогии с квадратом суммы.
Справился? Посмотрим, как ты раскрыл скобки:
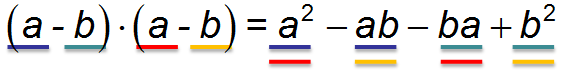
Что мы делаем дальше? Правильно, приводим подобные слагаемые:
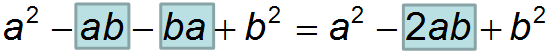
Ты наверняка уже заметил некую закономерность? Присмотрись внимательно к формулам квадрат суммы и квадрат разности. В чем их отличие?
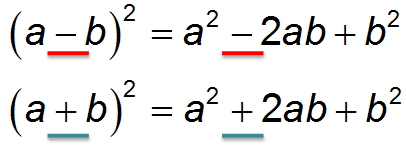
Конечно, ты увидел, что если мы возводим в квадрат разность между \( a\) и \( b\), то мы вычитаем их удвоенное произведение, а если возводим в квадрат сумму, то прибавляем.
При возведении разности и суммы в квадрат, не забывай про удвоенное произведение чисел \( a\) и \( b\)!
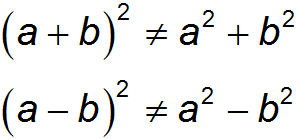
Это грубейшая и самая распространенная ошибка!
Попробуй таким способом вычислить следующие выражения:
- \( {{102}^{2}}\);
- \( {{119}^{2}}\);
- \( {{151}^{2}}\).
Ответы:
Посчитай самостоятельно выражения:
- \( {{(2b+3c)}^{2}}\);
- \( {{(b+4a)}^{2}}\);
- \( {{(12-5a)}^{2}}\).
Ответы:
Соберем формулу из вида \( {{a}^{2}}\pm 2ab+{{b}^{2}}\) в вид \( {{\left( a\pm b \right)}^{2}}\)
Подведем небольшой итог и запишем формулы квадрата суммы и разности в одну строку:
\( {{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}\)Теперь потренируемся «собирать» формулу из разложенного вида \( {{a}^{2}}\pm 2ab+{{b}^{2}}\) в вид \( {{\left( a\pm b \right)}^{2}}\). Данный навык понадобится нам в дальнейшем при преобразовании больших выражений.
Допустим, у нас есть следующее выражение:
\( 16+24b+9{{b}^{2}}\).
Мы знаем, что квадрат суммы (или разности) – это квадрат одного числа \( +\) квадрат другого числа и \( \pm \) удвоенное произведение этих чисел.
В данной задаче легко увидеть квадрат одного числа – это \( 9{{b}^{2}}\). Соответственно, одно из чисел, входящих в скобку \( {{\left( a\pm b \right)}^{2}}\) , — это квадратный корень из \( 9{{b}^{2}}\), то есть
\( {{\left( 3b \right)}^{2}}=9{{b}^{2}}\)Так как во втором слагаемом есть \( b\), значит, это удвоенное произведение одного и другого числа, соответственно:
\( 24b=2\cdot 3b\cdot x\), где \( \displaystyle x\) – второе число, входящее в нашу скобку.
\( x=\frac{24b}{6b}=4\). Второе число, входящее в скобку, равно \( \displaystyle 4\).
Проверим. \( \displaystyle 16\) должно быть равно \( {{4}^{2}}\). Действительно, так и есть, значит, мы нашли оба числа, присутствующие в скобках: \( 4\) и \( 3b\). Осталось определить знак, который стоит между ними. Как ты думаешь, что за знак там будет?
Правильно! Так как мы прибавляем удвоенное произведение, то между числами будет стоять знак сложения. Теперь запиши преобразованное выражение. Справился? У тебя должно получиться следующее:
\( 16+24b+9{{b}^{2}}={{\left( 4+3b \right)}^{2}}\)Заметь: перемена мест слагаемых не сказывается на результате (неважно, сложение или вычитание стоит между \( a\) и \( b\)).
\( 16+24b+9{{b}^{2}}={{\left( 4+3b \right)}^{2}}={{\left( 3b+4 \right)}^{2}}\)Совершенно необязательно, чтобы слагаемые в преобразуемом выражении стояли так, как написано в формуле.
Посмотри на это выражение: \( 12b+9+4{{b}^{2}}\). Попробуй преобразовать его самостоятельно. Получилось?
\( 12b+9+4{{b}^{2}}=2\cdot 3\cdot 2b+{{3}^{2}}+{{\left( 2b \right)}^{2}}={{\left( 2b+3 \right)}^{2}}\)Потренируйся – преобразуй следующие выражения:
- \( 16{{b}^{2}}-8b+1\);
- \( 25+4{{a}^{2}}+20a\);
- \( -42c+9{{c}^{2}}+49\).
Ответы:
Справился? Закрепим тему.
Выбери из приведенных ниже выражений те, которые можно представить в виде квадрата суммы или разности.
- \( 4{{b}^{2}}-8b+9\);
- \( 25+9{{a}^{2}}+30a\);
- \( 9{{a}^{2}}+81-54a\).
Ответы:
Разность квадратов
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
\( \displaystyle {{a}^{2}}-{{b}^{2}}=(a-b)(a+b)\)
Еще одна формула сокращенного умножения – разность квадратов.
Разность квадратов — это не квадрат разности!
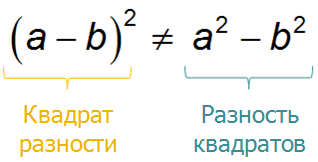
Разность квадратов двух чисел равна произведению суммы этих чисел на их разность
Проверим, верна ли эта формула. Для этого перемножим \( \left( a-b \right)\left( a+b \right)\), как делали при выведении формул квадрата суммы и разности:
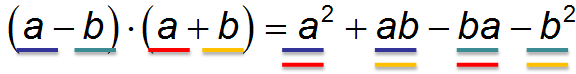
Что мы делаем дальше? Правильно! Приводим подобные слагаемые и получаем:
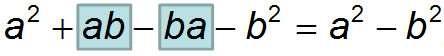
Таким образом, мы только что удостоверились, что формула действительно верная. Данная формула также упрощает сложные вычислительные действия.
Приведем пример:
Необходимо вычислить: \( {{145}^{2}}-{{45}^{2}}\). Конечно, мы можем возвести в квадрат \( 145\), затем возвести в квадрат \( 45\) и вычесть одно из другого, но формула упрощает нам задачу:
\( {{145}^{2}}-{{45}^{2}}=\left( 145-45 \right)\cdot \left( 145+45 \right)=100\cdot 190=19000\)Попробуй самостоятельно посчитать следующие выражения:
- \( {{135}^{2}}-{{15}^{2}}\);
- \( {{200}^{2}}-{{180}^{2}}\);
- \( {{19}^{2}}-{{6}^{2}}\).
Получилось? Сверим результаты:
Так же, как и квадрат суммы (разности), формула разности квадратов может применяться не только с числами:
\( {{\left( 3a \right)}^{2}}-{{7}^{2}}=\left( 3a-7 \right)\cdot \left( 3a+7 \right)\)Умение раскладывать разность квадратов поможет нам преобразовывать сложные математические выражения.
Обрати внимание:
\( {{\left( 3a \right)}^{2}}-{{7}^{2}}\ne 3{{a}^{2}}-{{7}^{2}}\)Поскольку \( 3={{\left( \sqrt{3} \right)}^{2}}\), при разложении на квадрат разности правого выражения мы получим
\( 3{{a}^{2}}-{{7}^{2}}={{\left( a\sqrt{3} \right)}^{2}}-{{7}^{2}}=\left( a\sqrt{3}-7 \right)\left( a\sqrt{3}+7 \right)\).
Будь внимателен и смотри, какое конкретное слагаемое возводится в квадрат!
Для закрепления темы преобразуй следующие выражения:
- \( 49{{a}^{2}}-{{b}^{2}}\);
- \( 3{{a}^{2}}-5\);
- \( {{(5a)}^{2}}-3\);
- \( {{(9a)}^{2}}-81\).
Записал? Сравним полученные выражения:
Теперь, когда ты усвоил квадрат суммы и квадрат разности, а также разность квадратов, попробуем решать примеры на комбинацию этих трех формул.
Квадрат суммы, квадрат разности, разность квадратов — задачи на комбинацию этих формул
Упростите выражение:
\( \frac{9{{a}^{2}}+{{b}^{2}}+6ab}{\left( 3a+b \right)\left( 3a-b \right)}\).
Посмотри внимательно, что ты видишь в числителе? Правильно, числитель — это полный квадрат:
\( \frac{9{{a}^{2}}+{{b}^{2}}+6ab}{\left( 3a+b \right)\left( 3a-b \right)}=\frac{{{\left( 3a+b \right)}^{2}}}{\left( 3a+b \right)\left( 3a-b \right)}=\frac{\left( 3a+b \right)}{\left( 3a-b \right)}\)Упрощая выражение, помни, что подсказка, в какую сторону двигаться в упрощении, находится в знаменателе (или в числителе).
В нашем случае, когда знаменатель разложен, и больше ничего сделать нельзя, можно понять, что числителем будет либо квадрат суммы, либо квадрат разности.
Так как мы прибавляем \( 6ab\), то становится ясно, что числитель – квадрат суммы.
Попробуй самостоятельно преобразовать следующие выражения:
\( \frac{64{{a}^{2}}-36}{64{{a}^{2}}+36-96}\);
\( \frac{\left( 4a+2b \right)\left( 4a-2b \right)}{16{{a}^{2}}+4{{b}^{2}}-16ab}\);
\( \frac{\left( 2a+3c \right)\left( 2a-3c \right)}{4{{a}^{2}}-9{{c}^{2}}}\).
А теперь сверь результаты:
Куб суммы и куб разности
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения:
\( \displaystyle {{(a+b)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\)
\( \displaystyle {{(a-b)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\)Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения:
Формулы куба суммы и куба разности выводятся аналогичным образом, как квадрат суммы и квадрат разности: раскрытием скобок при перемножении членов друг на друга.
Если квадрат суммы и квадрат разности запомнить весьма легко, то возникает вопрос «как запомнить кубы?»
Посмотри внимательно на две описываемые формулы в сравнении с возведением аналогичных членов в квадрат:
| \( {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\) | \( {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\) |
| \( {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\) | \( {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\) |
Какую ты видишь закономерность?
- При возведении в квадрат у нас есть квадрат первого числа и квадрат второго. При возведении в куб – есть куб одного числа и куб другого числа.
- При возведении в квадрат, у нас есть удвоенное произведение чисел (числа в 1 степени, что на одну степень меньше чем та, в которую возводим выражение). При возведении в куб – утроенное произведение, при котором одно из чисел возводится в квадрат (что так же на 1 степень меньше, чем степень, в которую возводим выражение).
- При возведении в квадрат знак в скобках в раскрытом выражении отражается при прибавлении (или вычитании) удвоенного произведения – если в скобках сложение, то прибавляем, если вычитание – отнимаем. При возведении в куб правило такое: если у нас куб суммы, то все знаки «+», а если куб разности, то знаки чередуются: «\( +\)» — «\( —\)» — «\( +\)» — «\( —\)».
Всё перечисленное, кроме зависимости степеней при умножении членов, изображено на рисунке.
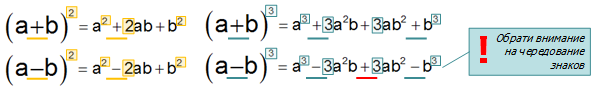
Потренируемся? Раскрой скобки в следующих выражениях:
- \( {{(4a+2)}^{3}}\);
- \( {{(2b-4)}^{3}}\);
- \( {{(3c+1)}^{3}}\);
- \( {{(5a+2b)}^{3}}\).
Сравни полученные выражения:
Разность и сумма кубов
\( \displaystyle {{a}^{3}}-{{b}^{3}}=(a-b)({{a}^{2}}+ab+{{b}^{2}})\)Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений:
\( \displaystyle {{a}^{3}}+{{b}^{3}}=(a+b)({{a}^{2}}-ab+{{b}^{2}})\)Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений:
Рассмотрим последнюю пару формул разность и сумму кубов.
Как мы помним, в разности квадратов у нас идет перемножение разности и суммы данных чисел одно на другое. В разности кубов и в сумме кубов также имеется две скобки:
\( {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\);
\( {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\).
1 скобка – разность (или сумма) чисел в первой степени (в зависимости от того, разность или сумму кубов мы раскрываем);
2 скобка – неполный квадрат (присмотрись: если бы мы вычитали (или прибавляли) удвоенное произведение чисел, был бы квадрат), знак при перемножении чисел противоположный знаку изначального выражения.
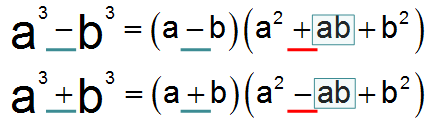
Для закрепления темы решим несколько примеров:
- \( {{(3a)}^{3}}-1\);
- \( {{(4c)}^{3}}+125\);
- \( 8{{a}^{3}}-{{b}^{3}}\);
- \( {{(3a)}^{3}}-{{(2b)}^{3}}\);
- \( 64{{a}^{2}}-1\);
- \( {{(3a+2c)}^{3}}\);
- \( {{\left( 60+1 \right)}^{2}}\);
- \( {{97}^{2}}\);
- \( \frac{{{48}^{2}}-{{22}^{2}}}{{{79}^{2}}-{{51}^{2}}}\);
Упростите выражение (двумя способами): \( {{\left( x-y \right)}^{2}}-{{\left( x+y \right)}^{2}}\).
Сравни полученные выражения:
Доказательство формул сокращенного умножения
1. \( {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\).
Возвести выражение в квадрат — значит умножить его само на себя:
\( {{\left( a+b \right)}^{2}}=\left( a+b \right)\left( a+b \right)\).
Раскроем скобки и приведем подобные:
\( {{\left( a+b \right)}^{2}}=\left( a+b \right)\left( a+b \right)={{a}^{2}}+\underline{ab}+\underline{ba}+{{b}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\).
2. \( {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\).
Делаем то же самое: умножаем разность саму на себя, раскрываем скобки и приводим подобные:
\( {{\left( a-b \right)}^{2}}=\left( a-b \right)\left( a-b \right)={{a}^{2}}-\underline{ab}-\underline{ba}+{{b}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\).
3. \( {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\).
Возьмем выражение в правой части и раскроем скобки:
\( \left( a-b \right)\left( a+b \right)={{a}^{2}}+\underline{ab}-\underline{ba}-{{b}^{2}}={{a}^{2}}-{{b}^{2}}\).
4. \( {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\).
Число в кубе можно представить как это число умноженное на свой квадрат:
\( \displaystyle {{\left( a+b \right)}^{3}}={{\left( a+b \right)}^{2}}\cdot \left( a+b \right)=\underbrace{\left( {{a}^{2}}+2ab+{{b}^{2}} \right)}_{квадрат\ суммы}\left( a+b \right)=\)
\( \displaystyle={{a}^{3}}+\underline{{{a}^{2}}b}+\underline{2{{a}^{2}}b}+\underline{\underline{2a{{b}^{2}}}}+\underline{\underline{{{b}^{2}}a}}+{{b}^{3}}=\)
\( \displaystyle={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\)
5. \( \displaystyle {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\)
Аналогично:
\( \displaystyle {{\left( a-b \right)}^{3}}={{\left( a-b \right)}^{2}}\cdot \left( a-b \right)=\underbrace{\left( {{a}^{2}}-2ab+{{b}^{2}} \right)}_{\text{квадрат}\ \ разности}\left( a-b \right)=\)
\( \displaystyle {{a}^{3}}-\underline{{{a}^{2}}b}-\underline{2{{a}^{2}}b}+\underline{\underline{2a{{b}^{2}}}}+\underline{\underline{{{b}^{2}}a}}-{{b}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\)
В разности кубов знаки чередуются.
6. \( {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\).
Раскроем скобки в правой части:
\( \left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)={{a}^{3}}-\underline{{{a}^{2}}b}+\underline{\underline{a{{b}^{2}}}}+\underline{{{a}^{2}}b}-\underline{\underline{a{{b}^{2}}}}+{{b}^{3}}={{a}^{3}}+{{b}^{3}}\).
7. \( {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\).
Раскроем скобки в правой части:
\( \left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)={{a}^{3}}+\underline{{{a}^{2}}b}+\underline{\underline{a{{b}^{2}}}}-\underline{{{a}^{2}}b}-\underline{\underline{a{{b}^{2}}}}-{{b}^{3}}={{a}^{3}}-{{b}^{3}}\).
Как с помощью формул сокращенного умножения считать в уме
У тебя есть квадратная комната 103 на 103 метра и тебе нужно застелить ее плитками метр на метр. Сколько нужно плиток? Продавец – твой друг – говорит, что тебе нужно «около 12000 плиток».
Проверять его расчеты тебе не удобно, но ты можешь посчитать в уме! С помощью формул сокращенного умножения.
Просто представь 103, как сумму 100 и 3 и возведи ее в квадрат:
\( \displaystyle {{103}^{2}}={{\left( 100+3 \right)}^{2}}={{100}^{2}}+2\cdot 100\cdot 3+{{3}^{2}}=10000+600+9=10609 \)
Смекаешь?
С помощью формул сокращенного умножения можно легко в уме находить квадраты больших чисел.
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Формулы сокращенного умножения — разбор 119 примеров
Эти формулы нужны для задачи №9 – на преобразование выражений. Также они нужны для решения уравнений и неравенств, очень часто пригождаются в задачах №13 и 15.
А в 18 задаче без них вообще нечего делать.
Цель этого видео в том, чтобы вы тему «Формулы сокращенного умножения» закрыли полностью, чтобы научились решать любую задачу на ЕГЭ.
Если смотреть вебинар времени нет, посмотри для начала видео о самом сложном навыке, касающемся формул сокращенного умножения- о выделении полного квадрата.
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Алексей, спасибо. Просьба прокомментировать свойства формул: (a-b)^2n = (b-a)^2n
Виктория, любая чётная степень работает как модуль: всё отрицательное делает положительным. Поэтому, как знаки в скобках не меняй — всё равно плюс выйдет. Вот отсюда и это свойство:)
Огромная благодарность
Спасибо и вам, Валерий!
просто огонь, шикарно, я очень благодарен за такое понятное и доступное объяснение, уважаю и люблю) Спасибо за ваш труд!
Спасибо большое, Дамир4ик. Очень приятно слышать. Заходите еще )