Многоугольники
Привет!
Никогда не было интересно, почему в треугольнике 180 градусов?
А в других фигурах сколько? Да постой, положи транспортир!
Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.
Поехали!
Многоугольники — коротко о главном
Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle {{A}_{1}},\text{ }{{A}_{2}},\text{ }…,~{{A}_{n}}\) и соединить их последовательно отрезками.
- Точки \( \displaystyle {{A}_{1}},~{{A}_{2}},\text{ }…,~{{A}_{n}}\) — вершины многоугольника.
- Отрезки \( \displaystyle {{A}_{1}}{{A}_{2}},~\ {{A}_{2}}{{A}_{3}},\text{ }…,\text{ }{{A}_{n}}{{A}_{1}}\) – стороны многоугольника.
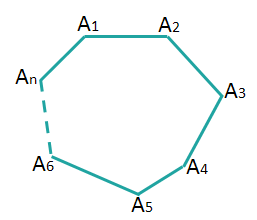
Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.
Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.
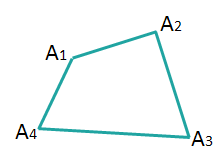
Четырехугольник
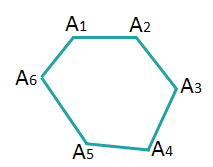
Шестиугольник
Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.
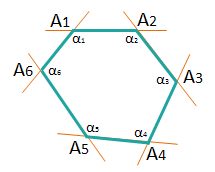
Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180{}^\circ \cdot (n-2)\) или \( \displaystyle {{\alpha }_{1}}+{{\alpha }_{2}}+\text{ }…~+{{\alpha }_{n}}\), где \( \displaystyle {{\alpha }_{n}}\) – внутренний угол многоугольника.
Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.
Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac{n-2}{n}\cdot 180{}^\circ \).
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.
Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac{{{A}_{1}}{{A}_{2}}+{{A}_{2}}{{A}_{3}}+…+{{A}_{n}}{{A}_{1}}}{2}\).
Многоугольник — подробнее
Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle {{A}_{1}},\text{ }{{A}_{2}},\text{ }…,~{{A}_{n}}\) и соединить их последовательно отрезками.
- Точки \( \displaystyle {{A}_{1}},~{{A}_{2}},\text{ }…,~{{A}_{n}}\) — вершины многоугольника.
- Отрезки \( \displaystyle {{A}_{1}}{{A}_{2}},~\ {{A}_{2}}{{A}_{3}},\text{ }…,\text{ }{{A}_{n}}{{A}_{1}}\) – стороны многоугольника.

При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).
Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.
Произвольные многоугольники
Давай-ка нарисуем, какие бывают многоугольники.
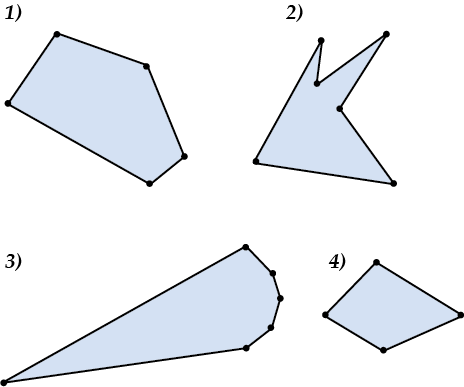
А теперь вопрос: какой из этих многоугольников выпадает из ряда?
Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?
Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.
Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.
Итак, основной факт:
В любом многоугольнике сумма внутренних углов равна \( \displaystyle 180^o(n-2)\), где буква «\( \displaystyle n\)» означает число углов многоугольника.
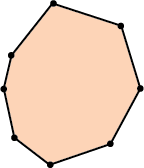
Давай сразу к примерам:
Четырехугольник
\( \displaystyle 180^\circ\left( 4-2 \right)=360{}^\circ \)
Пятиугольник
\( \displaystyle 180^\circ\left( 5-2 \right)=540{}^\circ \)
Шестиугольник
\( \displaystyle 180^\circ\left( 6-2 \right)=720{}^\circ \)
Ах да, про треугольник забыли.
Треугольник
\( \displaystyle 180^\circ\left( 3-2 \right)=180{}^\circ \)
Сумма углов многоугольника. Доказательство.
А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).
Зачем?
Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.
Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.
Итак, давай разделим многоугольник на треугольники.
Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:
Всего вершин: \( \displaystyle n\)
Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:
- Самой вершины B
- Вершины A
- Вершины C
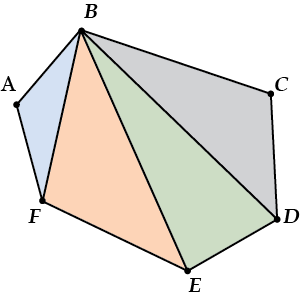
Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?
Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.
Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.
Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180{}^\circ \).
Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180{}^\circ \), значит:
Сумма углов многоугольника равна \( \displaystyle 180{}^\circ \)\( \displaystyle (n-2)\)
Вот и доказали.
Что же из этого может оказаться полезным? Два момента:
Правильные многоугольники
Многоугольник называется правильным, если все его углы и все его стороны равны.
Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.
Первый вопрос:
А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?
И ответ: можно!
Давай посмотрим на примере.
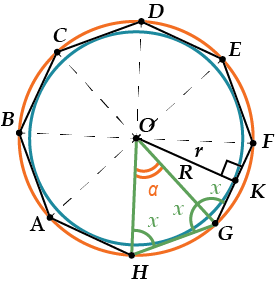
Пусть есть, скажем, правильный восьмиугольник:
Сумма всех его углов равна \( \displaystyle 180{}^\circ \left( 8-2 \right)=1080{}^\circ \).
А сколько всего углов? Восемь конечно, и они все одинаковые.
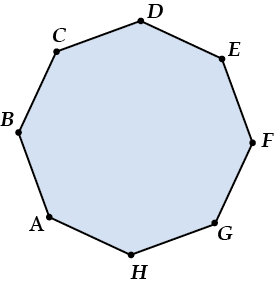
Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:
\( \displaystyle \angle A=\frac{1080{}^\circ }{8}=135{}^\circ \).
Что мы еще должны знать?
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
При этом центры этих окружностей совпадают.
Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.
Давай опять на примере восьмиугольника.
Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)
Значит, \( \displaystyle \frac{r}{R}=\sin \angle x\) – и это не только в восьмиугольнике!
Чему же равен в нашем случае \( \displaystyle \angle x\)?
Ровно половине \( \displaystyle \angle G\), представь себе!
Значит \( \displaystyle \angle x=\frac{135{}^\circ }{2}=67,5{}^\circ \).
Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac{r}{R}=\sin 67,5{}^\circ \).
Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?
И тот же ответ: конечно можно!
Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).
И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.
Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник
Даша, например, можно провести отрезок из вершины в середину противоположной стороны.
Некоторые комментарии прошлых лет к этой статье:
Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.
Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.
Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!
Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!
Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)
Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.