Описанный четырехугольник
Сегодня ты узнаешь некоторые теоремы, которые помогут тебе в решении, казалось бы, сложных задач по геометрии.
Но после прочтения этой статьи они станут легкими!
Ведь ты будешь знать все об описанном четырехугольнике!
Поехали!
Коротко о главном
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
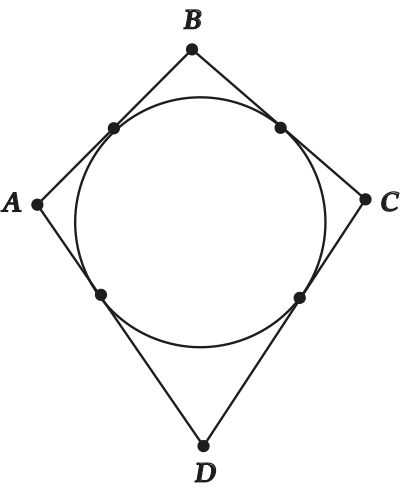
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
В буквах: \( \large AB+CD=AD+BC\)
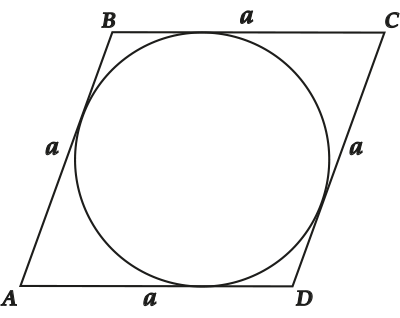
Если в параллелограмм можно вписать окружность, то это – ромб.
Что такое описанный четырехугольник
Посмотри — сперва нарисуем:

А теперь напишем:
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
А что, разве не всегда существует такая окружность?
Ведь вон треугольник-то всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.
Представь себе, например, длинный прямоугольник.

Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.
А в какие же можно? Вот, оказывается есть такая теорема (утверждение то есть).
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Вот как это записывается в буквах:
\( \displaystyle a+c=b+d\)
или (то же самое)
\( \displaystyle AB+CD=AD+BC\)
Для лучшего понимания давай в буквальном смысле разберём на кусочки описанный четырехугольник. Смотри: пусть в четырехугольнике ???????????????? «сидит» окружность.

Но тогда у нас есть огромное количество касательных! Ты ещё помнишь, что отрезки касательных, проведённых из одной точки, равны? Ну, вот, значит
\( \displaystyle BK=BN\) (обозначим \( \displaystyle x\))
\( \displaystyle CK=CL\) (обозначим \( \displaystyle y\))
\( \displaystyle DL=DM\) (обозначим \( \displaystyle z\))
\( \displaystyle AM=AN\) (обозначим \( \displaystyle u\))
А теперь получилось, что
\( \displaystyle \left| \begin{array}{l}AB=x+u\\CD=y+z\end{array} \right.\Rightarrow AB+CD=x+y+z+u\)
и
\( \displaystyle \left| \begin{array}{l}BC=x+y\\AD=u+z\end{array} \right.\Rightarrow BC+AD=x+y+z+u\)
То есть \( \displaystyle AB+CD=AD+BC\)! Здорово, правда?
А теперь получим простое, но красивое следствие из этой теоремы.
Следствие. Если в параллелограмм можно вписать окружность, то это ромб.
Почему? Давай разберёмся. Пусть есть параллелограмм \( \displaystyle ABCD\).
Раз параллелограмм, то \( \displaystyle AB=CD,~AD=BC\) (вспоминаем свойства параллелограмма). Обозначим \( \displaystyle \text{AB}=\text{CD}\) буквой \( \displaystyle a\), а \( \displaystyle \text{AD}=\text{BC}\) буквой \( \displaystyle b\).
А теперь применим теорему. \( \displaystyle ABCD\) описанный \( \displaystyle \Rightarrow a+a=b+b\), то есть \( \displaystyle a=b\) – вот и получился ромб.

Видишь, как сработала теорема?
Вот и ты, если видишь в задачке надпись «в четырёхугольник вписана окружность» или, конкретнее, скажем, «в трапецию вписана окружность», то сразу вспоминай, что \( \displaystyle AB+CD=AD+BC\), – и задача решится!
Ну… или не сразу решится, но этот факт непременно тебе поможет.
Доказательство теоремы об окружности, вписанной в четырехугольник

Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
Давай прежде всего осознаем, что, в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.
Ну, вот пример:

А раз так, то математики, конечно же, не могли успокоиться, пока не придумали теорему, которая сообщит нам, что же такое нужно требовать от четырехугольника, чтобы в него можно было поместить окружность, касающуюся всех сторон.
И вот эта теорема:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

В буквах:
\( \large a+c=b+d\)
или (в других буквах)
\( \large AB+CD=AD+BC\)
Заметь, что (как всегда) слова «тогда и только тогда» означают сразу два утверждения: «туда» и «обратно». Итак, если подробнее, то теорема утверждает:
(Вспоминаем Алису с безумным шляпником и их «ем то, что вижу» и «вижу то, что ем»)
А теперь – доказательство!
Пункт 1 вообще ОЧЕНЬ лёгкий. Смотри:

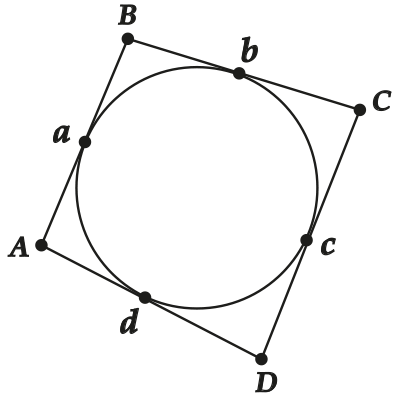
Пусть в \( ABCD\) вписана окружность. Тогда получается из точек \( A,B,C,\) и \( D\) проведено по две касательных, которые равны!
(Вспоминаем о равенстве отрезков касательных проведённых из одной точки)
Итак, у нас
\( \displaystyle BK=BN\) (обозначим \( x\))
\( \displaystyle CK=CL\) (обозначим \( y\))
\( \displaystyle DL=DM\) (обозначим \( z\))
\( \displaystyle AM=AN\) (обозначим \( u\))
И теперь получается, что
\( \begin{array}{*{20}{c}}{AB = x + u}\\{CD = y + z}\end{array} \Rightarrow AB + CD = x + y + z + u\)
и
\( \begin{array}{*{20}{c}}{BC = x + u}\\{AD = u + z}\end{array} \Rightarrow AD + BC = x + y + z + u\)
\( \displaystyle \Rightarrow AB+CD=AD+BC!\)
Обе этих суммы состоят из одинаковых кусочков, просто взятых в разном порядке.
Готово: пункт 1 доказали.
А теперь, наоборот, пункт 2.
Пусть в \( \displaystyle ABCD\) выполняется \( \displaystyle AB+CD=AD+BC\)
Чтобы что-то понять, впишем окружность сперва в такую «кастрюлю» – \( \displaystyle ABCD\) без стороны \( \displaystyle AD\).
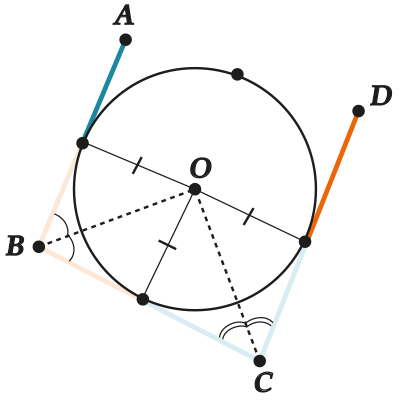
Обрати внимание, что это всегда можно сделать – центром \( \displaystyle O\) такой окружности будет пересечение биссектрис углов \( \displaystyle B\) и \( \displaystyle C\).
Ну вот, в «кастрюле» сидит окружность. При этом сторона \( \displaystyle AD\), если она НЕ касается этой окружности, может либо пересекать её, либо вовсе не иметь с ней общих точек.
Разберём эти случаи и убедимся, что оба они ведут к противоречию.
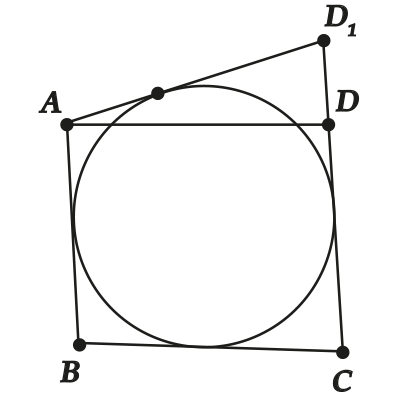
Пусть \( \displaystyle AD\) пересекает окружность. Давай тогда проведём \( \displaystyle A{{D}_{1}}\), которая будет касаться окружности.
По пункту 1 для четырехугольника \( \displaystyle ABC{{D}_{1}}\) должно быть
\( \displaystyle AB+C{{D}_{1}}=A{{D}_{1}}+BC\),
а по условию для четырехугольника \( \displaystyle ABCD\)
\( \displaystyle AB+CD=AD+BC\).
Значит (вычитаем нижнее равенство из верхнего)
\( \displaystyle C{{D}_{1}}-CD=A{{D}_{1}}-AD\)
То есть \( \displaystyle D{{D}_{1}}+AD=A{{D}_{1}}\)
Но так СОВСЕМ не может быть – нарушается неравенство треугольника для \( \Delta AD{{D}_{1}}\):
должно быть \( D{{D}_{1}}+AD>A{{D}_{1}}\), а у нас \( D{{D}_{1}}+AD=A{{D}_{1}}\).
Вот и противоречие. Поэтому точно выяснили, что \( AD\) НЕ МОЖЕТ пересекать окружность.
Пусть теперь \( AD\) «не дотягивается» до окружности:
А теперь посмотрим, как работает эта теорема. Докажем следующее следствие из теоремы.
Если в параллелограмм можно вписать окружность, то это – ромб. Доказательство
Следствие. Если в параллелограмм можно вписать окружность, то это – ромб.
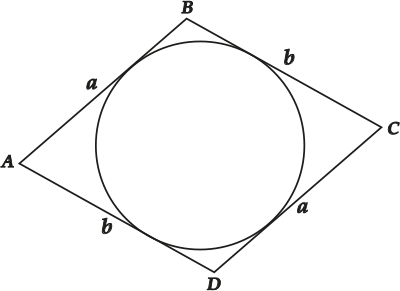
Доказываем: пусть есть параллелограмм \( \displaystyle ABC{{D}}\).
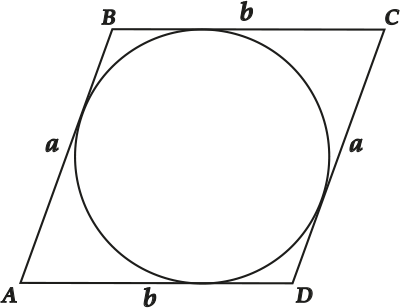
По свойству параллелограмма \( \displaystyle AB=CD~\) (обозначим \( \displaystyle a\)) и \( \displaystyle BC=AD~\) (обозначим \( \displaystyle b\)).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


