Планиметрия — основные понятия и аксиомы
Представь, что ты вдруг очутился на другой планете, ну или… в компьютерной игре.
Перед тобой набор неизвестных продуктов, а твоя задача – приготовить из этого набора как можно больше вкусных блюд. Что тебе понадобится?
Конечно же, правила, инструкции – что можно делать с теми или иными продуктами. А то вдруг ты сваришь то, что едят только в сыром виде или, наоборот, положишь в салат то, что непременно нужно варить или жарить? Так что, без инструкций – никуда!
Хорошо, но к чему такое вступление? При чем тут геометрия? Понимаешь, великое множество утверждений о всяких фигурах в геометрии и есть то самое множество «блюд», которые мы должны научиться готовить.
Но из чего? Из основных объектов геометрии! А вот инструкция по их «употреблению» называется умными словами «система аксиом».
Так что, внимание!
Планиметрия — коротко о главном
Аксиомы принадлежности:
- Аксиома 1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
- Аксиома 2. Через любые две точки можно провести прямую, и только одну.
Аксиомы порядка:
- Аксиома 3. Из трех точек на прямой одна и только одна лежит между двумя другими.
- Аксиома 4. Прямая, лежащая в плоскости, разбивает эту плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Аксиомы мер для отрезков и углов:
- Аксиома 5. Каждый отрезок имеет определенную длину, больше нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
- Аксиома 6. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен \( \displaystyle 180{}^\circ \). Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Аксиомы существования треугольника, равного данному:
- Аксиома 7. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом

Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом
Аксиома параллельных:
- Аксиома 8. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Основные факты об углах:
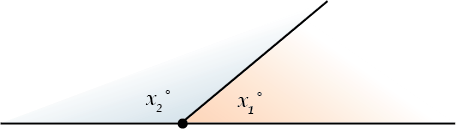
Теорема. Сумма смежных углов равна \( \displaystyle 180{}^\circ \).
\( \displaystyle 180{}^\circ=x_{1}^{{}^\circ }+x_{2}^{{}^\circ }\)
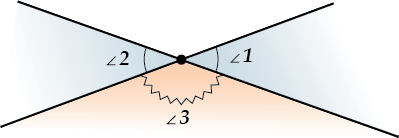
Теорема. Вертикальные углы равны.
\( \displaystyle \angle 1=\angle 2\).
Планиметрия — подробнее

Почему все в картинках и без слов? А нужны ли слова? Мне кажется, на первых порах не очень нужны.
Описания ты найдешь далее в этой статье, а сейчас продолжим картинками.
Что же еще? Ах да, нам же нужно научиться измерять отрезки и углы.
У каждого отрезка есть длина – число, которое этому отрезку (зачем-то …) поставили в соответствие. Длину принято измерять … линейкой, конечно, в сантиметрах, миллиметрах, метрах и даже в километрах.
А теперь измерение углов. Углы почему-то принято измерять в градусах. Почему? На это есть исторические причины, но мы сейчас занимаемся не историей. Поэтому придется принять просто как должное следующее соглашение.

В развернутом угле \( \displaystyle 180\) градусов.
Для краткости пишут: \( \displaystyle {{180}^{\circ }}\). При этом, конечно же, величину всех остальных углов можно найти, если выяснить, какую часть от развернутого угла составляет данный угол.
Инструмент для измерения углов называется транспортир. Думаю, ты его уже не раз в жизни видел.
Два основных факта об углах
I. Смежные углы в сумме составляют \( \displaystyle {{180}^{\circ }}\).
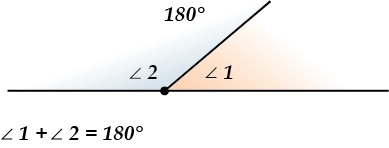
Это совсем естественно, не правда ли? Ведь смежные углы вместе составляют развернутый угол!
II. Вертикальные углы равны.
Почему? А смотри:
\( \displaystyle \angle 1\) и \( \displaystyle \angle 3\) – смежные
\( \displaystyle \Rightarrow \angle 1+\angle 3={{180}^{\circ }}\).\( \displaystyle \angle 2\) и \( \displaystyle \angle 3\) – тоже смежные
\( \displaystyle \Rightarrow \angle 2+\angle 3={{180}^{\circ }}\)

Что теперь?
Ну, конечно, отсюда следует, что \( \displaystyle \angle 1=\angle 2\). (Достаточно, например, вычесть из первого равенства второе. А вообще-то, можно просто посмотреть на картинку).
Прямой угол
Если угол равен смежному с ним, то он называется прямым углом.

Чему равна величина прямого угла?
Ну конечно, \( \displaystyle {{90}^{\circ }}\)! Ведь \( \displaystyle {{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}\).
Острый и тупой углы
Углы, меньшие \( \displaystyle {{90}^{\circ }}\), называются острыми углами.
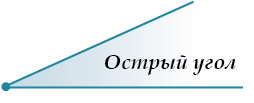
Углы от \( \displaystyle {{90}^{\circ }}\) до \( \displaystyle {{180}^{\circ }}\) называются тупыми углами.

Еще раз: угол в \( \displaystyle {{90}^{\circ }}\)— прямойугол.

Вот, в общем-то и все, что тебе нужно знать для начала. Почему же мы ни слова не сказали об аксиомах?
Аксиомы – это правила действия с основными объектами планиметрии, самые первые утверждения о точках и прямых. Эти утверждения берутся за основу, не доказываются.
Почему же все-таки мы их не формулируем и не обсуждаем? Понимаешь, аксиомы планиметрии в некотором смысле просто описывают ясные интуитивно понятные соотношения довольно длинным математическим языком.
Четкое осознание аксиоматики необходимо чуть позже, когда ты привыкнешь к геометрическим понятиям на уровне здравого смысла.
Тогда – добро пожаловать читай далее эту статью – там довольно подробное обсуждение аксиом.
А пока попробуй поступать как совсем древние греки, до времен Евклида – просто решай задачи, пользуясь здравым смыслом. Уверяю тебя, множество задач тебе поддадутся!
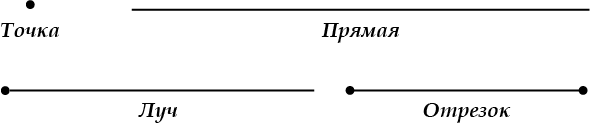
Точка и прямая
Это и есть самые главные понятия планиметрии. Математики говорят, что это «неопределяемые понятия». Как так? А вот так, нужно же с чего-то начинать.
Теперь первые правила обращения с точками и прямыми. Эти правила математики называют «аксиомы» – утверждения, которые принимаются за основу , из которых потом все основное будет выводиться (помнишь, что у нас большая кулинарная миссия по «приготовлению» геометрии?).
Так вот, первая серия аксиом называется «Аксиомы принадлежности».
I. Аксиомы принадлежности
Аксиома 1.1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Обрати внимание, эта аксиома позволяет рисовать так:

и так:

Аксиома 1.2. Через любые две точки можно провести прямую, и только одну.
Вот так: было две точки:

И тут же нашлась прямая:

А другой – нет! Прямая только одна!

Если тебе все это кажется слишком очевидным, то вспомни, что ты – на другой планете и до сих пор совершенно не знал, что делать с объектами «точка» и «прямая».
Луч, отрезок, угол
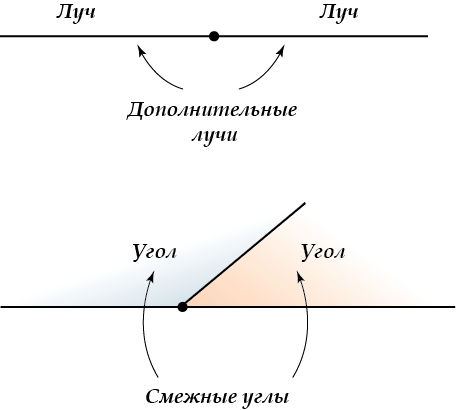
Вот теперь мы научились наносить точки на прямые и проводить прямые через точки, поэтому уже можем приготовить первые простейшие «блюда» — луч, отрезок, угол.
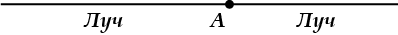
Любая точка, лежащая на прямой, делит эту прямую на две полупрямые. Каждая из этих полупрямых называется еще лучом.
Вот он, луч:


А это отрезок:

Любые две точки на прямой ограничивают отрезок прямой.
Углом называется часть плоскости, заключенная между двумя лучами этой плоскости, имеющими общее начало.
Лучи, образующие угол, называются сторонами угла, а их общее начало– вершиной угла.

Угол, образованный дополнительными лучами, называется развернутым.

Теперь наведем порядок. Следующая серия аксиом так и называется: «Аксиомы порядка».
II. Аксиомы порядка
Аксиома 2.1. Из трех точек на прямой одна и только одна лежит между двумя другими.
Аксиома 2.2. Прямая, лежащая в плоскости, разбивает эту плоскость на две полуплоскости. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.

Теперь – следующий уровень. Нам нужны инструкции по измерению отрезков и углов. Эти аксиомы называются
III. Аксиомы мер для отрезков и углов
Аксиома 3.1. Каждый отрезок имеет определенную длину, больше нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
\( \displaystyle d={{d}_{1}}+{{d}_{2}}\)
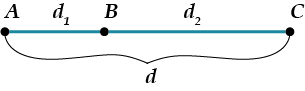
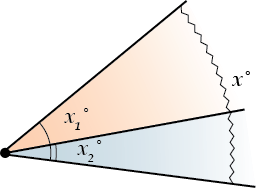
Аксиома 3.2. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен \( \displaystyle 180{}^\circ \). Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
\( \displaystyle x=x_{1}^{{}^\circ }+x_{2}^{{}^\circ }\)
Аксиома 3.3. Каково бы ни было число \( \displaystyle d>0\) , существует отрезок длины \( \displaystyle d\).
А теперь уже совсем странно: «Аксиомы существования треугольника, равного данному».
IV. Аксиомы существования треугольника, равного данному
Аксиома 4.1. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
Более понятными являются два следствия из этой аксиомы:
Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом.

Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом.

Ну, и последняя легендарная аксиома параллельных!
Но сперва определение:
Прямые называются параллельными, если они не имеют общих точек.
V. Аксиома параллельных
Аксиома 5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Ну вот, и закончились аксиомы планиметрии! Слишком много их? Но представь себе, все они нужны. Для каждой из них есть хитрое-хитрое рассуждение, которое показывает, что если удалить эту аксиому, то развалится всё здание геометрии! Ну, или останется нечто, совершенно непохожее на то, к чему мы привыкли.
А теперь два основных факта об углах!
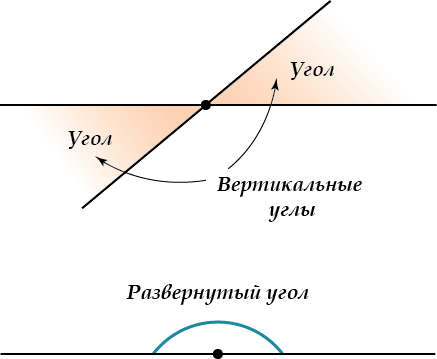
Смежные и вертикальные углы
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами.
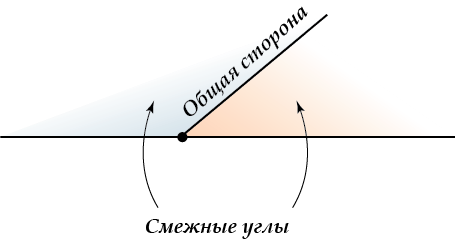
Лучи, образующие угол, называются сторонами угла, а их общее начало – вершиной.
Теорема. Сумма смежных углов равна \( \displaystyle 180{}^\circ \)
\( \displaystyle 180{}^\circ=x_{1}^{{}^\circ }+x_{2}^{{}^\circ }\)

Это совсем простая теорема, правда?
Ведь общая сторона смежных углов просто-напросто разбивает развернутый угол на два угла и поэтому (ВНИМАНИЕ: работает Аксиома 3.2!) сумма смежных углов равна величине развернутого, то есть \( \displaystyle 180{}^\circ \).
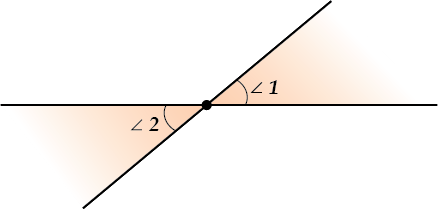
Вертикальные углы проще нарисовать, чем описывать – смотри картинку.
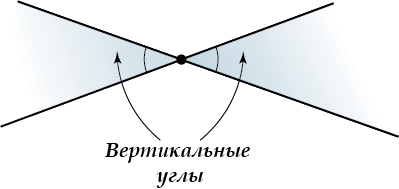
Теорема. Вертикальные углы равны.
Это легкая теорема. Убедись:
\( \displaystyle \angle 1+\angle 3=180{}^\circ \) (они смежные).
\( \displaystyle \angle 2+\angle 3=180{}^\circ \) (тоже смежные)\( \displaystyle \angle 1=\angle 2\) – и ВСЁ!

Прямой, острый и тупой углы
Если угол равен смежному с ним, то он называется прямым.
Его величина равна \( \displaystyle 90{}^\circ \) (ну конечно, ведь \( \displaystyle 90{}^\circ +90{}^\circ =180{}^\circ \))

Углы, меньшие \( \displaystyle 90{}^\circ \), называются острыми углами.


Углы от \( \displaystyle 90{}^\circ \) до \( \displaystyle 180{}^\circ \) называются тупыми углами.
Вот и всё… Дальше нужно говорить о параллельности и о треугольниках. Так что, вперед, в следующие темы.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Анна
08 мая 2018
Большое спасибо!!!
Александр (админ)
08 мая 2018
Пожалуйста, Анна! Удачи на экзаменах.
Виктория
14 мая 2019
Скажите, пожалуйста, есть ли задачник по вашему учебнику геометрии? Может порекомендуете какой-нибудь, чтобы можно было практику проходить (чтоб с ответами)? Теория просто волшебная! Но надо ж закрепить! С уважением
Александр (админ)
14 мая 2019
Конечно есть, Виктория. Задачник, если можно так сказать, находится на сайте 100gia.ru Это тоже наш сайт. Там очень много чего есть, в том числе и задачи по геометрии, с решениями и с ответами. Там вообще более 6000 задач. Изначально все это было на одном сайте. Но потом мы разделили его на два, по просьбам… Спасибо, кстати, за теплые слова. И обязательно закрепляйте. Вы тут абсолютно правы.
Наталья
01 декабря 2019
Ну вот это просто класс! Мой нелюбящий сын геометрию, сегодня после первого вашего урока просто в неё влюбился!
Александр (админ)
01 декабря 2019
Спасибо, огромное, Наталья! Очень приятно слышать. Сыну — успехов в геометрии и удачи на всех экзаменах!