Параллельные прямые
Параллельные прямые – подарок судьбы в решении многих задач.
Они дают тебе множество равных углов! И на них основывается много признаков фигур.
Что, безусловно, будет очень полезно.
Читай эту статью – будешь знать о них все!
И получишь заслуженные баллы на ЕГЭ.
Параллельные прямые — коротко о главном
Определения:
Параллельные прямые – это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: \( \displaystyle a\parallel b\).
Секущая – прямая, пересекающая две параллельные прямые: \( \displaystyle c\).
Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
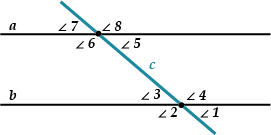
\( \displaystyle \angle 4\) и \( \displaystyle \angle 6\), \( \displaystyle \angle 3\) и \( \displaystyle \angle5\) – внутренние накрест лежащие углы;
\( \displaystyle \angle 5\) и \( \displaystyle \angle 4\), \( \displaystyle \angle 6\) и \( \displaystyle \angle 3\) – внутренние односторонние углы;
\( \displaystyle \angle 1\) и \( \displaystyle \angle 8\), \( \displaystyle \angle 2\) и \( \displaystyle \angle 7\) – внешние односторонние углы;
\( \displaystyle \angle 1\) и \( \displaystyle \angle 5\), \( \displaystyle \angle 4\) и \( \displaystyle \angle 8\), \( \displaystyle \angle 2\) и \( \displaystyle \angle 6\), \( \displaystyle \angle 3\) и \( \displaystyle \angle 7\) – соответственные углы.
Свойства параллельных прямых
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
внутренние накрест лежащие углы равны: \( \displaystyle \angle 3=\angle 5\), \( \displaystyle \angle 4=\angle 6\);
соответственные углы равны: \( \displaystyle \angle 1=\angle 5\), \( \displaystyle \angle 4=\angle 8\), \( \displaystyle \angle 2=\angle 6\), \( \displaystyle \angle 3=\angle 7\);
сумма любых двух внутренних односторонних углов равна \( \displaystyle 180{}^\circ \): \( \displaystyle \angle 3+\angle 6=180{}^\circ \), \( \displaystyle \angle 4+\angle 5=180{}^\circ \);
сумма любых двух внешних односторонних углов равна \( \displaystyle 180{}^\circ \): \( \displaystyle \angle 1+\angle 8=180{}^\circ \), \( \displaystyle \angle 2+\angle 7=180{}^\circ \).
Признаки параллельных прямых

Определение параллельных прямых
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.
Вот, как рельсы

Принято обозначение:
\( \displaystyle a//b\) – читается как \( \displaystyle a\) параллельна \( \displaystyle b\).
Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».
Часто ее еще называют «пятый постулат Евклида». Формулируем:
Аксиома параллельных прямых или пятый постулат Евклида
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
Смотри: через любую точку \( \displaystyle A\) проходит только одна прямая \( \displaystyle b\), которая параллельна \( \displaystyle a\), все остальные будут пересекать прямую \( \displaystyle a\).

Казалось бы: чего проще – ну, одна так одна…
Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых.
В конце концов, уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.
А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.
Ну вот, а теперь возникает два вопроса:
- Если где-то в задаче даны или оказались параллельными две какие-то прямые, то что? Как это использовать?
- А как вообще узнать, что какие-то прямые параллельны?
Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
Термины: секущая, внутренние и внешние углы
Итак, ситуация: две прямые пересечены третьей (она называется секущей)

Получается куча углов. Целых \( \displaystyle 8\) штук.
Приняты такие названия этих углов:
\( \displaystyle \angle 4\) и \( \displaystyle \angle 6\) называются внутренними накрест лежащими углами
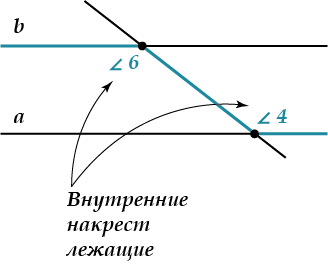
\( \displaystyle \angle 3\) и \( \displaystyle \angle5\) – тоже внутренние накрест лежащие углы.
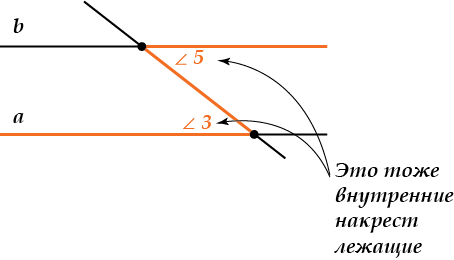
Название говорит само за себя: \( \displaystyle \angle 4\) и \( \displaystyle \angle 6\), так же, как и \( \displaystyle \angle 3\) и \( \displaystyle \angle5\) лежат «накрест» — по разные стороны от секущей и «внутри», между прямыми \( \displaystyle a\) и \( \displaystyle b\).
\( \displaystyle \angle 5\) и \( \displaystyle \angle 4\) (а еще \( \displaystyle \angle 6\) и \( \displaystyle \angle 3\)) называются внутренними односторонними углами.
Они лежат с одной стороны от секущей и «внутри» между прямыми \( \displaystyle a\) и \( \displaystyle b\).
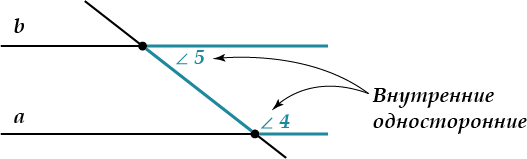
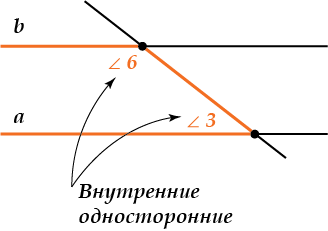
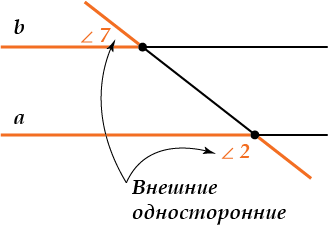
\( \displaystyle \angle 1\) и \( \displaystyle \angle 8\) (а еще \( \displaystyle \angle 2\) и \( \displaystyle \angle 7\)) называются внешними односторонними углами (ты уже догадался, почему?)
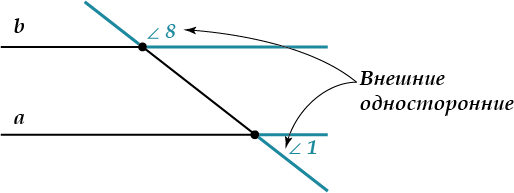
И последнее название: соответственные углы.
Это пары углов:
- \( \displaystyle \angle 1\) и \( \displaystyle \angle 5\)
- \( \displaystyle \angle 4\) и \( \displaystyle \angle 8\)
- \( \displaystyle \angle 2\) и \( \displaystyle \angle 6\)
- \( \displaystyle \angle 3\) и \( \displaystyle \angle 7\)
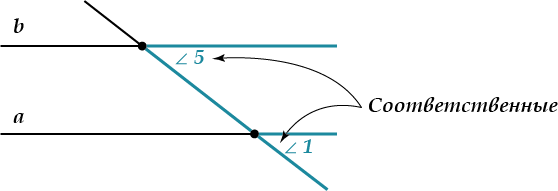
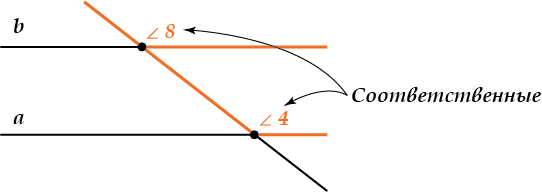
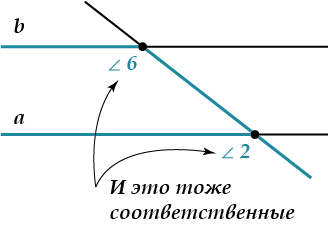
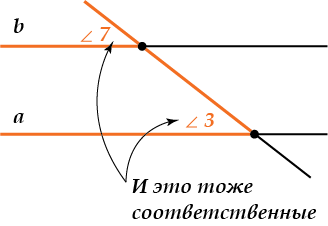
Обрати внимание, \( \displaystyle \angle 1\) и \( \displaystyle \angle 5\) лежат в одинаковых «соответственных» местах около точек \( \displaystyle A\) и \( \displaystyle B\). То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.
Свойства параллельных прямых
Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если \( \displaystyle a//b\), то что?
И вот что:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- Внутренние накрест лежащие углы равны
- Соответственные углы равны
- Сумма любых двух внутренних односторонних равна \( \displaystyle 180{}^\circ \)
Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.
А теперь, наоборот, признаки параллельных прямых.
Признаки параллельных прямых
То есть, как бы узнать, что прямые параллельны?
Если две прямые (\( \displaystyle a\) и \( \displaystyle b\)) пересечены третьей и оказалось, что:
- Какие-нибудь два накрест лежащих угла равны, ИЛИ
- Какие нибудь два соответственных угла равны, ИЛИ
- Сумма хоть каких-то двух внутренних односторонних равна \( \displaystyle 180{}^\circ \), ИЛИ
- Сумма хоть каких – то двух внешних односторонних равна \( \displaystyle 180{}^\circ \),
то прямые \( \displaystyle a\) и \( \displaystyle b\) – параллельны
Заметь, что для того, чтобы установить параллельность прямых, достаточно выяснить, скажем, равенство всего двух углов (или накрест лежащих, или соответственных), а уже все остальное окажется , так сказать, бонусом.
Смотри-ка, вот схема:

Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Григорий
09 мая 2018
спасибо за подробную информацию!
Александр (админ)
09 мая 2018
Пожалуйста, Григорий! Приходи еще и делись инфой с друзьями!
Александр
27 июня 2018
Спасибо , очень помогает.
Александр (админ)
27 июня 2018
Пожалуйста, Александр. Мы рады!))
Елена
03 июля 2018
Класс!!!!!! Всё просто, понятно и наглядно. Легко усвоилось. Спасибо. Очень нужная информация.
Александр (админ)
03 июля 2018
Отлично, Елена, что так помог наш текст. Делись им с друзьями, окажешь услугу и им и нам! И удачи на экзамене.
Алексей
17 сентября 2018
очень понятно! Спасибо-о-о-о-о-о-о-о
Александр (админ)
17 сентября 2018
Очень рады, Алексей! Спасибо и тебе.
Никита
25 декабря 2018
Спасибо огромное. Кстати мне помогло в школе
Александр (админ)
25 декабря 2018
Пожалуйста, Никита! Нам очень приятно.
Виктор
09 февраля 2020
Весь материал полезен , но практически все можно найти в школьном учебнике. А вот это замечание : «…но эти геометрии уже оказываются не геометриями на плоскости, а геметриями на каких-то хитрых поверхностях.» — очень уместно. Сколько приходилось знакомиться с геометрией Лобачевского, везде авторы избегают этого разъяснения, а ведь оно сразу снимает все вопросы, возникающие у дилетанта.
Александр (админ)
09 февраля 2020
Спасибо, Виктор.