Параллелограмм — признаки и свойства
Привет!
Клод Бернард однажды сказал:
«Думать, что всё знаешь, останавливает тебя от того, чтобы учиться новому»
Давай узнаем что-то новое сегодня, разбирая, казалось бы, такую простую тему!
Статья поможет тебе окончательно разобраться с самыми «популярными» параллелограммами, а наши вебинары дадут тебе необходимую практику.
И на ЕГЭ ты сможешь решить любую задачу на эту тему!
Параллелограмм — коротко о главном
Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.
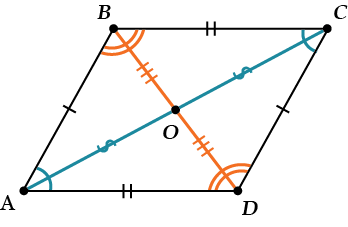
Свойства параллелограмма:
- Противоположные стороны равны: \( \displaystyle AB=CD\), \( \displaystyle AD=BC\).
- Противоположные углы равны: \( \displaystyle \angle A=\angle C\), \( \displaystyle \angle B=\angle D\).
- Углы при одной стороне составляют в сумме \( \displaystyle 180{}^\circ \): \( \displaystyle \angle A+\angle B=180{}^\circ \), \( \displaystyle \angle B+\angle C=180{}^\circ \), \( \displaystyle \angle C+\angle D=180{}^\circ \), \( \displaystyle \angle A+\angle D=180{}^\circ \).
- Диагонали делятся точкой пересечения пополам: \( \displaystyle BO=OD; AO=OC\).
Прямоугольник – четырехугольник, все углы которого прямые: \( \displaystyle \angle A=\angle B=\angle C=\angle D=90{}^\circ \).
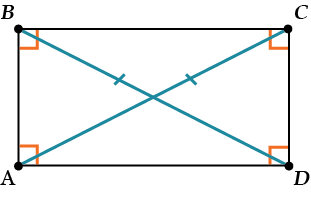
Свойства прямоугольника:
- Диагонали прямоугольника равны: \( \displaystyle AC=BD\).
- Прямоугольник – параллелограмм (для прямоугольника выполняются все свойства параллелограмма).
Ромб – четырехугольник, все стороны которого равны между собой: \( \displaystyle AB=BC=CD=DA\).
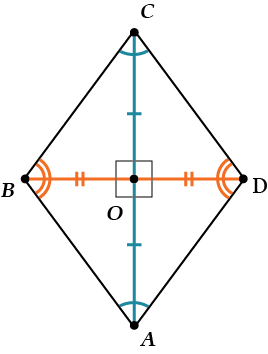
Свойства ромба:
- Диагонали ромба перпендикулярны: \( \displaystyle AC\bot BD\).
- Диагонали ромба являются биссектрисами его углов: \( \displaystyle \angle BAC=\angle CAD\); \( \displaystyle \angle BCA=\angle DCA\); \( \displaystyle \angle CBD=\angle DBA\); \( \displaystyle \angle CDB=\angle BDA\).
- Ромб – параллелограмм (для ромба выполняются все свойства параллелограмма).
Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые: \( \displaystyle AB=BC=CD=DA\); \( \displaystyle \angle A=\angle B=\angle C=\angle D=90{}^\circ \).
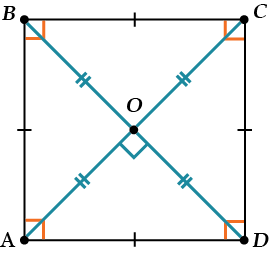
Свойства квадрата:
- Квадрат – ромб и прямоугольник одновременно, следовательно для квадрата выполняются все свойства прямоугольника и ромба. А также:
\( \displaystyle ABCD\) – ромб
Параллелограмм — определения и свойства
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Параллелограмм –это четырехугольник, противоположные стороны которого попарно параллельны
Смотри:

Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:
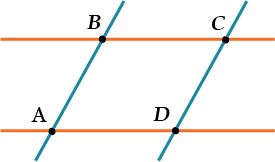
И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться для ее решения.
Итак,
В любом параллелограмме:
1. Противоположные стороны равны: \( \displaystyle AB=CD\) и \( \displaystyle AD=BC\).
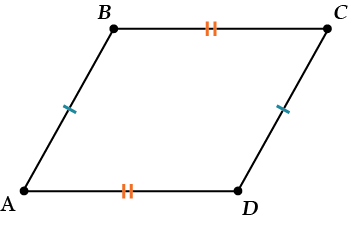
2. Противоположные углы равны: \( \displaystyle \angle A=\angle C\) и \( \displaystyle \angle B=\angle D\).

3. Диагонали делятся пополам точкой пересечения. \( \displaystyle AO=OC\) и \( \displaystyle BO=OD\).
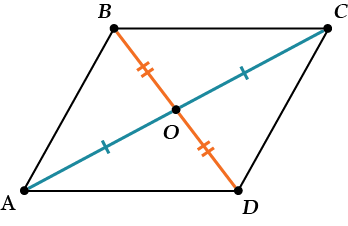
Видишь, какое богатство выбора? Что же использовать в задаче?
Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Доказательство свойств параллелограмма
Давай проведём диагональ ????????. Что получится?
Два треугольника: ???????????? и ????????????.
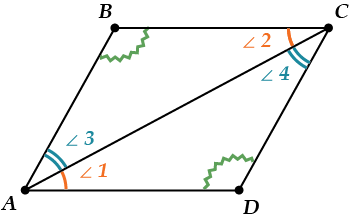
Раз ???????????????? – параллелограмм, то:
- \( \displaystyle AD||BC\) \( \displaystyle \Rightarrow ~\angle 1=\angle 2\) как накрест лежащие;
- \( \displaystyle AB||CD\ \) \( \displaystyle \Rightarrow ~\angle 3=\angle 4\) как накрест лежащие.
Значит, \( \displaystyle \Delta ABC=\Delta ADC\) (по II признаку: \( \displaystyle \angle 1=\angle 2,~~\angle 3=\angle 4~\) и \( \displaystyle AC\) — общая.)
Ну вот, а раз \( \displaystyle \Delta ABC=\Delta ADC\), то \( \displaystyle AB=CD\) и \( \displaystyle AD=BC\) – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2) и осталось только 3)!
Почему?
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма
Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм.
В значках это так:
\( \displaystyle AB=CD\);\( \displaystyle AB\parallel CD\) \( \displaystyle \Rightarrow \) \( \displaystyle ABCD\) – параллелограмм.
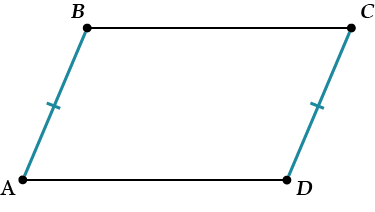
Почему? Хорошо бы понять, почему \( \displaystyle AD\parallel BC\) – этого хватит. Но смотри:
Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
\( \displaystyle AB=CD\), \( \displaystyle AD=BC\) \( \displaystyle \Rightarrow\) \( \displaystyle ABCD\) – параллелограмм.
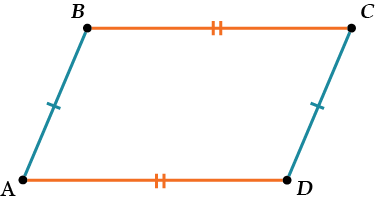
Ну, это ещё легче!
Снова проведём диагональ \( \displaystyle AC\).
Теперь \( \displaystyle \Delta ABC=\Delta ACD\) просто по трём сторонам.
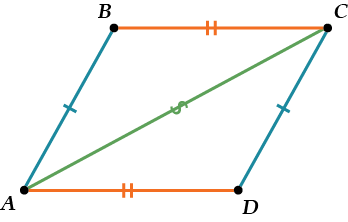
А значит:
Признак 3. Если у четырёхугольника противоположные углы равны, то это – параллелограмм.
\( \displaystyle \angle A=\angle C\), \( \displaystyle \angle B=\angle D\) \( \displaystyle \Rightarrow \) \( \displaystyle ABCD\) – параллелограмм.

И тоже несложно. Но… по-другому!
Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
\( \displaystyle AO=OC\); \( \displaystyle BO=OD\) \( \displaystyle \Rightarrow \) \( \displaystyle ABCD\) – параллелограмм.
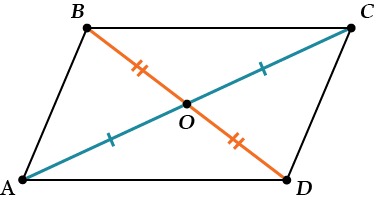
И опять просто:
Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

Прямоугольник — определение и свойства
Думаю, что для тебя вовсе не явится новостью то, что…
Прямоугольник – четырехугольник, все углы которого прямые.

Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является!
Ведь у него \( \displaystyle \angle A=\angle C\left( =90{}^\circ \right)\) и \( \displaystyle \angle B=\angle D\left( =90{}^\circ \right)\) — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма \( \displaystyle AB=CD\) и \( \displaystyle BC=AD\), а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительное свойство.
Диагонали прямоугольника равны: \( \displaystyle AC=BD\).

Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
Если у параллелограмма равны диагонали, то это – прямоугольник.

Обрати внимание! Речь идёт о параллелограммах! Не любой четырехугольник с равными диагоналями – прямоугольник, а только параллелограмм!
Докажем, что диагонали прямоугольника равны
Пункт о параллелограмме совсем очевидный – ведь просто выполнен признак 3 (\( \displaystyle \angle A=\angle C\) \( \displaystyle \angle B=\angle D\))
А пункт о диагоналях – очень важный. Итак, докажем, что диагонали прямоугольника равны.
Ромб — определение и свойства
Ромб – четырехугольник, все стороны которого равны между собой.
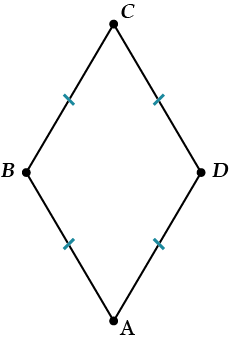
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него \( \displaystyle AB=CD\) и \( \displaystyle BC=AD\) (Вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
Свойство 1. Диагонали ромба перпендикулярны.
Почему? Ну, раз ромб – это параллелограмм, то его диагонали делятся пополам.
Поэтому \( \displaystyle \Delta BOC=\Delta DOC\) по трём сторонам (\( \displaystyle BO=OD\), \( \displaystyle OC\) — общая, \( \displaystyle BC=CD\)).
И значит, \( \displaystyle \angle BOC=\angle COD\), но они смежные!
\( \displaystyle \Rightarrow \angle BOC=90{}^\circ \) и \( \displaystyle \angle COD=90{}^\circ \).
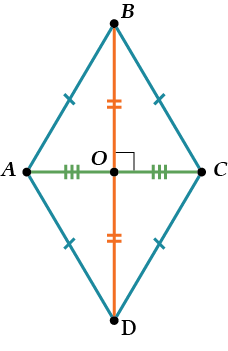
Свойство 2. Диагонали ромба являются биссектрисами его углов.
Почему? Да потому же!
Из-за того, что диагонали делятся точкой пересечения пополам, а все стороны ромба равны, весь ромб оказался разделён диагоналями на четыре равных треугольника:
\( \displaystyle \Delta BOC,\text{ }\Delta BOA,\ \Delta AOD,\text{ }\Delta COD\).
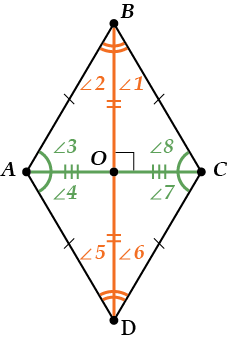
Поэтому
\( \displaystyle \angle 1=\angle 2;\text{ }\angle 5=\angle 6;\) \( \displaystyle \angle 3=\angle 4;\text{ }\angle 7=\angle 8;\)Иными словами, диагонали \( \displaystyle BD\) и \( \displaystyle AC\) оказались биссектрисами углов ромба.
Как в случае с прямоугольником, свойства эти – отличительные, каждые из них является ещё и признаком ромба.
Признаки ромба
Признак 1. Если в параллелограмме диагонали перпендикулярны то это – ромб.
\( \displaystyle \left\{ \begin{array}{l}AC\bot BD\\ABCD\ — параллелограмм\end{array} \right.\Rightarrow\)
\( \displaystyle \Rightarrow \) \( \displaystyle ABCD\) – ромб
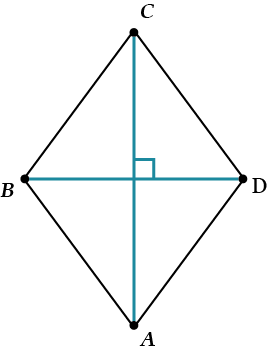
Почему? Смотри:
\( \displaystyle ABCD\) – параллелограмм \( \displaystyle \Rightarrow AO=CO;BO=OD\).
Но ещё дано, что \( \displaystyle AC\bot BD\) \( \displaystyle \Rightarrow\) \( \displaystyle \Delta AOB=\Delta BOC=\Delta COD=\Delta AOD\) – по двум катетам.
И значит, \( \displaystyle AB=BC=CD=AD\) – и всё!
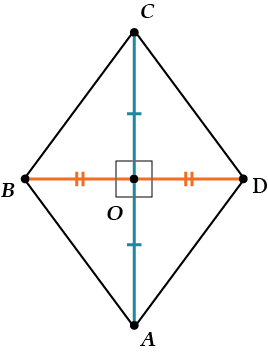
Признак 2. Если в параллелограмме хотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.
А это почему? А посмотри:
\( \displaystyle \angle A=\angle C\), так как \( \displaystyle ABCD\) – параллелограмм.
Но ещё дано, что \( \displaystyle AC\) – биссектриса углов \( \displaystyle A\) и \( \displaystyle C\).

Значит, \( \displaystyle \Delta ABC=\Delta ADC\) и оба этих треугольника – равнобедренные.
Значит, \( \displaystyle AB=BC=CD=DA\), то есть \( \displaystyle ABCD\) – ромб.
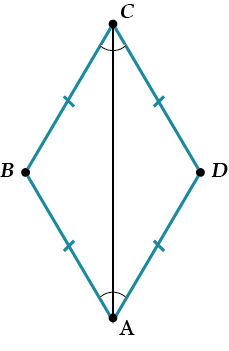
И снова обрати внимание! Не всякий четырёхугольник с перпендикулярными диагоналями – ромб.
Вот пример. Разве это ромб?
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ \( \displaystyle AC\) – биссектриса углов \( \displaystyle A\) и \( \displaystyle C\).
Но … диагонали не делятся, точкой пересечения пополам, поэтому \( \displaystyle ABCD\) – НЕ параллелограмм, а значит, и НЕ ромб.

Чтобы быть ромбом, четырёхугольник сперва должен «стать» параллелограммом, а потом уже демонстрировать признак 1 или признак 2.
Квадрат — определения и свойства
Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые.
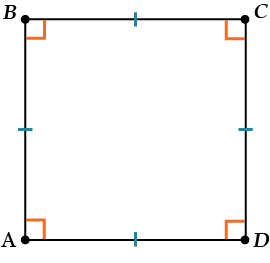
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
У квадрата угол между диагональю и стороной равен \( \displaystyle 45{}^\circ \).
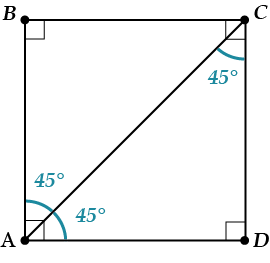
Понятно, почему?
Квадрат – ромб \( \displaystyle \Rightarrow \) \( \displaystyle AC\) – биссектриса угла \( \displaystyle A\), который равен \( \displaystyle 90{}^\circ \).
Значит \( \displaystyle AC\) делит \( \displaystyle \angle A\) (да и \( \displaystyle \angle C\) тоже) на два угла по \( \displaystyle 45{}^\circ \).
Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам.
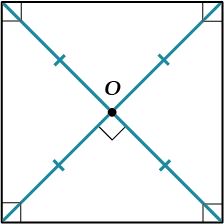
Ну, это совсем ясно: прямоугольник \( \displaystyle \Rightarrow \) диагонали равны; ромб \( \displaystyle \Rightarrow \) диагонали перпендикулярны, и вообще – параллелограмм \( \displaystyle \Rightarrow \) диагонали делятся точкой пересечения пополам.
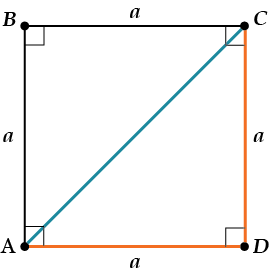
Если сторона квадрата равна \( \displaystyle a\), то его диагональ равна \( \displaystyle a\sqrt{2}\).
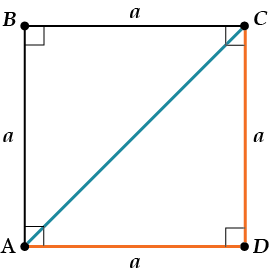
Почему? Ну, просто применим теорему Пифагора к \( \displaystyle \Delta ADC\).
\( \displaystyle A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}\)Значит, \( \displaystyle AC=\sqrt{2}\cdot a\)
На этом с теорией, связанной с параллелограммом мы закончим. Если вы хотите попрактиковаться в решении задач, смотрите наши вебинары из бонусной части.
Бонус 1: Площадь фигур на клечатой бумаге — вебинар из нашего курса подготовки к ЕГЭ по математике
Хотя начиная с 2021 году задача на геометрию на клечатой бумаге не будет входить в ЕГЭ, она очень полезна для того, чтобы начать изучать геометрию, для понимания планиметрии.
На этом вебинаре мы научимся находить длины отрезков; вспомним формулы площади треугольника, параллелограмма и трапеции.
И не только вспомним, но и научимся применять в задаче №3 из ЕГЭ.
А также мы узнаем ещё два универсальных способа нахождения площадей любых многоугольников — с помощью прямоугольной рамки и с помощью разрезания.
Бонус 2. Параллелепипед. Куб. Призма – вебинар из нашего курса подготовки к ЕГЭ по математике
Итак, куб, параллелепипед и призма — задача №8 из ЕГЭ.
На этом вебинаре мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
И закрепим все на большом количестве задач.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



????????????????????????
Спасибо! )))
Некоторые комментарии прошлых лет к этой статье:
максим
26 марта 2019
молодцы
Даниил
03 июня 2019
Спасибо очень помогли!
Алёшка
25 мая 2020
Молодцы просто, имеете могёти просто, чётко