Площади фигур (плоских и объемных)
Сначала мы рассмотрим площади плоских фигур.
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
- Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)
В примере на рисунке:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
- Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
- Подставить найденные значения в уравнение площади.
Пусть нужно найти площадь трапеции, построенной на листе в клетку.
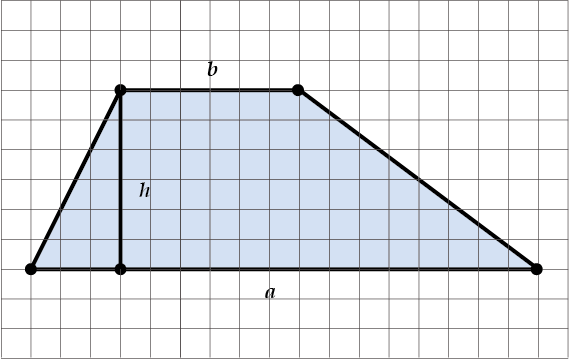
Просто считаем клеточки и видим, что в нашем случае \( \displaystyle a=17\), \( \displaystyle b=6\) и \( \displaystyle h=6\). Подставляем в формулу:
\( \displaystyle S=\frac{a+b}{2}\cdot h=\frac{17+6}{2}\cdot 6=69\)Но бывает, что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:
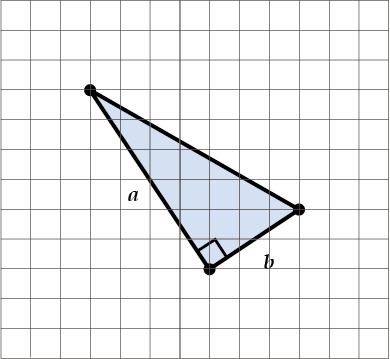
Вроде бы даже прямоугольный и \( \displaystyle S=\frac{1}{2}\cdot ab\), но чему тут равно \( \displaystyle a\), и чему равно \( \displaystyle b\)?
Как узнать?
Найдем \( \displaystyle a\) по теореме Пифагора из \( \displaystyle \Delta ADC\), а \( \displaystyle b\) по теореме Пифагора из \( \displaystyle \Delta BCE\).
Благо на листе в клетку легко посчитать длину катетов.
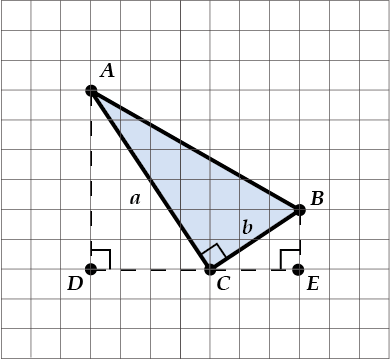
Итак:
\( \displaystyle {{a}^{2}}=A{{D}^{2}}+D{{C}^{2}}={{6}^{2}}+{{4}^{2}}=52\)
Значит, \( \displaystyle a=\sqrt{52}=2\sqrt{13}\)
Теперь \( \displaystyle {{b}^{2}}=B{{E}^{2}}+C{{E}^{2}}={{2}^{2}}+{{3}^{2}}=13\).
\( \displaystyle b=\sqrt{13}\)
Подставляем в формулу:
\( \displaystyle S=\frac{1}{2}\cdot ab=\frac{1}{2}\cdot 2\sqrt{13}\cdot \sqrt{13}=13\).
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
- Достроить искомую фигуру до прямоугольника;
- Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
- Из площади прямоугольника вычесть сумму площадей всех лишних фигур.
Давай посчитаем площадь того же треугольника вторым способом.

Нужно окружить нашу фигуру прямоугольником. Вот так:
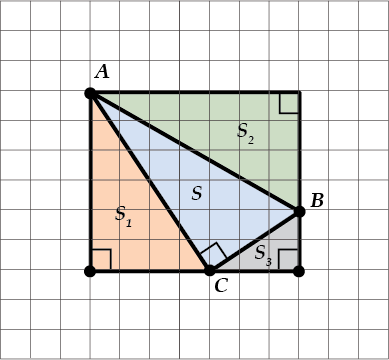
Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!
Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 7=42\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot 7\cdot 4=14\)
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 3\cdot 2=3\)
\( \displaystyle \Rightarrow S=42-12-14-3=13\)
Почему бы просто не считать клеточки?
Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.
Вот, например, трапеция:
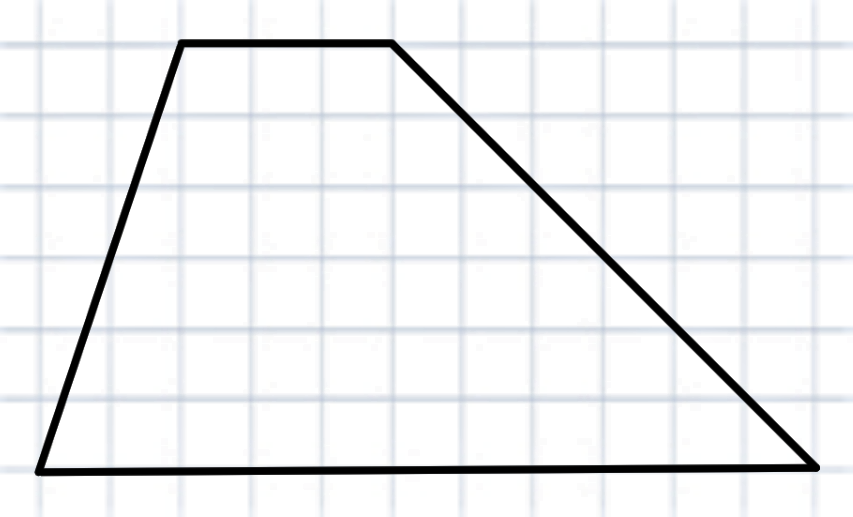
Посчитаем клеточки: их всего 46, верно?
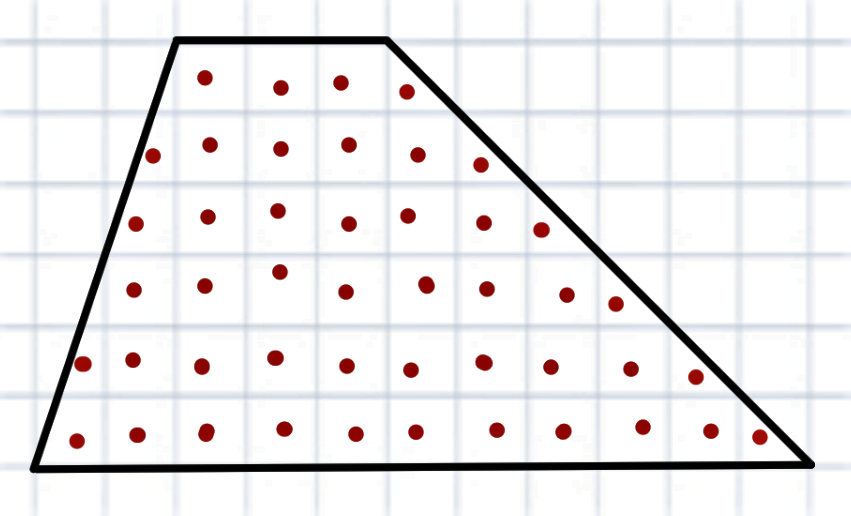
Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе \( 36+\frac{10}{2} = 41\)
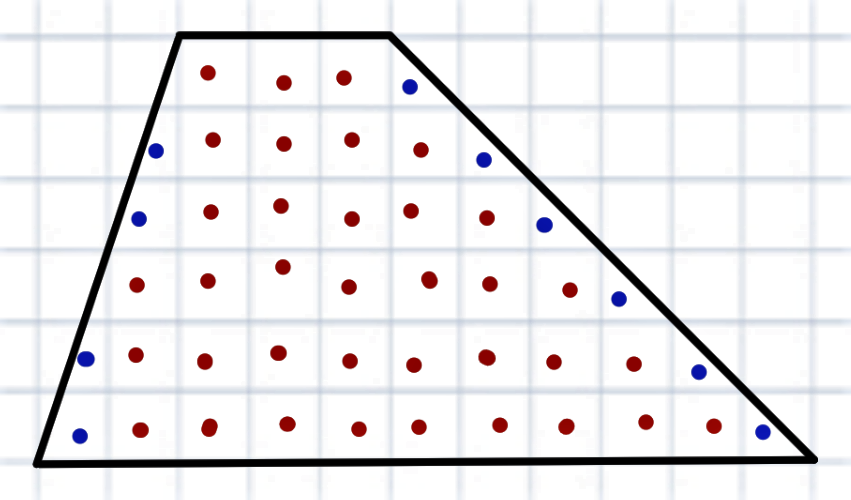
Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…
Как всё это учитывать?
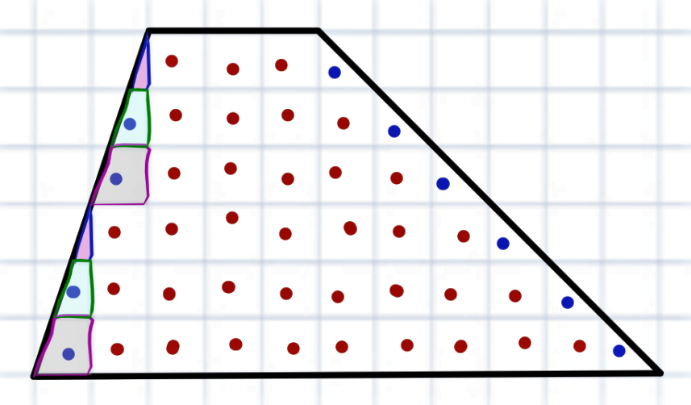
Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.
А жёлтые сколько занимают? Постарайтесь ответить сами.
Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.
Итак, 2 жёлтых куска = 1 клетка.
Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.
Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это \( 36+\frac{6}{2}=39\) клетки.
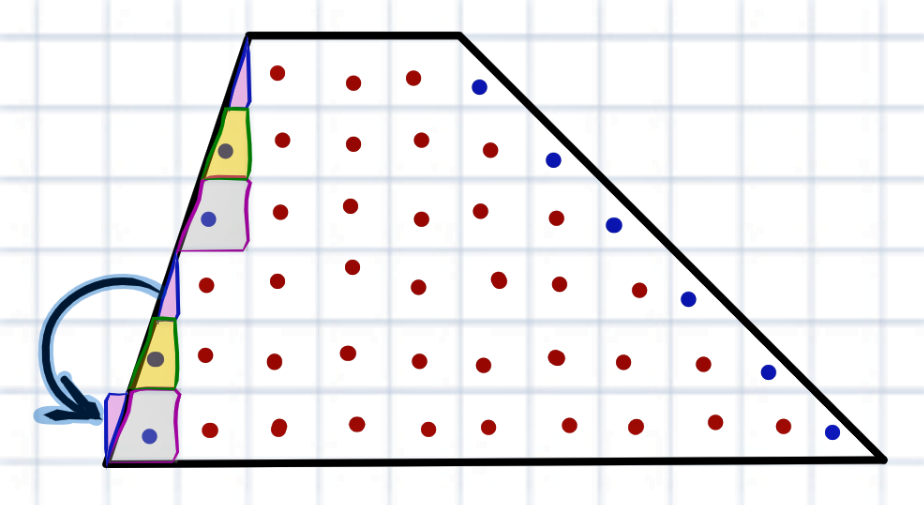
Итого клеток: \( 1 + 2 + 39 = 42\).
Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.
Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).
Способ 3. Формула Пика
Существует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.
Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
Сколько насчитали?
У меня получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Ну а теперь сама формула:
Делим границу пополам, прибавляем внутренности и вычитаем 1:
\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)
Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂
Как запомнить формулу Пика
Всё, что внутри, берём целиком (клетки внутри фигуры целые).
Граница режет клетки надвое, поэтому берём половину узлов границы.
Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? \( Г = 4.\) А сколько внутри? \( В = 0\) (нисколько)
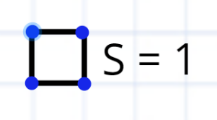
Границу делим пополам, получаем 2. Прибавляем внутренности (+0) – ничего не поменялось.
Очевидно, что осталось вычесть 1, чтобы получить 1.
Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.
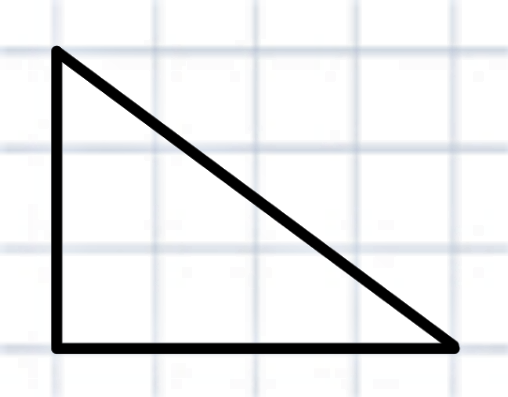
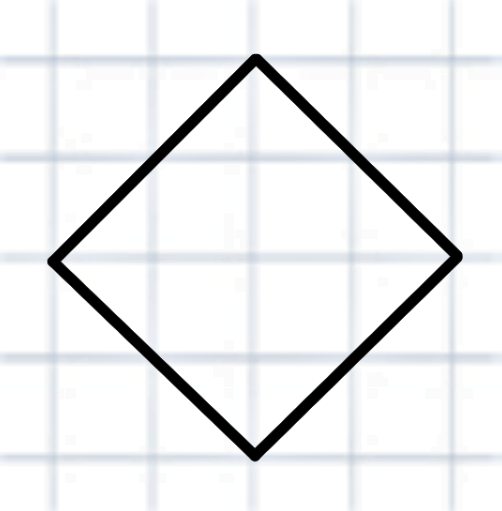
Вычислите площадь простых фигур тремя способами
Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.


Вычислите площадь произвольных фигур по формуле Пика
Вычислите самостоятельно площади фигур с помощью формулы Пика:
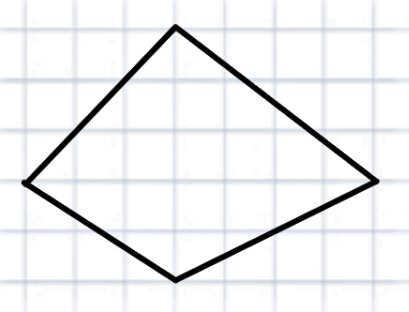
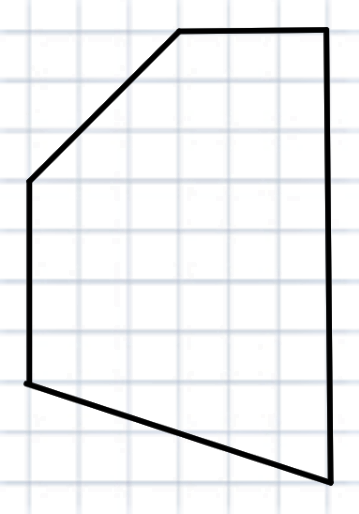
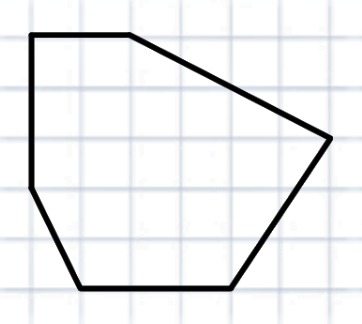
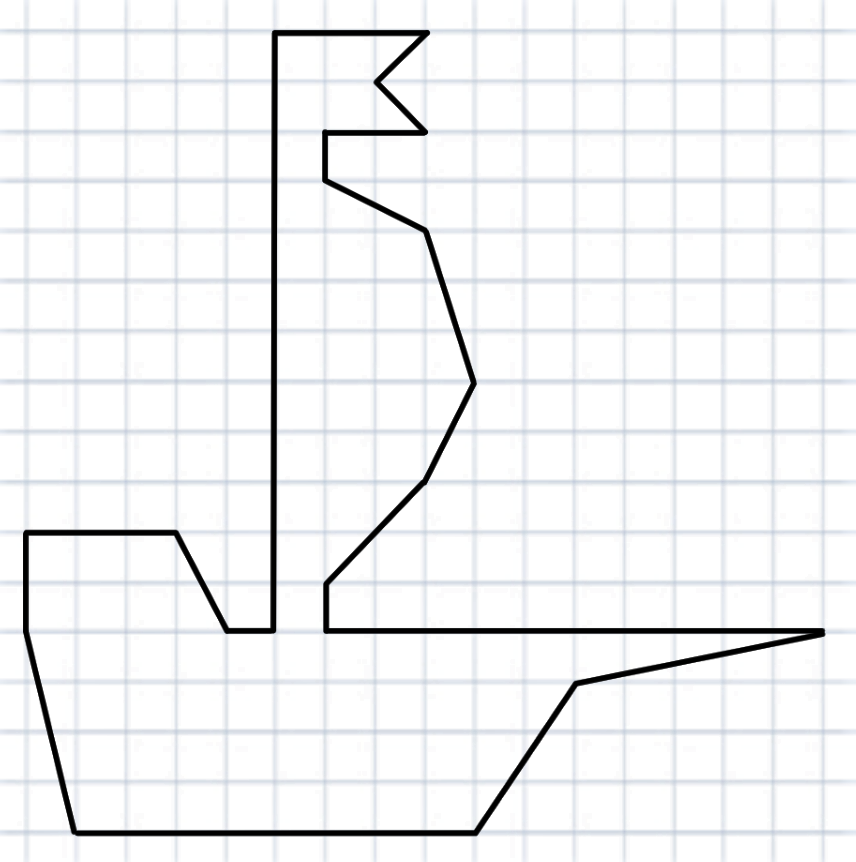
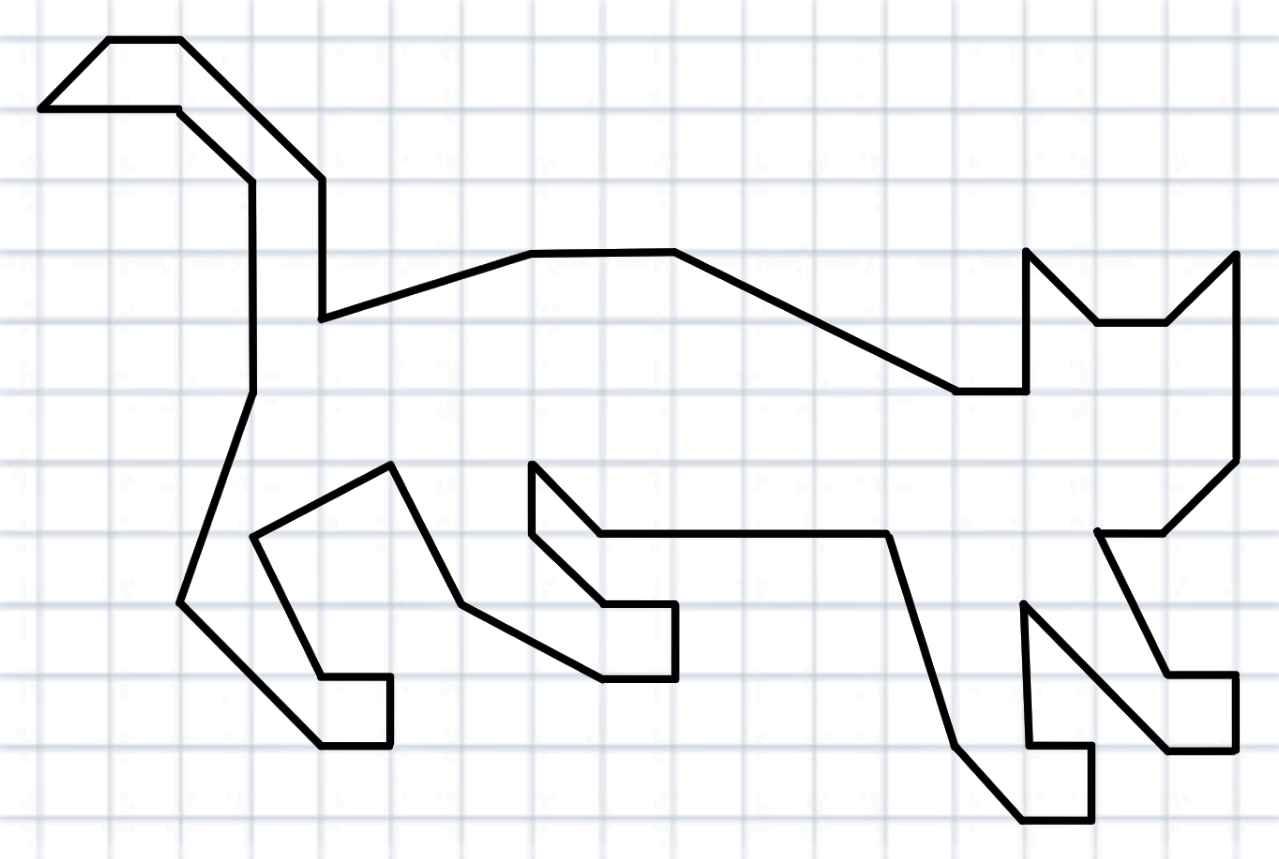
Посчитайте площадь корабля и котика по формуле Пика
Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!
Фигуры с отверстиями — посчитайте площади двумя способами
Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?
Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?
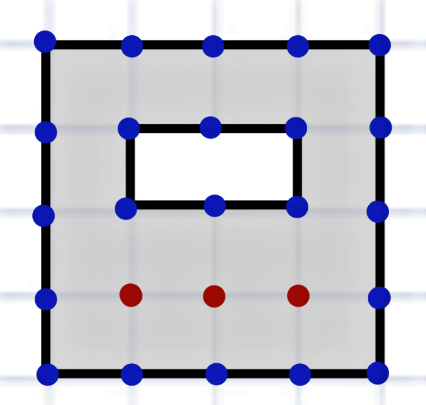
Проверим на простом примере: это квадрат \( 4\times 4\), и в нём вырезан прямоугольник \( 1\times 2\), значит, его площадь \( 16-2=14\).
А теперь по точкам. На границах (включая внутренние) \( Г = 22\). Внутри \( В = 3\). Тогда площадь по формуле Пика
\( S = \frac{22}{2} + 3 -1 = 13.\)
Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.
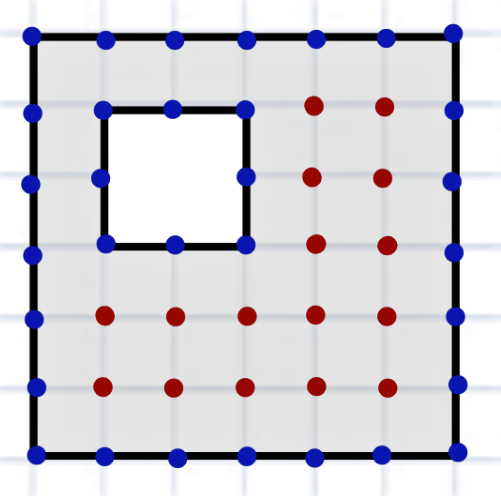
Сосчитай сам и проверь.
Что получилось?
У меня снова на 1 меньше.
Так может быть просто формулу немного «подкрутить»? Нет!
Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.
Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.
Когда формулу Пика применять нельзя?
Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.
Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.
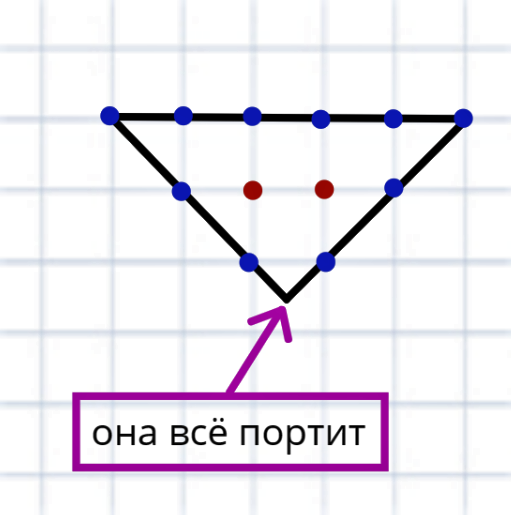
Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть
\( Г = 10, В = 2, S = \frac{10}{2} + 2 – 1 = 6.\)
А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.
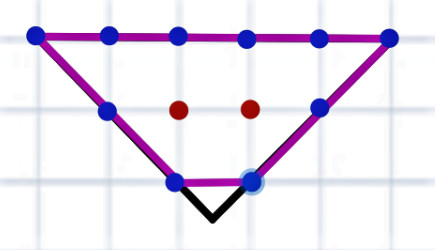
Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.
Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Какой способ лучше?
Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.
Вот смотри, нужно посчитать площадь такой фигуры:
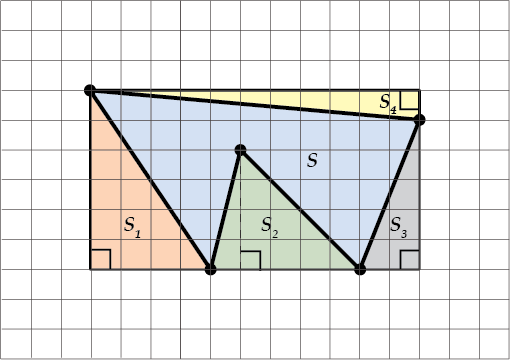
Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.
А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).
\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)
\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)
\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).
\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)
\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).
Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).
\( \displaystyle S=66-12-10-5-5,5=33,5\)
Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?
Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.
С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.
Поэтому использование того или иного способа зависит лишь от конкретной задачи.
ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР
Площадь поверхности призмы
Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
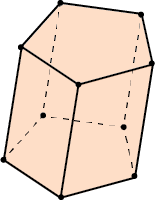
Площадь полной поверхности призмы – это сумма площадей всех граней.
\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+2\cdot {{S}_{основания\ \ }}\)
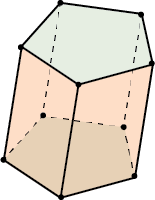
Формулу можно написать для прямой призмы:
\( \displaystyle {{\text{S}}_{боков.}}=\text{H}\cdot \text{P}\), где \( \displaystyle P\) — периметр основания.
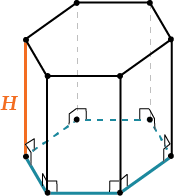
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы. Для примера посчитаем полную поверхность правильной шестиугольной призмы.
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
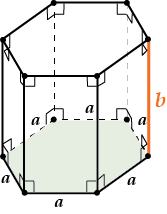
Все боковые грани – прямоугольники. Значит \( \displaystyle {{\text{S}}_{\text{бок.}}}=6\cdot \text{ab}\).
\( \displaystyle {{\text{S}}_{осн.}}=\frac{3\sqrt{3}}{2}{{\text{a}}^{2}}\) — это уже выводили при подсчёте объёма.
Итак, получаем:
\( \displaystyle {{\text{S}}_{\text{полн.}}}=6\text{ab}+3\sqrt{3}{{\text{a}}^{2}}\).
Площадь поверхности пирамиды
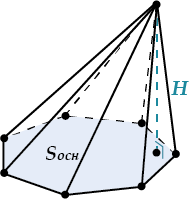
Для пирамиды тоже действует общее правило:
Площадь полной поверхности пирамиды – это сумма площадей всех граней.\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+{{S}_{основания\ \ }}\)
Теперь давай посчитаем площадь поверхности самых популярных пирамид.
Площадь поверхности правильной треугольной пирамиды
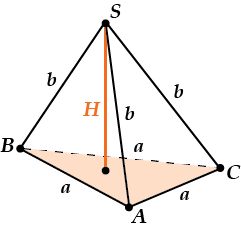
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle {{S}_{ASB}}\).
И тогда
\( \displaystyle {{S}_{полн. пов.\ \ }}=3{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)
Вспомним теперь, что
\( \displaystyle {{S}_{осн}}\) — это площадь правильного треугольника \( \displaystyle ABC\).
И еще вспомним, как искать эту площадь.
Используем формулу площади:
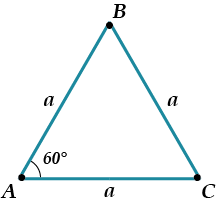
\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \).
У нас «\( \displaystyle a\)» — это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60{}^\circ =\frac{\sqrt{3}}{2}\).
Значит, \( \displaystyle {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\frac{\sqrt{3}}{2}=\frac{{{a}^{2}}\sqrt{3}}{4}\).
Теперь найдем \( \displaystyle {{S}_{\Delta ASB}}\).
Пользуясь основной формулой площади и теоремой Пифагора, находим
\( \displaystyle {{S}_{\Delta ASB}} = \frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)
Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:
\( \displaystyle S={{a}^{2}}\sqrt{3}\).
Площадь поверхности правильной четырехугольной пирамиды
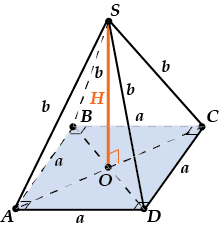
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
\( \displaystyle {{S}_{полн. пов.\ \ }}=4{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)
В основании – квадрат, и поэтому \( \displaystyle {{S}_{OCH}}={{a}^{2}}\).
Осталось найти площадь боковой грани
\( \displaystyle {{S}_{\Delta ASB}} = \frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)Площадь поверхности правильной шестиугольной пирамиды
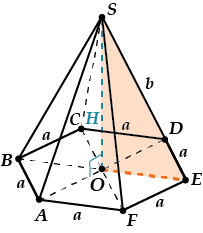
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).
\( \displaystyle {{S}_{полн. пов.\ \ }}=4{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)
Как найти \( \displaystyle {{S}_{OCH}}\)?
Шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете площади поверхности правильной треугольной пирамиды, здесь используем найденную формулу.
\( \displaystyle {{S}_{ABCDEF}}=6\cdot {{S}_{AOF}}=6\cdot \frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3\sqrt{3}{{a}^{2}}}{2}\)
Ну, и площадь боковой грани мы уже искали аж два раза
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.
И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!
Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!
ЕГЭ №3. Площадь фигур на клетчатой бумаге
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


