Площади треугольника и других плоских фигур
Что такое площадь?
Странный вопрос – не правда ли?
В обычной жизни мы привыкли к тому, что у всяких плоских фигур (таких как поверхность стола, стула, пол наших квартир и т.д.) есть не только длина и ширина, но и какая-то еще характеристика, которую мы, не задумываясь, называем площадью.
А теперь вот давай задумаемся: что же все-таки такое площадь?
Площади треугольника — коротко о главном
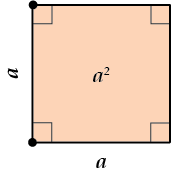
Квадрат
\( \displaystyle \Large S={{a}^{2}}\)
Прямоугольник
\( \displaystyle \Large S=ab\)

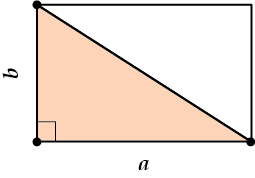
Прямоугольный треугольник
\( \displaystyle \Large S=\frac{1}{2}ab\)
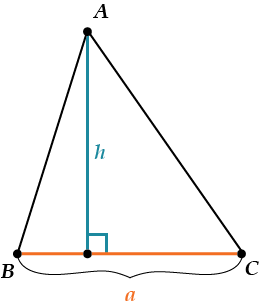
Произвольный треугольник
\( \displaystyle \Large S=\frac{1}{2}ah\)
Произвольный четырехугольник
\( \displaystyle \Large S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\cdot \sin \varphi \)
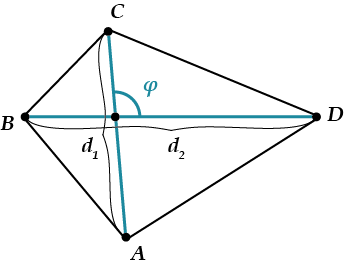
Понятие площади
Давай начнем с самого простого. За основу берется тот факт, что:
Площадь квадрата со стороной, равной \( \displaystyle \mathbf{1}\) единице длины, равна \( \displaystyle \mathbf{1}\) единице площади.

Другими словами, площадь квадрата со стороной \( \displaystyle \mathbf{1}\) метр мы считаем одним «метром площади».
Но писать все время «метр площади» и слишком длинно, и звучит как-то странно. И вот, математики придумали название «метр квадратный» и обозначение «\( \displaystyle {{м}^{2}}\)»
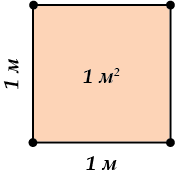
Посмотри внимательно на картинку и убедись, что там действительно нарисован – «метр квадратный»! И запомни обозначение.
А вот теперь хитрый вопрос: а что такое \( \displaystyle 2{{м}^{2}}\)? Площадь квадрата со стороной \( \displaystyle 2м\)?
А вот и нет!
Смотри: квадрат со стороной \( \displaystyle 2м\).
Пересчитай-ка, сколько в нем квадратных метров?
Удивительно, но получается \( \displaystyle 4\)!
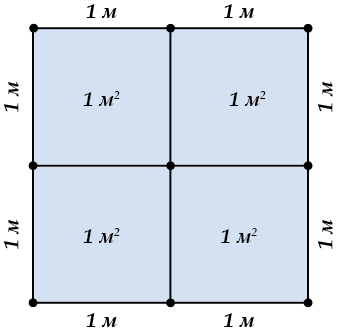
А чтобы получить \( \displaystyle 2\) квадратных метра (то есть, \( \displaystyle 2{{м}^{2}}\)), мы должны нарисовать, например так:
Видишь, здесь действительно нарисовано \( \displaystyle 2\) квадратных метра?
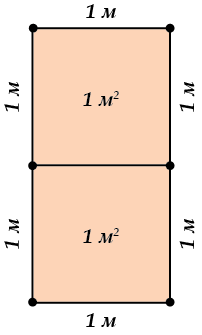
А как получить, скажем, \( \displaystyle 6{{м}^{2}}\)? Ну например так:
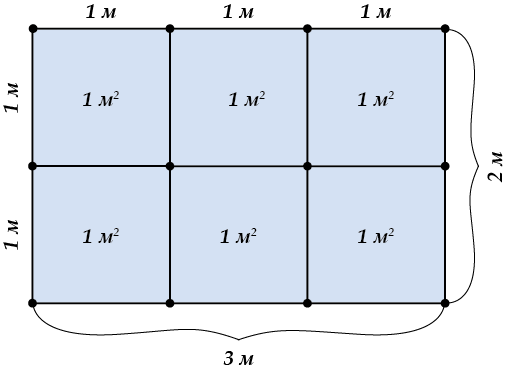
Да и вообще, если мы возьмем прямоугольник, у которого стороны равны \( \displaystyle a\) метров и \( \displaystyle b\) метров, то в этом прямоугольнике…
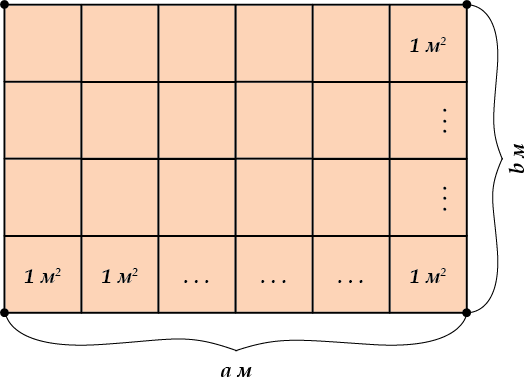
…поместится ровно \( \displaystyle a\cdot b\) квадратных метров. Посмотри внимательно: у нас есть \( \displaystyle b\) «слоев», в каждом из которых ровно \( \displaystyle a\) квадратных метров.
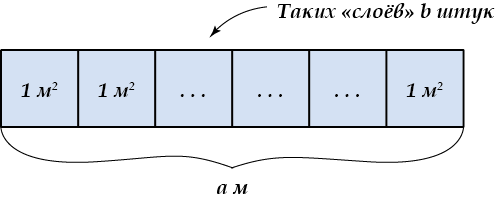
Значит, всего в прямоугольнике размером \( \displaystyle a\)x\( \displaystyle b\) поместилось \( \displaystyle ab\) квадратных метров. Вот это число, сколько квадратных метров поместилось в прямоугольнике, и есть его площадь.
А если фигура – вовсе не прямоугольник, а какая-то абракадабра?
Можно ли узнать, сколько квадратных метров в ней находится? Можно ведь некоторые квадратные метры «порезать», переставить и т.д. ?..
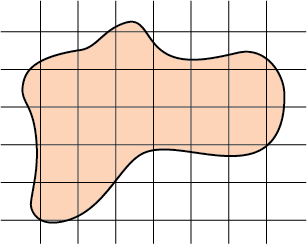
Удивлю тебя – бывают такие ужасные абракадабры, для которых совершенно невозможно установить сколько там квадратных метров. Даже приблизительно! К сожалению, нарисовать такие фигуры – невозможно.
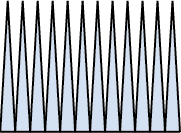
Но они есть! Они похожи, например, на такую «расческу» с очень мелкими зубьями.
Но мы такими «расческами» орудовать не будем, а будем рассматривать нормальные фигуры.
И вот, для нормальных фигур можно интуитивно (то есть для себя) считать, что площадь фигуры – это такое число, сколько в этой фигуре «поместится» квадратных единиц (метров, сантиметров и т.д.)
И представь себе, математики для многих фигур научились выражать площади через какие-то линейные (те, что можно измерить линейкой) элементы фигур. Эти выражения называются «формулы площади».
Формул этих довольно много – математики долго старались. Ты постарайся запомнить сначала самые простые и основные формулы, а потом уже те, что посложнее.
Формулы площади
Квадрат
\( \displaystyle \Large S={{a}^{2}}\) – это просто, не правда ли?

Прямоугольник
\( \displaystyle \Large S=ab\) – это мы уже успели обсудить.

Прямоугольный треугольник
Прямоугольный треугольник – ровно половина прямоугольника!
Поэтому:
\( \displaystyle \Large S=\frac{1}{2}ab\)
\( \displaystyle a\), \( \displaystyle b\) – катеты.

Произвольный треугольник
Для треугольника есть сразу несколько формул площади.
Основная формула
\( \displaystyle \Large S=\frac{1}{2}ah\)\( \displaystyle a\) – любая сторона,
\( \displaystyle h\) – высота к этой стороне.

Вторая основная формула
\( \displaystyle \Large S=\frac{1}{2}ab\cdot \sin \alpha \)\( \displaystyle a\), \( \displaystyle b\) – любые две стороны,
\( \displaystyle \alpha \) – угол между ними.
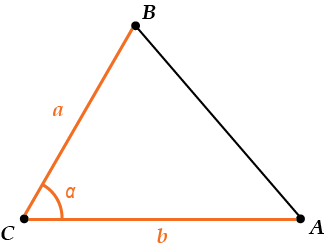
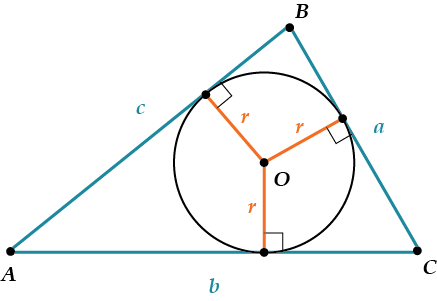
Третья формула
\( \displaystyle \Large S=pr\)\( \displaystyle p=\frac{a+b+c}{2}\) – полупериметр,
\( \displaystyle r\) – радиус вписанной окружности.
Еще одна невероятно полезная…
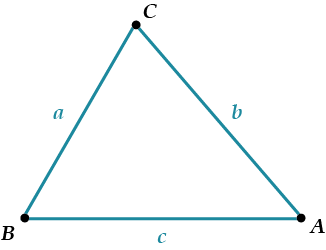
Формула Герона
\( \displaystyle S=\sqrt{p(p-a)(p-b)(p-c)}\)\( \displaystyle a\),\( \displaystyle b\),\( \displaystyle c\) – стороны,
\( \displaystyle p=\frac{a+b+c}{2}\) – полупериметр.
Какую же формулу выбрать для твоей задачки? Основными являются формулы 1 и 2. Третью формулу нужно применять, если тебе все дано: и три стороны, и радиус вписанной окружности. Но так ведь не бывает, верно?
Поэтому формулу 3 мы используем, скорее наоборот, для нахождения радиуса вписанной окружности. Тогда нужно найти площадь по одной из формул 1, 2 или 4, а потом уже радиус: \( \displaystyle r=\frac{S}{p}\).
Ну и формула 4 позволяет по \( \displaystyle 3\)-м сторонам с помощью длиннющей арифметики находить площадь. И не ошибайся в арифметике, когда будешь применять формулу Герона!
Произвольный четырехугольник
\( \displaystyle \Large S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\cdot \sin \varphi \)\( \displaystyle {{d}_{1}}; {{d}_{2}}\) – диагонали
\( \displaystyle \varphi \) – угол между ними
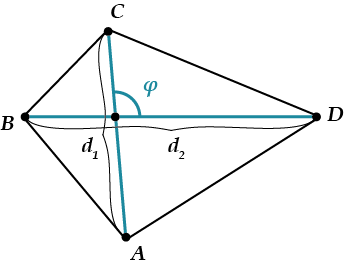
Для произвольного четырехугольника больше ничего нет, а вот для «хороших» четырехугольников – есть другие формулы.
(Многие из которых, кстати, на этой формуле и основываются!)
Параллелограмм
Основная формула
\( \displaystyle \Large S=ah\)\( \displaystyle a\) – любая сторона,
\( \displaystyle h\) – высота, опущенная на эту (!) cторону
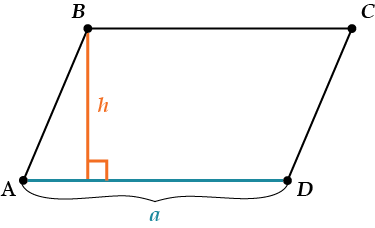
Вторая формула
И, как для всякого четырехугольника:
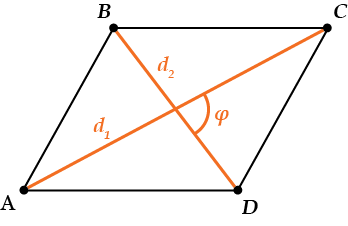
\( \displaystyle \Large S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\cdot \sin \varphi \)\( \displaystyle {{d}_{1}}; {{d}_{2}}\) – диагонали,
\( \displaystyle \varphi \) – угол между ними.
Ромб
У ромба диагонали перпендикулярны, поэтому основной для него становится формула:
\( \displaystyle \Large S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\)– и никакого \( \displaystyle \sin \varphi \) потому что \( \displaystyle \varphi =90^o\), и \( \displaystyle sin90^o=1\)
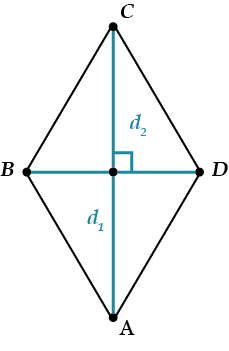
\( \displaystyle {{d}_{1}}; {{d}_{2}}\) – как всегда, диагонали
Вторая формула
А дополнительной формулой становится:
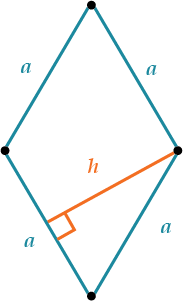
\( \displaystyle \Large S=ah\)\( \displaystyle a\) – сторона,
\( \displaystyle h\) – высота, опущенная на cторону.
Трапеция
Основная формула
\( \displaystyle \Large S=\frac{a+b}{2}\cdot h\)\( \displaystyle a,b\) – основания,
\( \displaystyle h\) – высота.
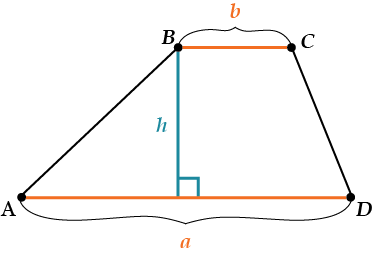
Вторая формула
\( \displaystyle \Large S=\frac{1}{2}{{d}_{1}}{{d}_{2}}\cdot \sin \varphi \) – ведь трапеция – тоже четырехугольник.
\( \displaystyle {{d}_{1}}; {{d}_{2}}\) – диагонали,
\( \displaystyle \varphi \) – угол между ними.
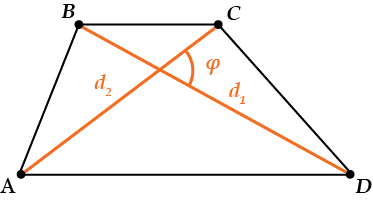
Хитрые вопросы о площадях
Кроме задачек, в которых просят просто найти площадь, встречаются еще всякие вопросики.
Ну вот например:
Во сколько раз увеличится площадь квадрата, если его сторону увеличить в три раза?
Давай ответим на этот вопрос двумя способами.
Первый способ – формальный: используем формулу площади квадрата.
Итак, было \( \displaystyle S_{старого}={{a}^{2}}\), значит \( \displaystyle S_{нового}=({3a})^{2}=9{a}^{2}\) – площадь увеличилась в \( \displaystyle 9\) раз!
В случае с квадратами есть и второй способ «пощупать» и убедиться напрямую в этом числе \( \displaystyle 9\).
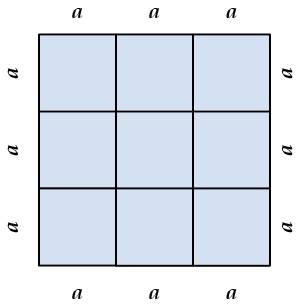
Рисуем:
Видишь, в квадрате со стороной \( \displaystyle 3a\) уместилось ровно \( \displaystyle 9\) квадратов со стороной \( \displaystyle a\).
Значит, формулам действительно можно верить 🙂
Если же у тебя не квадрат, то остается только подставлять новые значения в формулы – и не удивляйся, если вдруг числа получатся довольно большими.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


