Производная функции — геометрический смысл и правила дифференцирования
Задачи на производную функции на ЕГЭ незаслуженно считаются сложными.
Они будут сложными в институте, но в школе это не так. На этой теме можно легко получить хорошие баллы на ЕГЭ.
Если вы не понимаете смысл производной или не умеете ее находить, для вас этот пост.
Прочитайте его и вы сможете решить любую задачу на производную функции на ЕГЭ.
Производная функции — коротко о главном
Определение производной
Производная функции – отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента:
\( \displaystyle {f}’\left( x \right)=\frac{\Delta f}{\Delta x}\) при \( \displaystyle \Delta x\to 0\)
Базовые производные
Правила дифференцирования
- Константа выносится за знак производной: \( \displaystyle {{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’\)
- Производная суммы: \( \displaystyle {{\left( f+y \right)}^{\prime }}={f}’+{y}’\)
- Производная произведения: \( \displaystyle {{\left( f\cdot y \right)}^{\prime }}={f}’\cdot y+f\cdot {y}’\)
- Производная частного: \( \displaystyle {{\left( \frac{f}{y} \right)}^{\prime }}=\frac{{f}’y-f{y}’}{{{y}^{2}}}\)
- Производная сложной функции: \( \displaystyle {{\left[ f\left( y \right) \right]}^{\prime }}={f}’\left( y \right)\cdot {y}’\)
Алгоритм нахождения производной от сложной функции
- Определяем «внутреннюю» функцию, находим ее производную.
- Определяем «внешнюю» функцию, находим ее производную.
- Умножаем результаты первого и второго пунктов.
Геометрический смысл производной
Основная причина почему ты не умеешь решать задачи на производную — это непонимание ее сути. Ты просто не понимаешь что это такое!
А между прочим производная — это очень интересная, полезная и… довольно простая штука.
Не веришь?
Читай этот раздел.
Представим себе прямую дорогу, проходящую по холмистой местности. То есть она идет то вверх, то вниз, но вправо или влево не поворачивает.
Если ось \( Ox\) направить вдоль дороги горизонтально, а \( Oy\) – вертикально, то линия дороги будет очень похожа на график какой-то непрерывной функции:
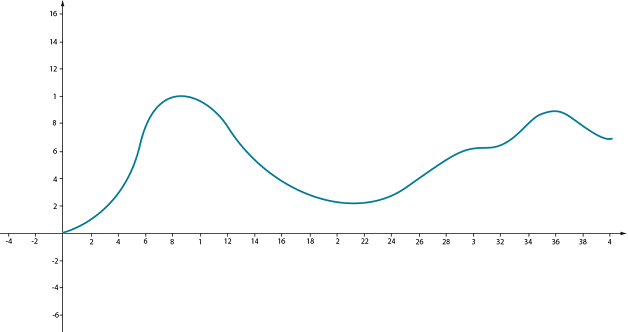
Ось \( Ox\) – это некий уровень нулевой высоты, в жизни мы используем в качестве него уровень моря. Двигаясь вперед по такой дороге, мы также движемся вверх или вниз.
Также мы можем сказать: при изменении аргумента (продвижение вдоль оси абсцисс) изменяется значение функции (движение вдоль оси ординат).
А теперь давай подумаем, как определить «крутизну» нашей дороги? Что это может быть за величина?
Очень просто: на сколько изменится высота при продвижении вперед на определенное расстояние.
Ведь на разных участках дороги, продвигаясь вперед (вдоль оси абсцисс) на один километр, мы поднимемся или опустимся на разное количество метров относительно уровня моря (вдоль оси ординат).
Продвижение вперед обозначим \( \displaystyle \Delta x\) (читается «дельта икс»).
Греческую букву \( \displaystyle \Delta \) (дельта) в математике обычно используют как приставку, означающую «изменение».
То есть \( \displaystyle \Delta x\) – это изменение величины \( \displaystyle x\), \( \displaystyle \Delta y\) – изменение \( \displaystyle y\); тогда что такое \( \displaystyle \Delta f\)? Правильно, изменение величины \( \displaystyle f\).
Важно: выражение \( \displaystyle \Delta x\) – это единое целое, одна переменная. Никогда нельзя отрывать «дельту» от «икса» или любой другой буквы!
То есть, например, \( \displaystyle \frac{\Delta x}{\Delta y}\ne \frac{x}{y}\)
Итак, мы продвинулись вперед, по горизонтали, на \( \displaystyle \Delta x\). Если линию дороги мы сравниваем с графиком функции \( \displaystyle f\left( x \right)\), то как мы обозначим подъем?
Конечно, \( \displaystyle \Delta f\). То есть, при продвижении вперед на \( \displaystyle \Delta x\) мы поднимаемся выше на \( \displaystyle \Delta f\).
Величину \( \displaystyle \Delta f\) посчитать легко: если в начале мы находились на высоте \( \displaystyle {{f}_{1}}\), а после перемещения оказались на высоте \( \displaystyle {{f}_{2}}\), то \( \displaystyle \Delta f={{f}_{2}}-{{f}_{1}}\).
Если конечная точка оказалась ниже начальной, \( \displaystyle \Delta f\) будет отрицательной – это означает, что мы не поднимаемся, а спускаемся.
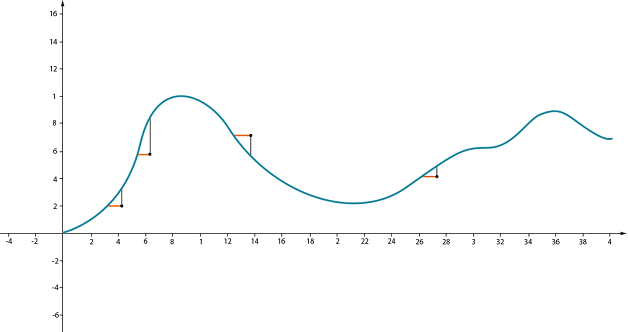
Вернемся к «крутизне»: это величина, которая показывает, насколько сильно (круто) увеличивается высота при перемещении вперед на единицу расстояния:
\( \displaystyle K=\frac{\Delta f}{\Delta x}\).
Предположим, что на каком-то участке пути при продвижении на \( 1\) км дорога поднимается вверх на \( 1\) км. Тогда крутизна в этом месте равна \( 1\).
А если дорога при продвижении на \( 100\) м опустилась на \( 0,5\)км?
Тогда крутизна равна \( \displaystyle K=\frac{-\text{500м}}{\text{100м}}=-5\).
А теперь рассмотрим вершину какого-нибудь холма.
Если взять начало участка за полкилометра до вершины, а конец – через полкилометра после него, видно, что высота практически одинаковая.
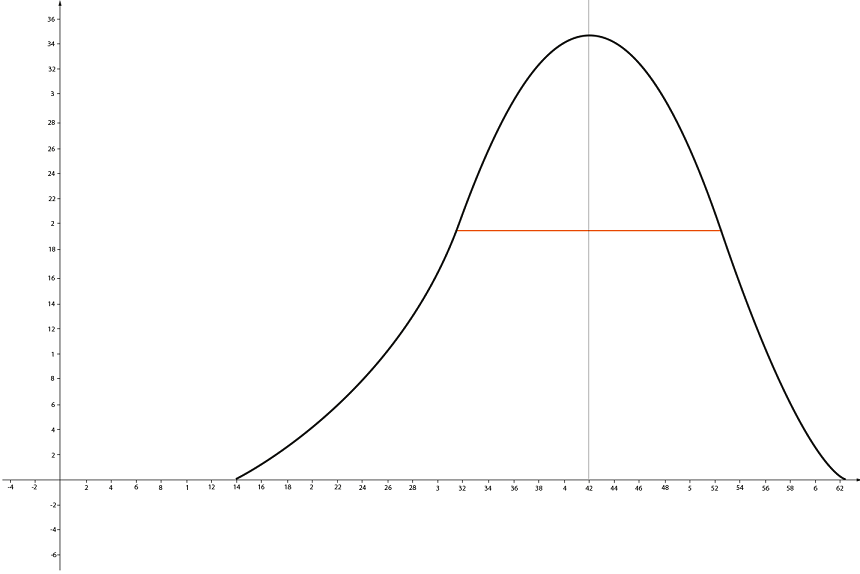
То есть, по нашей логике выходит, что крутизна здесь почти равна нулю, что явно не соответствует действительности.
Просто на расстоянии в \( 1\) км может очень многое поменяться.
Нужно рассматривать более маленькие участки для более адекватной и точной оценки крутизны.
Например, если измерять изменение высоты при перемещении на один метр, результат будет намного точнее. Но и этой точности нам может быть недостаточно – ведь если посреди дороги стоит столб, мы его можем просто проскочить.
Какое расстояние тогда выберем? Сантиметр? Миллиметр?
Чем меньше, тем лучше!
В реальной жизни измерять расстояние с точностью до миллиметра – более чем достаточно. Но математики всегда стремятся к совершенству.
Поэтому было придумано понятие бесконечно малого, то есть величина по модулю меньше любого числа, которое только можем назвать.
Например, ты скажешь: одна триллионная! Куда уж меньше?
А ты подели это число на \( 2\) – и будет еще меньше. И так далее.
Если хотим написать, что величина \( x\) бесконечно мала, пишем так: \( \displaystyle x\to 0\) (читаем «икс стремится к нулю»).
Очень важно понимать, что это число не равно нулю! Но очень близко к нему. Это значит, что на него можно делить.
Понятие, противоположное бесконечно малому – бесконечно большое (\( \displaystyle x\to \infty \)).
Ты уже наверняка сталкивался с ним, когда занимался неравенствами: это число по модулю больше любого числа, которое только можешь придумать.
Если ты придумал самое большое из возможных чисел, просто умножь его на два, и получится еще больше. А бесконечность еще больше того, что получится.
Фактически бесконечно большое и бесконечно малое обратны друг другу, то есть при \( \displaystyle x\to 0:\text{ }\frac{1}{x}\to \infty \), и наоборот: при \( \displaystyle x\to \infty :\text{ }\frac{1}{x}\to 0\).
Теперь вернемся к нашей дороге.
Идеально посчитанная крутизна – это крутизна, вычисленная для бесконечно малого отрезка пути, то есть:
\( \displaystyle K=\frac{\Delta f}{\Delta x}\text{ при }\Delta x\to 0\).
Замечу, что при бесконечно малом перемещении изменение высоты тоже будет бесконечно мало.
Но напомню, бесконечно малое – не значит равное нулю. Если поделить друг на друга бесконечно малые числа, может получиться вполне обычное число.
Например, \( \displaystyle 2\). То есть одна малая величина может быть ровно в \( \displaystyle 2\) раза больше другой.
К чему все это?
Дорога, крутизна… Мы ведь не в автопробег отправляемся, а математику учим. А в математике все точно так же, только называется по-другому.
Давай посмотрим как.
Понятие производной функции
А сейчас мы изучим основные математические термины и продолжим изучение производной.
Раздел тоже не сложный. Просто будь внимателен.
Поехали!
Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращение аргумента.
Приращением в математике называют изменение.
То, насколько изменился аргумент (\( \displaystyle x\)) при продвижении вдоль оси \( \displaystyle Ox\), называется приращением аргумента и обозначается \( \displaystyle \Delta x.\)
То, насколько изменилась функция (высота) при продвижении вперед вдоль оси \( \displaystyle Ox\) на расстояние \( \displaystyle \Delta x\), называется приращением функции и обозначается \( \displaystyle \Delta f\).
Итак, производная функции \( \displaystyle f\left( x \right)\) – это отношение \( \displaystyle \Delta f\) к \( \displaystyle \Delta x\) при \( \displaystyle \Delta x\to 0\).
Обозначаем производную той же буквой, что и функцию, только со штрихом сверху справа: \( \displaystyle {f}’\left( x \right)\) или просто \( \displaystyle {f}’\).
Итак, запишем формулу производной, используя эти обозначения:
\( \displaystyle {f}’\left( x \right)=\frac{\Delta f}{\Delta x}\text{ при}\ \Delta x\to 0\)
А бывает ли производная равна нулю?
Как и в аналогии с дорогой здесь при возрастании функции производная положительна, а при убывании – отрицательна.
Конечно. Например, если мы едем по ровной горизонтальной дороге, крутизна равна нулю. И правда, высота ведь не совсем меняется. Так и с производной: производная постоянной функции (константы) равна нулю:
\( \displaystyle {C}’=0,\text{ }C=const\),
так как приращение такой функции равно нулю при любом \( \Delta x\).
А еще?
Давай вспомним пример с вершиной холма. Там получалось, что можно так расположить концы отрезка по разные стороны от вершины, что высота на концах оказывается одинаковой, то есть отрезок располагается параллельно оси \( Ox\):

Но большие отрезки – признак неточного измерения. Будем поднимать наш отрезок вверх параллельно самому себе, тогда его длина будет уменьшаться.
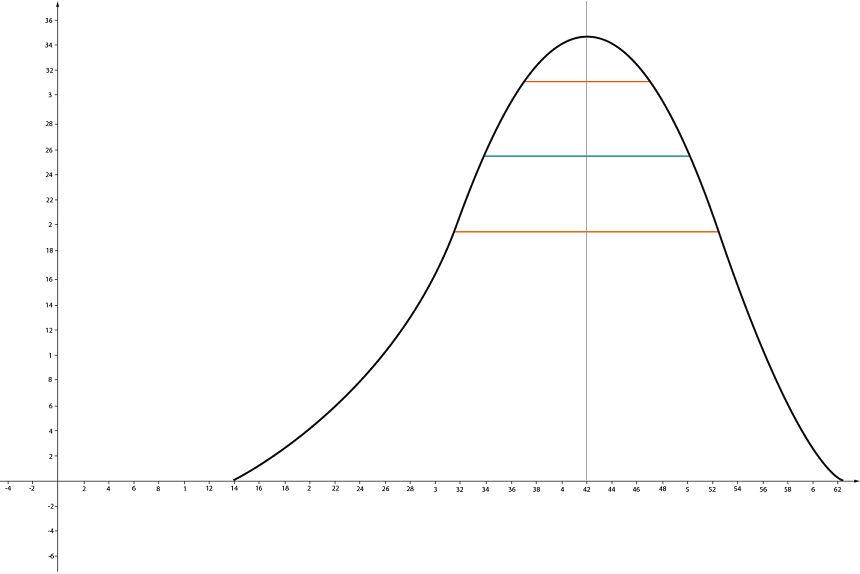
В конце концов, когда мы будем бесконечно близко к вершине, длина отрезка станет бесконечно малой.
Но при этом он остался параллелен оси \( Ox\), то есть разность высот на его концах \( \displaystyle \Delta f\) равна нулю (не стремится, а именно равна).
Значит, производная
\( \displaystyle {f}’\left( {{x}_{\text{вершины}}} \right)=\frac{\Delta f}{\Delta x}=\frac{0}{\Delta x}=0\).
Понять это можно так: когда мы стоим на самой вершине, меленькое смещение влево или вправо изменяет нашу высоту ничтожно мало.
Есть и чисто алгебраическое объяснение: левее вершины функция возрастает, а правее – убывает.
Как мы уже выяснили ранее, при возрастании функции производная положительна, а при убывании – отрицательна.
Но меняется она плавно, без скачков (т.к. дорога нигде не меняет наклон резко).
Поэтому между отрицательными и положительными значениями обязательно должен быть \( \displaystyle 0\). Он и будет там, где функция ни возрастает, ни убывает – в точке вершины.
То же самое справедливо и для впадины (область, где функция слева убывает, а справа – возрастает):
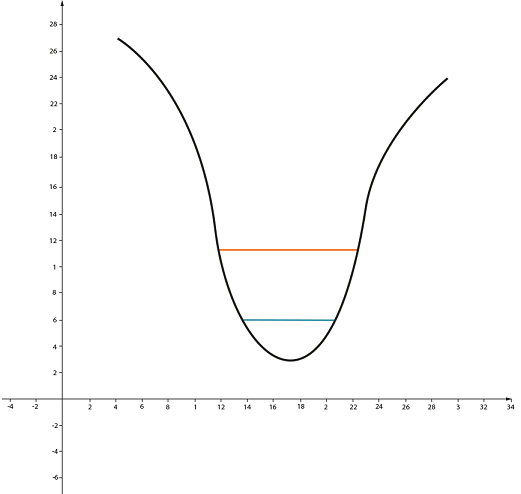
Приращение функции
А теперь немного подробнее о приращениях…
Мы уже ввели это понятие и чтобы закрепить его, давай решим несколько примеров.
Пробуй решать до того, как посмотришь как мы это сделали!
Итак, мы меняем аргумент на величину \( \Delta x\).
Меняем от какого значения?
Каким он (аргумент) теперь стал?
Можем выбрать любую точку, и сейчас будем от нее плясать.
Рассмотрим точку с координатой \( \displaystyle {{x}_{0}}\). Значение функции в ней равно \( f\left( {{x}_{0}} \right)\).
Затем делаем то самое приращение: увеличиваем координату \( {{x}_{0}}\) на \( \Delta x\).
Чему теперь равен аргумент?
Очень легко: \( {{x}_{0}}+\Delta x\).
А чему теперь равно значение функции?
Куда аргумент, туда и функция: \( f\left( {{x}_{0}}+\Delta x \right)\).
А что с приращением функции?
Ничего нового: это по-прежнему величина, на которую изменилась функция:
\( \Delta f=f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)\).
2 примера на тренировку
- Найди приращение функции \( \displaystyle f\left( x \right)=2x+3\) в точке \( {{x}_{0}}=2\) при приращении аргумента, равном \( \Delta x\);
- То же самое для функции \( y\left( x \right)={{x}^{2}}+2{x} -1\) в точке \( {{x}_{0}}=1\).
Решения:
Потренируемся брать производные
Ну ладно, ладно, уже давно понятно, что такое производная!
Но как ее применить на практике?
Давайте уже возьмем и вычислим какую-нибудь производную, в конце концов!
Щас все будет 🙂
Производная константы
Это мы уже обсуждали: если функция \( y=f\left( x \right)=c\), где \( c\) – некое постоянное число, то каким бы ни было приращение аргумента \( \Delta x\), функция нисколько не изменяется: \( \Delta f=0\). А значит,
\( \displaystyle {f}’\left( x \right)={c}’=\frac{\Delta f}{\Delta x}=0\)То есть,
Производная от константы равна нулю: \( {c}’=0\)
Производные степенной функции
Степенной называют функцию, где аргумент в какой-то степени (логично, да?).
Причем – в любой степени: \( f\left( x \right)={{x}^{a}},\text{ }a\in \mathbb{R}\).
Производная функции первой степени
Простейший случай – это когда показатель степени \( a=1\):
\( f\left( x \right)=x\).
Найдем ее производную в точке \( {{x}_{0}}\). Вспоминаем определение производной:
\( {f}’\left( {{x}_{0}} \right)=\frac{\Delta f}{\Delta x}\)
Итак, аргумент меняется с \( {{x}_{0}}\) до \( {{x}_{0}}+\Delta x\). Каково приращение функции?
Приращение – это \( \Delta f=f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)\). Но функция в любой точке равна своему аргументу.
Поэтому:
\( \Delta f=\left( {{x}_{0}}+\Delta x \right)-{{x}_{0}}=\Delta x\).
Производная равна:
\( {f}’\left( {{x}_{0}} \right)=\frac{\Delta f}{\Delta x}=\frac{\Delta x}{\Delta x}=1\)Производная от \( \displaystyle x\) равна \( \displaystyle 1\): \( \displaystyle {x}’=1\)
Производная квадратичной функции
Теперь рассмотрим квадратичную функцию (\( \displaystyle a=2\)): \( f\left( x \right)={{x}^{2}}\).
\( \displaystyle \begin{array}{l}\Delta f=f\left( x+\Delta x \right)-f\left( x \right)=\underbrace{{{\left( x+\Delta x \right)}^{2}}}_{f\left( x+\Delta x \right)}-\underbrace{{{x}^{2}}}_{f\left( x \right)}=\\={{x}^{2}}+2x\Delta x+\Delta {{x}^{2}}-{{x}^{2}}=2x\cdot \Delta x+\Delta {{x}^{2}}\end{array}\)
\( {f}’\left( x \right)=\frac{\Delta f}{\Delta x}=\frac{2x\Delta x+\Delta {{x}^{2}}}{\Delta x}=2x+\Delta x\).
А теперь вспомним, что \( \Delta x\to 0\). Это значит, что значением приращения можно пренебречь, так как оно бесконечно мало, и поэтому незначительно на фоне другого слагаемого:
\( {f}’\left( x \right)=2x\).
Итак, у нас родилось очередное правило:
\( {{\left( {{x}^{2}} \right)}^{\prime }}=2x\)
Производная функции третьей степени
Продолжаем логический ряд: \( f\left( x \right)={{x}^{3}}\).
\( \Delta f=f\left( x+\Delta x \right)-f\left( x \right)=\underbrace{{{\left( x+\Delta x \right)}^{3}}}_{f\left( x+\Delta x \right)}-\underbrace{{{x}^{3}}}_{f\left( x \right)}.\)Это выражение можно упростить по-разному: раскрыть первую скобку по формуле сокращенного умножения куб суммы, или же разложить все выражение на множители по формуле разности кубов.
Попробуй сделать это сам любым из предложенных способов.
Итак, у меня получилось следующее:
\( \displaystyle \begin{array}{l}\Delta f=f\left( x+\Delta x \right)-f\left( x \right)={{\left( x+\Delta x \right)}^{3}}-{{x}^{3}}=\left( x+\Delta x-x \right)\cdot \\\cdot \left( {{\left( x+\Delta x \right)}^{2}}+\left( x+\Delta x \right)\cdot x+{{x}^{2}} \right)=\Delta x\left( 3{{x}^{2}}+3x\Delta x+\Delta {{x}^{2}} \right)\end{array}\)
\( {f}’\left( x \right)=\frac{\Delta f}{\Delta x}=\frac{\Delta x\left( 3{{x}^{2}}+3x\Delta x+\Delta {{x}^{2}} \right)}{\Delta x}=3{{x}^{2}}+3x\Delta x+\Delta {{x}^{2}}\).
И снова вспомним, что \( \Delta x\to 0\). Это значит, что можно пренебречь всеми слагаемыми, содержащими \( \Delta x\):
\( {f}’\left( x \right)=3{{x}^{2}}\)
Получаем:
\( {{\left( {{x}^{3}} \right)}^{\prime }}=3{{x}^{2}}\)
Производная функции больших степеней
Аналогичные правила можно получить и для больших степеней:
\( \begin{array}{l}{{\left( {{x}^{4}} \right)}^{\prime }}=4{{x}^{3}}\\{{\left( {{x}^{5}} \right)}^{\prime }}=5{{x}^{4}}\\{{\left( {{x}^{6}} \right)}^{\prime }}=6{{x}^{5}}\\…\\{{\left( {{x}^{n}} \right)}^{\prime }}=n{{x}^{n-1}}\end{array}\)Оказывается, это правило можно обобщить для степенной функции с произвольным показателем, даже не целым:
\( {{\left( {{x}^{a}} \right)}^{\prime }}=a{{x}^{a-1}},\text{ }a\in \mathbb{R}\) (2)
Можно сформулировать правило словами: «степень выносится вперед как коэффициент, а потом уменьшается на \( \displaystyle 1\)».
Докажем это правило позже (почти в самом конце). А сейчас рассмотрим несколько примеров.
Три примера на тренировку
Пример 1
\( y=\sqrt{x}\).
Пример 2
\( y=\frac{1}{x}\).
Пример 3
\( f=\frac{1}{\sqrt[3]{x}}\).
Решения:
Производная тригонометрических функций
Здесь будем использовать один факт из высшей математики:
При \( x\to 0\) выражение \( \frac{\sin x}{x}\to 1\).
Доказательство ты узнаешь на первом курсе института (а чтобы там оказаться, надо хорошо сдать ЕГЭ 😉 ).
Сейчас только покажу это графически:
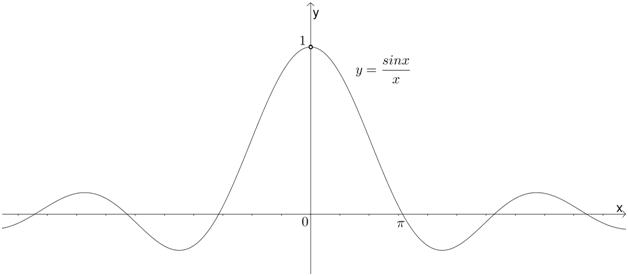
Видим, что при \( \displaystyle x=0\) функция не существует – точка на графике выколота. Но чем ближе \( \displaystyle x\) к значению \( \displaystyle0\), тем ближе функция к \( \displaystyle 1\). Это и есть то самое «стремится».
Впредь будем считать, что при \( x\to 0\) это выражение равно \( \displaystyle 1\): \( \frac{\sin x}{x}=1\).
Дополнительно можешь проверить это правило с помощью калькулятора. Да-да, не стесняйся, бери калькулятор, мы ведь не на ЕГЭ еще.
Итак, пробуем: \( x=0,1:\text{ }\frac{\sin x}{x}=\frac{\sin 0,1}{0,1}\approx 0,9983\);
Не забудь перевести калькулятор в режим «Радианы»!
Попробуй теперь сам для \( \displaystyle x\text{ }=\text{ }0,01;\text{ }0,001;\text{ }0,0001\) и так далее.
\( \frac{\sin 0,01}{0,01}\approx 0,999983…;\text{ }\frac{\sin 0,001}{0,001}\approx 0,99999983…\) и т.д. Видим, что чем меньше \( \displaystyle x\), тем ближе значение отношения к \( \displaystyle 1\).
Убедился? Идем дальше.
Производная синуса
Рассмотрим функцию \( y=\sin x\). Как обычно, найдем ее приращение:
\( \Delta y=\sin \left( x+\Delta x \right)-\sin x\).
Превратим разность синусов в произведение.
Для этого используем формулу (вспоминаем тему «Формулы тригонометрии»): \( \sin \alpha -\sin \beta =2\sin \frac{\alpha -\beta }{2}\cdot \cos \frac{\alpha +\beta }{2}\).
\( \Delta y=\sin \left( x+\Delta x \right)-\sin x=2\sin \frac{x+\Delta {x} -x}{2}\cdot \cos \frac{x+\Delta x+x}{2}=2\sin \frac{\Delta x}{2}\cdot \cos \left( x+\frac{\Delta x}{2} \right)\)Теперь производная:
\( {y}’=\frac{\Delta y}{\Delta x}=\frac{2\sin \frac{\Delta x}{2}\cdot \cos \left( x+\frac{\Delta x}{2} \right)}{\Delta x}=\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}\cdot \cos \left( x+\frac{\Delta x}{2} \right)\).
Сделаем замену: \( t=\frac{\Delta x}{2}\).
Тогда при бесконечно малом \( \Delta x\text{ }\left( \Delta x\to 0 \right)\) \( \displaystyle t\) также бесконечно мало: \( t\to 0\). Выражение для \( \displaystyle {y}’\) принимает вид:
\( {y}’=\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}\cdot \cos \left( x+\frac{\Delta x}{2} \right)=\frac{\sin t}{t}\cdot \cos \left( x+t \right)\).
А теперь вспоминаем, что при \( t\to 0\) выражение \( \frac{\sin t}{t}=1\). А также, что если бесконечно малой величиной \( \displaystyle t\) можно пренебречь в сумме \( x+t\) (то есть \( x+t\to x\) при \( t\to 0\)).
\( {y}’=\underbrace{\frac{\sin t}{t}}_{\to \text{1}}\cdot \cos \underbrace{\left( x+t \right)}_{\to x}=1\cdot \cos x=\cos x\).
Итак, получаем следующее правило:
Производная синуса равна косинусу: \( {{\left( \sin x \right)}^{\prime }}=\cos x\)
Производная косинуса
Теперь косинус: \( y\left( x \right)=\cos x\). Здесь будем использовать формулу разности косинусов: \( \cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\cdot \sin \frac{\alpha -\beta }{2}\):
\( \Delta y=\cos \left( x+\Delta x \right)-\cos x=-2\sin \frac{x+\Delta x+x}{2}\cdot \sin \frac{x+\Delta {x} -x}{2}=-2\sin \left( x+\frac{\Delta x}{2} \right)\cdot \sin \frac{\Delta x}{2}\).
\( {y}’=\frac{\Delta y}{\Delta x}=\frac{-2\sin \left( x+\frac{\Delta x}{2} \right)\cdot \sin \frac{\Delta x}{2}}{\Delta x}=-\sin \underbrace{\left( x+\frac{\Delta x}{2} \right)}_{x}\cdot \underbrace{\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}}_{1}=-\sin x\).
Значит, производная косинуса равна минус синусу: \( {{\left( \cos x \right)}^{\prime }}=-\sin x\)
Это базовые («табличные») производные. Вот они одним списком:
\( \displaystyle \begin{array}{l}{c}’=0\\{{\left( {{x}^{a}} \right)}^{\prime }}=a\cdot {{x}^{a-1}}\text{ }\left( a\in \mathbb{R} \right)\\{{\left( \sin x \right)}^{\prime }}=\cos x\\{{\left( \cos x \right)}^{\prime }}=-\sin x\end{array}\)Три примера на тренировку
- Найди производную функции \( f\left( x \right)=\cos x\) в точке \( {{x}_{0}}=-\frac{\pi }{6}\);
- Найди производную функции \( f\left( x \right)=\frac{{{x}^{3}}}{\sqrt[5]{{{x}^{2}}}}\) в точке \( {{x}_{0}}=1\);
- Найди производную функции \( f\left( x \right)={{x}^{4}}\sin \left( \sqrt[3]{2{{x}^{2}}+3}-1 \right)\).
Решения:
Производная экспоненты и натурального логарифма
Есть в математике такая функция, производная которой при любом \( \displaystyle x\) равна значению самой функции при этом же \( \displaystyle x\). Называется она «экспонента», и является показательной функцией
\( \displaystyle f\left( x \right)={{e}^{x}}\).
Основание этой функции – константа \( \displaystyle e\approx 2,7183…\) – это бесконечная десятичная дробь, то есть число иррациональное (такое как \( \displaystyle \pi \)). Его называют «число Эйлера», поэтому и обозначают буквой \( \displaystyle \mathbf{e}\).
Итак, правило:
\( \displaystyle {{\left( {{e}^{x}} \right)}^{\prime }}={{e}^{x}}\)
Запомнить очень легко.
Ну и не будем далеко ходить, сразу же рассмотрим обратную функцию. Какая функция является обратной для показательной функции? Логарифм:
\( \displaystyle y={{a}^{x}}\text{ }\Leftrightarrow \text{ }x={{\log }_{a}}y\)
В нашем случае основанием служит число \( \displaystyle \mathbf{e}\):
\( \displaystyle y={{e}^{x}}\text{ }\Leftrightarrow \text{ }x={{\log }_{e}}y\)
Такой логарифм (то есть логарифм с основанием \( \displaystyle \mathbf{e}\)) называется «натуральным», и для него используем особое обозначение \( \displaystyle \mathbf{ln}\): вместо \( \displaystyle {{\log }_{e}}x\) пишем \( \displaystyle \ln x\).
Чему равен \( \displaystyle \ln \left( {{e}^{a}} \right)\)? Конечно же, \( \displaystyle a\).
Производная от натурального логарифма тоже очень простая:
\( \displaystyle {{\left( \ln x \right)}^{\prime }}=\frac{1}{x}\)Два примера на тренировку
- Найди производную функции \( \displaystyle {{e}^{x+5}}\).
- Чему равна производная функции \( \displaystyle \ln \left( x+1 \right)\)?
Решения:
7 важнейших правил дифференцирования (или правил нахождения производной)
Правила чего? Опять новый термин, опять?!…
Дифференцирование – это процесс нахождения производной.
Только и всего. А как еще назвать этот процесс одним словом? Не производнование же…
Дифференциалом математики называют то самое приращение функции \( \displaystyle \Delta f\) при \( \displaystyle \Delta x\to 0\).
Происходит этот термин от латинского differentia — разность. Вот.
При выводе всех этих правил будем использовать две функции, например, \( \displaystyle f\) и \( \displaystyle y\). Нам понадобятся также формулы их приращений:
\( \displaystyle \begin{array}{l}\Delta f=f\left( x+\Delta x \right)-f\left( x \right)\text{ }\Rightarrow \text{ }f\left( x+\Delta x \right)=f\left( x \right)+\Delta f\\\Delta y=y\left( x+\Delta x \right)-y\left( x \right)\text{ }\Rightarrow \text{ }y\left( x+\Delta x \right)=y\left( x \right)+\Delta y\end{array}\)
Всего имеется 7 очень важных правил . Сейчас мы разберем каждое из них с примерами и подробными объяснениями!
1. Константа выносится за знак производной
Если \( \displaystyle c\) – какое-то постоянное число (константа), тогда.
\( \displaystyle {{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’\)
Это правило употребляется чаще всех. Докажем его:
Пусть \( \displaystyle y\left( x \right)=c\cdot f\left( x \right)\), или проще \( \displaystyle y=cf\).
\( \displaystyle \Delta y=y\left( x+\Delta x \right)-y\left( x \right)=cf\left( x+\Delta x \right)-cf\left( x \right)=c\underbrace{\left( f\left( x+\Delta x \right)-f\left( x \right) \right)}_{\text{Это}\ \text{же}\Delta f}=c\Delta f\).
\( \displaystyle {y}’=\frac{\Delta y}{\Delta x}=\frac{c\Delta f}{\Delta x}=c\cdot \underbrace{\frac{\Delta f}{\Delta x}}_{\text{Это }{f}’}=c\cdot {f}’\), ч.т.д.
Пример 1
Найдите производную функции \( \displaystyle y=3{{x}^{2}}\) в точке \( \displaystyle {{x}_{0}}=2\).
Ты сперва сам попробуй решить, а потом посмотри решение:
2. Производная суммы
Производная суммы равна сумме производных:
\( \displaystyle {{\left( f+y \right)}^{\prime }}={f}’+{y}’\)
Очевидно, это правило работает и для разности: \( \displaystyle {{\left( f-y \right)}^{\prime }}={f}’-{y}’\).
Докажем. Пусть \( \displaystyle g\left( x \right)=f\left( x \right)+y\left( x \right)\), или проще \( \displaystyle g=f+y\).
\( \displaystyle \begin{array}{l}\Delta g=g\left( x+\Delta x \right)-g\left( x \right)=\underbrace{\left( f\left( x+\Delta x \right)+y\left( x+\Delta x \right) \right)}_{g\left( x+\Delta x \right)}-\underbrace{\left( f\left( x \right)+y\left( x \right) \right)}_{g\left( x \right)}=\\\text{ }=\underline{f\left( x+\Delta x \right)}+\underline{\underline{y\left( x+\Delta x \right)}}-\underline{f\left( x \right)}-\underline{\underline{y\left( x \right)}}=\Delta f+\Delta y\\\end{array}\)
\( \displaystyle {g}’=\frac{\Delta g}{\Delta x}=\frac{\Delta f+\Delta y}{\Delta x}=\frac{\Delta f}{\Delta x}+\frac{\Delta y}{\Delta x}={f}’+{y}’\).
Четыре примера для тренировки (Найдите производные функций)
- \( \displaystyle y=2x+3\) в точке \( \displaystyle {{x}_{0}}=2\);
- \( \displaystyle f=3{{x}^{2}}+2{x} -5\) в точке \( \displaystyle {{x}_{0}}=0,2\);
- \( \displaystyle g={{x}^{3}}-3{{x}^{2}}-x\) в точке \( \displaystyle {{x}_{0}}=3\);
- \( \displaystyle y=\sin x+\cos x\) в точке \( \displaystyle {{x}_{0}}=\frac{3\pi }{4}\).
Решения:
3. Производная произведения
\( \displaystyle {{\left( f\cdot y \right)}^{\prime }}={f}’\cdot y+f\cdot {y}’\)
Хм, все сложнее и сложнее. Ну, давай разбираться.
Снова введем новую функцию: \( \displaystyle g\left( x \right)=f\left( x \right)\cdot y\left( x \right)\), или проще \( \displaystyle g=f\cdot y\).
\( \displaystyle \Delta g=g\left( x+\Delta x \right)-g\left( x \right)=f\left( x+\Delta x \right)\cdot y\left( x+\Delta x \right)-f\left( x \right)\cdot y\left( x \right)\).
Вспомним, о чем говорили в самом начале этого раздела:
\( \displaystyle \begin{array}{l}\Delta f=f\left( x+\Delta x \right)-f\left( x \right)\text{ }\Rightarrow \text{ }f\left( x+\Delta x \right)=f\left( x \right)+\Delta f\underset{\text{упрощенно}}{\mathop{=}}\,f+\Delta f\\\Delta y=y\left( x+\Delta x \right)-y\left( x \right)\text{ }\Rightarrow \text{ }y\left( x+\Delta x \right)=y\left( x \right)+\Delta y\underset{\text{упрощенно}}{\mathop{=}}\,y+\Delta y\end{array}\)
Итак,
\( \displaystyle \begin{array}{l}\Delta g=\underbrace{\left( f+\Delta f \right)}_{f\left( x+\Delta x \right)}\cdot \underbrace{\left( y+\Delta y \right)}_{y\left( x+\Delta x \right)}-f\cdot y=f\cdot y+\Delta f\cdot y+f\cdot \Delta y+\Delta f\cdot \Delta y-f\cdot y=\\=\Delta f\cdot y+f\cdot \Delta y+\Delta f\cdot \Delta y.\end{array}\)
Производная:
\( \displaystyle {g}’\underset{\text{при}\Delta x\to 0}{\mathop{=}}\,\frac{\Delta g}{\Delta x}=\frac{\Delta f\cdot y+f\cdot \Delta y+\Delta f\cdot \Delta y}{\Delta x}=\frac{\Delta f}{\Delta x}\cdot y+f\cdot \frac{\Delta y}{\Delta x}+\frac{\Delta f}{\Delta x}\cdot \Delta y\)
\( \displaystyle ={f}’y+f{y}’+{f}’\Delta y\)
Но при \( \displaystyle \Delta x\to 0\) приращение любой функции тоже бесконечно мало: \( \displaystyle \Delta y\to 0\). Поэтому последним слагаемым в выражении для производной \( \displaystyle {g}’\) можно пренебречь:
\( \displaystyle {g}’={f}’y+f{y}’\text{ }\Rightarrow \text{ }{{\left( fy \right)}^{\prime }}={f}’y+f{y}’\), ч.т.д.
Три примера на тренировку
- Докажи правило 0 с помощью правила 2;
- Найди производную выражения \( \displaystyle {{x}^{2}}\cdot \sin x\);
- Найди производную функции \( \displaystyle y=\sin 2x\).
Решения:
4. Производная частного
\( \displaystyle {{\left( \frac{f}{y} \right)}^{\prime }}=\frac{{f}’y-f{y}’}{{{y}^{2}}}\)
Здесь все аналогично: введем новую функцию \( \displaystyle g=\frac{f}{y}\) и найдем ее приращение:
\( \displaystyle \Delta g=g\left( x+\Delta x \right)-g\left( x \right)=\frac{f\left( x+\Delta x \right)}{y\left( x+\Delta x \right)}-\frac{f\left( x \right)}{y\left( x \right)}=\)
\( \displaystyle \frac{f+\Delta f}{y+\Delta y}-\frac{f}{y}=\frac{fy+\Delta fy-fy-f\Delta y}{y\left( y+\Delta y \right)}=\frac{\Delta fy-f\Delta y}{y\left( y+\Delta y \right)}\).
Производная:
\( \displaystyle {g}’\underset{\Delta x\to 0}{\mathop{=}}\,\frac{\Delta g}{\Delta x}=\frac{\frac{\Delta fy-f\Delta y}{y\left( y+\Delta y \right)}}{\Delta x}=\frac{1}{\Delta x}\cdot \frac{\Delta fy-f\Delta y}{y\left( y+\Delta y \right)}=\)
\( \displaystyle \frac{\frac{1}{\Delta x}\cdot \left( \Delta fy-f\Delta y \right)}{y\left( y+\Delta y \right)}=\frac{\frac{\Delta f}{\Delta x}\cdot y-f\cdot \frac{\Delta y}{\Delta x}}{y\left( y+\Delta y \right)}\underset{\text{т}\text{.к}\text{. }\Delta y\to 0}{\mathop{=}}\,\frac{{f}’y-f{y}’}{{{y}^{2}}}\).
Два примера на тренировку
- Найдите производные функций\( \displaystyle y=tgx\) и \( \displaystyle y=ctgx\);
- Найдите производную функции \( \displaystyle \frac{{{x}^{3}}+2x+3}{5{x} -2}\) в точке \( \displaystyle {{x}_{0}}=2\).
Решения:
5 Производная показательной функции
Теперь твоих знаний достаточно, чтобы научиться находить производную любой показательной функции, а не только экспоненты (не забыл еще, что это такое?).
Итак, \( \displaystyle f\left( x \right)={{a}^{x}}\), где \( \displaystyle a\) – это какое-то число \( \displaystyle \left( a>0,\text{ }a\ne 1 \right)\).
Мы уже знаем производную функции \( \displaystyle {{e}^{x}}\), поэтому давай попробуем привести нашу функцию \( \displaystyle {{a}^{x}}\) к новому основанию \( \displaystyle e\):
Для этого воспользуемся простым правилом: \( \displaystyle a={{e}^{\ln a}}\). Тогда:
\( \displaystyle {{a}^{x}}={{\left( {{e}^{\ln a}} \right)}^{x}}={{e}^{x\cdot \ln a}}\).
Ну вот, получилось. Теперь попробуй найти производную, и не забудь, что эта функция – сложная.
Получилось?
Вот, проверь себя:
\( \displaystyle {{\left( {{a}^{x}} \right)}^{\prime }}={{\left( {{e}^{x\cdot \ln a}} \right)}^{\prime }}={{e}^{x\cdot \ln a}}\cdot {{\left( x\cdot \ln a \right)}^{\prime }}\underset{т.к.\ \ln a\ это\ константа}{\mathop{=}}\,{{e}^{x\cdot \ln a}}\cdot \ln a={{a}^{x}}\cdot \ln a.\).
\( \displaystyle {{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\cdot \ln a\)
Формула получилась очень похожая на производную экспоненты: как было \( \displaystyle {{a}^{x}}\), так и осталось, появился только множитель \( \displaystyle na\), который является просто числом, но не переменной.
4 примера на тренировку. Найди производные функций:
- \( \displaystyle y={{5}^{x}}\)
- \( \displaystyle f\left( x \right)={{3}^{2x+1}}\)
- \( \displaystyle f\left( x \right)=\frac{{2}^{x}}{x}\)
- \( \displaystyle f\left( x \right)={x^2}\cdot{{4}^{x}}\)
Решения:
6. Производная логарифмической функции
Здесь аналогично: ты уже знаешь производную от натурального логарифма:
\( \displaystyle {{\left( \ln x \right)}^{\prime }}=\frac{1}{x}\),
Поэтому, чтобы найти произвольную от логарифма с другим основанием, например, \( \displaystyle a\):
\( \displaystyle y={{\log }_{a}}x\),
Нужно привести этот логарифм к основанию \( \displaystyle e\). А как поменять основание логарифма? Надеюсь, ты помнишь эту формулу:
\( \displaystyle {{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a}\).
Только теперь вместо \( \displaystyle {{\log }_{c}}\) будем писать \( \displaystyle ln\):
\( \displaystyle y={{\log }_{a}}x=\frac{\ln x}{\ln a}\),
В знаменателе получилась просто константа (постоянное число, без переменной \( \displaystyle \)). Производная получается очень просто:
\( \displaystyle {y}’={{\left( {{\log }_{a}}x \right)}^{\prime }}={{\left( \frac{\ln x}{\ln a} \right)}^{\prime }}=\frac{1}{\ln a}\cdot {{\left( \ln x \right)}^{\prime }}=\frac{1}{\ln a}\cdot \frac{1}{x}\)\( \displaystyle {{\left( {{\log }_{a}}x \right)}^{\prime }}=\frac{1}{x\cdot \ln a}\)
Производные показательной и логарифмической функций почти не встречаются в ЕГЭ, но не будет лишним знать их.
7. Производная сложной функции
Что такое «сложная функция»? Нет, это не логарифм, и не арктангенс. Данные функции может быть сложны для понимания (хотя, если логарифм тебе кажется сложным, прочти тему «Логарифмы» и все пройдет), но с точки зрения математики слово «сложная» не означает «трудная».
Представь себе маленький конвейер: сидят два человека и проделывают какие-то действия с какими-то предметами. Например, первый заворачивает шоколадку в обертку, а второй обвязывает ее ленточкой. Получается такой составной объект: шоколадка, обернутая и обвязанная ленточкой. Чтобы съесть шоколадку, тебе нужно проделать обратные действия в обратном порядке.
Давай создадим подобный математический конвейер: сперва будем находить косинус числа, а затем полученное число возводить в квадрат.
Итак, нам дают число \( \displaystyle x\) (шоколадка), я нахожу его косинус (обертка), а ты затем возводишь то, что у меня получилось, в квадрат (обвязываешь ленточкой). Что получилось?
Функция \( \displaystyle y={{\cos }^{2}}x\). Это и есть пример сложной функции: когда для нахождения ее значения мы проделываем первое действие непосредственно с переменной, а потом еще второе действие с тем, что получилось в результате первого.
Другими словами, сложная функция – это функция, аргументом которой является другая функция: \( \displaystyle y\left( f\left( x \right) \right)\).
Для нашего примера \( \displaystyle f\left( x \right)=\cos x\), \( \displaystyle y\left( x \right)={{x}^{2}}\).
Тогда \( \displaystyle y\left( f\left( x \right) \right)={{\left( f\left( x \right) \right)}^{2}}={{\left( \cos x \right)}^{2}}={{\cos }^{2}}x\).
Мы вполне можем проделывать те же действия и в обратном порядке: сначала ты возводишь \( \displaystyle x\) в квадрат, а я затем ищу косинус полученного числа: \( \displaystyle f=\cos \left( {{x}^{2}}\right)\). Несложно догадаться, что результат будет почти всегда разный. Важная особенность сложных функций: при изменении порядка действий функция меняется.
Второй пример: \( \displaystyle y\left( x \right)={{x}^{2}};\text{ }f\left( x \right)=\cos x\)(то же самое). \( \displaystyle f\left( y\left( x \right) \right)=\cos y\left( x \right)=\cos \left({{x}^{2}}\right)\).
Действие, которое делаем последним будем называть «внешней» функцией, а действие, совершаемое первым – соответственно «внутренней» функцией (это неформальные названия, я их употребляю только для того, чтобы объяснить материал простым языком).
Попробуй определить сам, какая функция является внешней, а какая внутренней:
Пять примеров на тренировку
- \( \displaystyle {{\sin }^{3}}x\);
- \( \displaystyle tg\sqrt{x}\)
- \( \displaystyle \sqrt{\cos x}\)
- \( \displaystyle {{\left( {{x}^{3}}+2x+1 \right)}^{5}}\)
- \( \displaystyle \sqrt[3]{2{{x}^{2}}+3}\)
Решения:
Разделение внутренней и внешней функций очень похоже на замену переменных: например, в функции
- Первым будем выполнять какое действие? Сперва посчитаем синус, а только потом возведем в куб.
Значит, внутренняя функция \( \displaystyle y\left( x \right)=\sin x\), а внешняя \( \displaystyle f\left( x \right)={{x}^{3}}\).
А исходная функция является их композицией: \( \displaystyle f\left( y\left( x \right) \right)={{y}^{3}}\left( x \right)={{\sin }^{3}}x\).
- Внутренняя: \( \displaystyle y\left( x \right)=\sqrt{x}\); внешняя:\( \displaystyle f(x)=tg\ x\).
Проверка:\( \displaystyle f(y(x))=tg(y(x))=tg\sqrt{x}\).
- Внутренняя: \( \displaystyle y\left( x \right)=\cos x\); внешняя: \( \displaystyle f\left( x \right)=\sqrt{x}\).
Проверка: \( \displaystyle f\left( y\left( x \right) \right)=\sqrt{y\left( x \right)}=\sqrt{\cos x}\).
- Внутренняя: \( \displaystyle y\left( x \right)={{x}^{3}}+2x+1\); внешняя: \( \displaystyle f\left( x \right)={{x}^{5}}\).
Проверка: \( \displaystyle f\left( y\left( x \right) \right)={{\left( y\left( x \right) \right)}^{5}}={{\left( {{x}^{3}}+2x+1 \right)}^{5}}\).
- Внутренняя: \( \displaystyle y\left( x \right)=2{{x}^{2}}+3\); внешняя: \( \displaystyle f\left( x \right)=\sqrt[3]{x}\).
Проверка: \( \displaystyle f\left( y\left( x \right) \right)=\sqrt[3]{y\left( x \right)}=\sqrt[3]{\left( 2{{x}^{2}}+3 \right)}\).
\( \displaystyle f\left( x \right)=\sqrt{\cos x}\) производим замену переменных \( \displaystyle y=\cos x\) и получаем функцию \( \displaystyle f\left( y \right)=\sqrt{y}\).
Ну что ж, теперь будем извлекать нашу шоколадку – искать производную.
Порядок действий всегда обратный: сначала ищем производную внешней функции, затем умножаем результат на производную внутренней функции.
Применительно к исходному примеру это выглядит так:
\( \displaystyle \begin{array}{l}y\left( f\left( x \right) \right)={{\cos }^{2}}x;\\f\left( x \right)=\cos x;\text{ }{f}’\left( x \right)=-\sin x\\y\left( f \right)={{f}^{2}};\text{ }{y}’\left( f \right)=2f=2\cos x\\{y}’\left( f\left( x \right) \right)={y}’\left( f \right)\cdot {f}’\left( x \right)=2\cos x\cdot \left( -\sin x \right)=-2\cos x\cdot \sin x=-\sin 2x\end{array}\)
Другой пример:
\( \displaystyle \begin{array}{l}f(x)=\sin \ (2{{x}^{2}}+1)\\\ \ \ \ \ \ \ \ \ \ \uparrow \ \ \ \ \ \ \ \ \ \uparrow \\внешняя\ \ \ \text{внутренняя}\end{array}\)
\( \displaystyle \begin{array}{l}{f}’\left( x \right)=\cos \left( 2{{x}^{2}}+1 \right)\cdot \left( 2\cdot 2x+0 \right)=4x\cdot \cos \left( 2{{x}^{2}}+1 \right)\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \uparrow \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \uparrow \ \\\ \ \ \ производная\ \ \ \ \ \ \ производная\\\ \ \ \ внешней\ \ \ \ \ \ \ \ \ \ \ \ \ \ внутренней\end{array}\).
Итак, сформулируем, наконец, официальное правило:
\( \displaystyle {{\left[ f\left( y\left( x \right) \right) \right]}^{\prime }}={f}’\left( y\left( x \right) \right)\cdot {y}’\left( x \right)\)
или проще:
\( \displaystyle {{\left[ f\left( y \right) \right]}^{\prime }}={f}’\left( y \right)\cdot {y}’\)
Алгоритм нахождения производной сложной функции:
| Алгоритм | Пример: \( \displaystyle \sqrt{\sin x}\) |
| 1. Определяем «внутреннюю» функцию, находим ее производную. | Внутренняя функция: \( \displaystyle y=\sin x\).\( \displaystyle {y}’=\cos x\) |
| 2. Определяем «внешнюю» функцию, находим ее производную. | Внешняя функция:\( \displaystyle f\left( y \right)=\sqrt{y}={{y}^{\frac{1}{2}}}\).\( \displaystyle {f}’\left( y \right)=\frac{1}{2}{{y}^{-\frac{1}{2}}}=\frac{1}{2\sqrt{y}}=\frac{1}{2\sqrt{\sin x}}\) |
| 3. Умножаем результаты первого и второго пунктов. | \( \displaystyle {f}’\left( x \right)=\frac{\cos x}{2\sqrt{\sin x}}\). |
Вроде бы всё просто, да?
Проверим на примерах:
- \( \displaystyle \sin 2x\)
- \( \displaystyle tg\ ({{x}^{2}}+2x+1)\)
- \( \displaystyle {{\left( 5{{x}^{2}}-3x+4 \right)}^{4}}\)
- \( \displaystyle \sqrt{\cos \left( 2x+3 \right)}\)
- \( \displaystyle {{\sin }^{2}}\sqrt{2x+1}\)
- \( \displaystyle y\left( x \right)=\frac{3}{{{4}^{1-3x}}}\)
- \( \displaystyle y=5\cdot {{2}^{{{x}^{2}}}}\)
Решения:
Бонусы. СЕМЬ (!) вебинаров по производной из нашего курса по подготовке к ЕГЭ
Если ты хочешь знать… ну практически все о производной, посмотри 5 вебинаров из марафона к ЕГЭ 2022 года и еще два к ЕГЭ 2021 года.
Производная в 2022 году может стоить тебе потери 4-х первичных балла на ЕГЭ (если ты ее не знаешь). Две задачи в первой части по одному баллу и экономическая задача (2 балла).
Плюс производная может попасться в задаче с параметром (а это еще 4 балла!).
Ну и в институте о производной заговорят прямо с первых лекций.
Так что имеет смысл разобраться с ней.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций»
Производная на ЕГЭ 2022. Урок 1 из 5. Геометрический смысл производной — основы
Знаете, с чего начнётся ваша учёба в универе? Я имею в виду не общагу, а первые лекции по математике.
С производной (ну, почти сразу).
Но чтобы в этот самый универ поступить, нужно сдать ЕГЭ, в котором, оказывается, тоже есть производная. И если мы уже привыкли, что в первой части есть две задачи на неё, то во второй мы её не ожидаем увидеть.
Но она там частенько бывает нужна: в экономической задаче №16 (бывшая 17). А иногда и в 18 на параметр (бывшая 19). Поэтому, плохо зная производную, вы рискуете лишиться 4 первичных баллов!
На этом курсе я вам очень просто и понятно расскажу, что такое производная, и вы научитесь решать задачи из ЕГЭ без ошибок!
Производная на ЕГЭ 2022. Урок 2 из 5. Более сложные задачи
На прошлом уроке мы познакомились с производной, узнали, что это такое, в чём её смысл и где она применяется.
А также мы научились решать один из самых распространённых типов задач № 6 из профильного ЕГЭ (бывший №7).
Теперь мы возьмёмся за более сложные типы задач, и увидим, что если мы поняли, что такое производная и в чём её «геометрический смысл» (если ещё не знаете – посмотрите первый урок), то любая задача №6 нам по зубам.
Производная на ЕГЭ 2022. Урок 3 из 5. Формулы производных и правила дифференцирования
Геометрический (а также физический) смысл производной мы с вами уже поняли, задачу №6 научились решать вдоль и поперёк. В основном это задачи с рисунками: по рандомному графику нужно определить, где функция возрастает, а где убывает.
Теперь же пришло время рассмотреть конкретные функции (заданные формулой, а не графиком) и научиться находить их производные.
Мы с вами выучим формулы производных всех элементарных функций, а также все базовые правила дифференцирования. Это поможет нам научиться решать половину всех задач №11 (бывшая №12) из профиля.
Более того, вы узнаете, откуда все эти правила и формулы появились! Мало в какой школе это объясняют на уроках математики. Но это помогает очень хорошо понять и «почувствовать» производную, чтобы она уже никогда не казалась чем-то сложным и пугающим.
Производная на ЕГЭ 2022. Урок 4 из 5. Производная сложной функции
А теперь пришло время производной сложной функции. Что такое сложная функция? Как искать её производную? Почему именно так и откуда берутся эти правила?
Если хотите услышать простые ответы на вопросы о сложных функциях – смотрите это видео.
Производная на ЕГЭ 2022. Урок 5 из 5. Задача на оптимизацию с применением производной
Окей, вот мы и натренировались искать производные данных нам функций, понимаем, что это такое и как с их помощью находить минимумы и максимумы.
Но зачем?
Банальный ответ «чтобы решать задачи №6 и 11» звучит довольно глупо, если вспомнить, сколько я распрягал про смысл и понимание производной. Можно было бы просто зазубрить пару формул, запомнить схему решения задач и благополучно забыть их, выйдя с экзамена.
Но оказывается, что производная бывает нужна ещё и в других задачах, например – в экономической №15 (бывшая 17). А без понимания производной будет просто нереально догадаться, что её нужно в этой задаче применять!
Как не лишиться 2 первичных баллов – смотрите в этом видео на примере задачи №15 на оптимизацию.
ЕГЭ №6 (бывшая №7) Производная функции — геометрический смысл, дифференцирование (ЕГЭ — 2021)
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
Экономическая задача на производную (ЕГЭ №15, бывшая 17-я задача)
В 2017 году, придя на экзамен, выпускники облегченно выдохнули: они увидели под 17 номером стандартную задачу на кредиты. Они боялись, что им попадется такая же задача, как на пробном ЕГЭ.
Задача-убийца, которая была чуть ли не сложнее, чем 18 и 19 вместе взятые. Кстати, те, кто сдавал в резервный день, халявы уже не получили, им тоже досталась сложная задача.
На ЕГЭ можно ожидать чего угодно, поэтому готовьтесь с нами к самым сложным задачам. Смотрите это видео и вы научитесь решать самую сложную задачу на оптимизацию и подобные ей.
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



все стало намного понятнее, спасибо
Спасибо, очень помогло в освоении производной!
Отлично, Валентина. Тема простая, если знать как ее подать )
спасибо большое
Пожалуйста, Константин.
Крутая аналогия про дорогу! Прямо как мои оценки до того, как я нашла этот сайт! Теперь понимаю математику, может вскоре и физику начну))
Юный физик, спасибо! Ты очень крута, раз сумела разобраться в такой сложной теме! Мы как раз готовим статьи по физике! Будешь настоящим физиком-ядерщиком! (или «ядриком-физерщиком» ;)) З.Ы. Привет от Александра 🙂
Очень хорошая статья! Все четко и понятно, помогла разобраться с заданием. Спасибо!
Виктория, спасибо! Заходите, читайте другие статьи, пишите нам, если понравится и не только если понравится. ЗЫ. Привет от Саши, кстати. ))
Некоторые комментарии к этой статье за прошлые годы:
Сергей
15 февраля 2018
Спасибо, помогли повторить основы дифференцирования.
Никита
20 июня 2018
Отличное объяснение. Спасибон.
Виктория
01 января 2019
Все объяснено предельно просто и понятно. Огромное спасибо за Ваши труды!
Ирина
25 апреля 2019
Спасибо за простоту и доходчивость. Решила помочь сыну подтянуть материал и по его лекциям не разобралась в теме, но когда прочла ваш материал, то сразу все легло по полочкам. Занимаюсь теперь с сыном. Спасибо.
Раха
02 августа 2019
Спасибо большое очень хороший сайт вы создали
Глеб Рождественский
01 декабря 2019
Круто, разобрался с нахождением производной по определению и производной сложной функции. Спасибо, хороший материал , лайк!
Билолиддин
09 апреля 2020
Спасибо вам за такой труд! Вы классно объяснили всю эту крутизну)
Владимир
14 июля 2020
Просто, доходчиво, увлекательно. Спасибо. Помогу дочери разобраться в этой теме.