Формулы тригонометрии
В этой статье мы изучим все тригонометрические формулы, которые могут понадобится на ЕГЭ.
От основного тригонометрического тождества, до формул тройного угла.
Мы решим вместе 22 примера, чтобы «набить руку» и уметь решать любые задачи.
Поехали!
Формулы тригонометрии — коротко о главном
Основные формулы:
| Название формулы | Формула |
|---|---|
| Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!) | \( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\) |
| Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса) | \( \displaystyle tg\ \alpha =\frac{sin\ \alpha }{cos\ \alpha }\) |
| Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса) | \( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }=\frac{1}{tg\ \alpha }\) |
| Синус суммы и разности: | \( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \) |
| Косинус суммы и разности: | \( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \) |
| Тангенс суммы и разности: | \( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\) |
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
- \( \displaystyle si{{n}^{2}}\alpha =\frac{1-cos2\alpha }{2}\)
- \( \displaystyle co{{s}^{2}}\alpha =\frac{1+cos2\alpha }{2}\)
- \( \displaystyle si{{n}^{3}}\alpha =\frac{3sin\alpha -sin3\alpha }{4}\)
- \( \displaystyle co{{s}^{3}}a=\frac{3cosa+cos3a}{4}\)
- \( \displaystyle t{{g}^{2}}\alpha =\frac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \frac{\pi }{2}+\pi n,n\in Z\)
Формулы преобразования функций:
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
- \( \displaystyle sin\alpha \pm sin\beta =2sin\frac{\alpha \pm \beta }{2}cos\frac{\alpha \mp \beta }{2}\)
- \( \displaystyle cos\alpha +cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}\)
- \( \displaystyle cos\alpha -cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}\)
- \( \displaystyle tg\alpha \pm tg\beta =\frac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta }\)
- \( \displaystyle ctg\alpha \pm ctg\beta =\frac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta }\)
Формулы преобразования произведений функций:
- \( \displaystyle sin\alpha sin\beta =\frac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2}\)
- \( \displaystyle sin\alpha cos\beta =\frac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2}\)
- \( \displaystyle cos\alpha cos\beta =\frac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2}\)
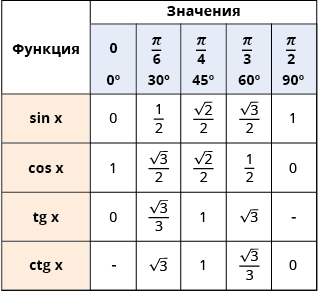
Таблица значений тригонометрических функций:
Тригонометрические функции
Как ты уже понял, тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций.
Стоп! Вот прямо здесь мы и остановимся! Я задам тебе вопрос: какие тригонометрические функции ты знаешь?
Верно! Их всего четыре!
- Синус \( \displaystyle sin\left( x \right)\)
- Косинус \( \displaystyle cos\left( x \right)\)
- Тангенс \( \displaystyle tg\left( x \right)\)
- Котангенс \( \displaystyle ctg\left( x \right)\)
Хотя, положа руку на сердце, я скажу тебе, что знание последней не так уж и обязательно (хотя желательно!), поскольку она легко выражается через тангенс.
Да и сам тангенс, по сути – тоже лишь тригонометрическое выражение, зависящее от синуса и косинуса.
Таким образом, у нас есть две основные тригонометрические функции – синус и косинус и две «второстепенные» – тангенс и котангенс.
Я не буду сейчас определять, что такое синус и косинус, ты и так это уже знаешь из предыдущих разделов. Я лишь скажу пару слов про важность этих понятий.
Итак, пара слов: первые зачатки тригонометрии возникли более 3 тысяч лет назад. Я думаю, что тебе очевидно, что тогда люди не занимались «формулами ради формул».
Так что тригонометрические функции имеют полезные практические свойства. Я не буду их перечислять. Если тебе интересно, ты всегда можешь найти море информации в интернете.
Если все, что я сказал выше, звучало для тебя древним эльфийским языком, то посмотри статью о тригонометрической окружности.
А сейчас я приведу тебе некоторые основные соотношения между тригонометрическими величинами, которые оказываются полезными при решении задач.
Таблица значений тригонометрических функций
Тебе нужно помнить таблицу значений тригонометрических функций для углов хотя бы первой четверти! Я сейчас нарисую здесь эту таблицу, а потом объясню тебе, как сделать ее запоминание проще.

Или ее расширенный вариант для всех «основных углов»:
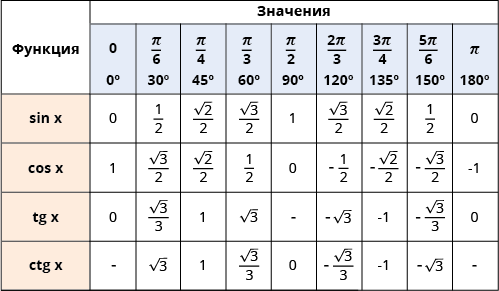
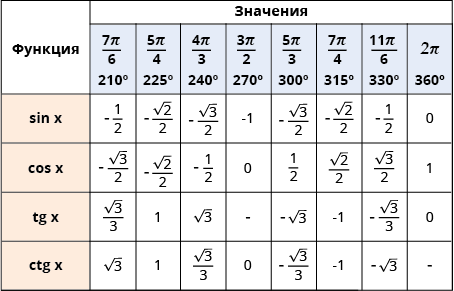
Я ни в коей мере не настаиваю (и даже не надеюсь), что ты выучишь вторую таблицу. Сказать по правде, я и сам ее не знаю.
Но первую таблицу знать совершенно необходимо.
Не всегда на экзамене у тебя будет время, чтобы вывести самостоятельно, скажем, синус \( \displaystyle 60\) градусов.
Для того, чтобы запомнить первую таблицу можно поступить так:
Запомнить всего 5 значений для, скажем, синуса. Затем тебе не составит труда заметить, что для косинуса все значения идут «наоборот»:
- Например, синус \( \displaystyle 0\) градусов равен нулю значит, косинус \( \displaystyle 0\) градусов – наоборот: единица.
- Синус \( \displaystyle 90\) градусов равен единице, значит косинус \( \displaystyle 90\) градусов равен нулю.
- Синус \( \displaystyle 30\) градусов равен \( \displaystyle \frac{1}{2}\), значит косинус \( \displaystyle 30\) градусов равен \( \displaystyle \frac{\sqrt{3}}{2}\) и т. д.
Тангенс можно получить, разделив синус угла на косинус. Как же всегда вывести большую таблицу, зная малую, я тебе непременно расскажу чуть позднее.
Формулы тригонометрии (основа)
| Название формулы | Формула |
|---|---|
| Основное тригонометрическое тождество (ночью разбудят — должен вспомнить!) | \( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\) |
| Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса) | \( \displaystyle tg\ \alpha =\frac{sin\ \alpha }{cos\ \alpha }\) |
| Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса) | \( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }=\frac{1}{tg\ \alpha }\) |
| Первое следствие формулы 1: | \( \displaystyle t{{g}^{2}}\alpha +1=\frac{1}{co{{s}^{2}}\alpha }\) |
| Второе следствие формулы 1: | \( \displaystyle ct{{g}^{2}}\alpha +1=\frac{1}{si{{n}^{2}}\alpha }\) |
| Третье следствие формулы 1: | \( \displaystyle sin\ \alpha =\pm \sqrt{1-co{{s}^{2}}\alpha }\) |
| Четвертое следствие формулы 1: | \( \displaystyle cos\ \alpha =\pm \sqrt{1-si{{n}^{2}}\alpha }\) |
Уже получилось 7 формул! К сожалению, это еще далеко не предел. Совсем не предел.
Тем не менее последние 4 формулы есть ни что иное, как простое следствие первой. В самом деле, ты заметил, почему это так?
Формула 4 получается делением обеих частей формулы 1 на \( \displaystyle co{{s}^{2}}\alpha \) и применением формулы 2.
Формула 5 получается аналогично: разделим обе части формулы 1 на \( \displaystyle si{{n}^{2}}\alpha \) и вместо выражения \( \displaystyle \frac{co{{s}^{2}}\alpha }{si{{n}^{2}}\alpha }\) запишем \( \displaystyle ct{{g}^{2}}\alpha \), исходя из определения 3.
Формулы 1 – 5 мы трактуем вполне однозначно. Чего нельзя сказать про формулы 6 и 7. В чем «фишка» формул 6 и 7?
Их особенность заключается в знаке \( \displaystyle \pm \), который стоит перед корнем.
Как это понимать? А понимать надо так: в некоторых случаях мы ставим плюс, а в некоторых – минус.
Теперь у тебя должен возникнуть вопрос: в каких-таких «некоторых случаях»? Туманность этой формулировки снимается следующим правилом:
Если в формуле
\( \displaystyle sin\ \alpha =\pm \sqrt{1-co{{s}^{2}}\alpha }\)
угол \( \displaystyle \alpha \) таков, что \( \displaystyle \text{sin}\ \text{ }\!\!\alpha\!\!\text{ }<0\), то ставим знак «минус», иначе – «плюс».
Если в формуле
\( \displaystyle cos\ \alpha =\pm \sqrt{1-si{{n}^{2}}\alpha }\)
угол \( \displaystyle \alpha \) таков, что \( \displaystyle \text{cos}\ \text{ }\!\!\alpha\!\!\text{ }<0\), то ставим знак «минус», иначе – «плюс».
Есть опять некий «запутанный» момент в правиле, не так ли? В чем осталось разобраться?
Осталось понять, как связан угол со знаком тригонометрической функции. Ответом на этот вопрос (если ты, конечно, забыл) служат следующие картинки:
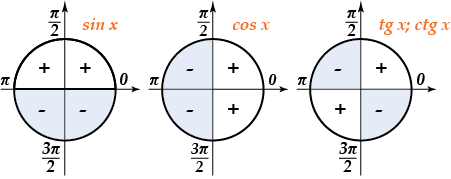
Они подскажут тебе, какой нужно выбирать знак для той или иной функции, так что ты не допустишь досадной ошибки.
К тому же это избавит тебя от мучительных размышлений по поводу того «а зачем в этом примере нужен этот угол?!».
4 примера на тренировку
- Найдите \( \displaystyle \text{3cos}\ \text{ }\!\!\alpha\!\!\text{ }\), если \( \displaystyle sin\alpha =-\frac{2\sqrt{2}}{3}\) и \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\).
- Найдите \( \displaystyle 5\sin\alpha\), если \( \displaystyle cos\alpha =\frac{2\sqrt{6}}{5}\) и \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\).
- Найдите \( \displaystyle \text{cos}\ \text{ }\!\!\alpha\!\!\text{ }\) если \( \displaystyle sin\alpha =\frac{2\sqrt{6}}{5}\) и \( \displaystyle \alpha \in \left( \frac{\pi }{2};\pi \right)\).
- Найдите \( \displaystyle \text{tg}\ \text{ }\!\!\alpha\!\!\text{ }\), если \( \displaystyle sin\alpha =-\frac{5}{\sqrt{26}}\) и \( \displaystyle \alpha \in \left( \pi ;\frac{3\pi }{2} \right)\).
Решения:
1. Так как \( \displaystyle cos\alpha =\pm \sqrt{1-si{{n}^{2}}\alpha }\), то подставим сюда значение\( \displaystyle sin\alpha =-\frac{2\sqrt{2}}{3}\), тогда \( \displaystyle cos\alpha =\pm \sqrt{1-{{\left( -\frac{2\sqrt{2}}{3} \right)}^{2}}}=\pm \sqrt{1-\frac{4\cdot 2}{9}}=\pm \sqrt{1-\frac{8}{9}}=\)
\( \displaystyle=\pm \sqrt{\frac{1}{9}}=\pm \frac{1}{3}.\)Теперь дело за малым: разобраться со знаком. Что нам для этого нужно? Знать, в какой четверти находится наш угол.
По условию задачи: \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\). Смотри на картинку. Какая это четверть? Четвертая.
Каков знак косинуса в четвертой четверти? На картинке стоит знак «плюс», значит косинус в четвертой четверти положительный.
Тогда нам остается выбрать знак «плюс» перед \( \displaystyle \frac{1}{3}\). \( \displaystyle \text{cos}\ \text{ }\!\!\alpha\!\!\text{ }=\frac{1}{3}\), тогда \( \displaystyle 3cos\alpha =3\cdot \frac{1}{3}=1\).
Ответ: \( \displaystyle 1\).
Ну вот видишь, ничего сложного. Абсолютно ничего. Нужно лишь запомнить знаки синуса, косинуса и тангенса (котангенса) по четвертям. Ну а как это делать автоматически описано в статье, посвященной тригонометрической окружности.
Давай разберем оставшиеся примеры.
2. Так как \( \displaystyle sin\ \alpha =\pm \sqrt{1-co{{s}^{2}}\alpha }\), то все, что нам нужно – это подставить \( \displaystyle cos\alpha =\frac{2\sqrt{6}}{5}\) в нашу формулу. Что мы с тобой и сделаем:
\( \displaystyle sin\alpha =\pm \sqrt{1-{{\left( \frac{2\sqrt{6}}{5} \right)}^{2}}}=\pm \sqrt{1-\left( \frac{4\cdot 6}{25} \right)}=\pm \sqrt{\frac{1}{25}}=\pm \frac{1}{5}\).
Опять нужно определиться со знаком. Смотрим на рисунок. Четверть – снова четвертая. Знак синуса четвертой четверти – отрицательный. Ставим знак «минус». \( \displaystyle sin\alpha =-\frac{1}{5}\), тогда \( \displaystyle 5sin\alpha =-5\cdot \frac{1}{5}=-1\).
Ответ: \( \displaystyle -1\).
3. Ничего нового. Скорее для закрепления. Снова подставляем в формулу \( \displaystyle cos\ \alpha =\pm \sqrt{1-si{{n}^{2}}\alpha }\) значение \( \displaystyle sin\alpha =\frac{2\sqrt{6}}{5}\):
\( \displaystyle cos\alpha =\pm \sqrt{1-{{\left( \frac{2\sqrt{6}}{5} \right)}^{2}}}=\pm \sqrt{1-\left( \frac{4\cdot 6}{25} \right)}=\pm \sqrt{\frac{1}{25}}=\pm \frac{1}{5}\).
Смотрим на знак косинуса при \( \displaystyle \alpha \in \left( \frac{\pi }{2};\pi \right)\). Какая это четверть? Вторая. Косинус второй четверти отрицательный. Тогда выбираем знак «минус».
Ответ: \( \displaystyle -0,2\).
4. Здесь перед нами стоит задачка чуть сложнее. Однако, не стоит огорчаться. Давай вспомним, что такое тангенс. Это ведь отношение синуса к косинусу. Синус нам уже дан.
Давай вначале найдем косинус. Как это сделать, ты уже знаешь. \( \displaystyle cos\alpha =\pm \sqrt{1-{{\left( -\frac{5}{\sqrt{26}} \right)}^{2}}}=\pm \sqrt{1-\frac{25}{26}}=\pm \sqrt{\frac{1}{26}}=\pm \frac{1}{\sqrt{26}}\).
Так как \( \displaystyle \alpha \in \left( \pi ;\frac{3\pi }{2} \right)\) (это угол в третьей четверти, а косинус в третьей четверти имеет знак «минус»), то \( \displaystyle cos\alpha =-\frac{1}{\sqrt{26}}\).
Теперь все, что нам осталось, это воспользоваться определением тангенса:
\( \displaystyle tg\alpha =\frac{sin\alpha }{cos\alpha }=\frac{-\frac{5}{\sqrt{26}}}{-\frac{1}{\sqrt{26}}}=5.\)Ответ: \( \displaystyle 5\).
Уф, выдохнули! Ну вот мы с тобой решили некоторые (довольно типичные и распространенные) примеры. Ты спросишь: «И что, это все?». Я отвечу, что, увы нет. Это далеко не все.
Далее нам потребуются более сложные формулы тригонометрии.
Формулы тригонометрии (более сложные)
| Название формулы | Формула |
|---|---|
| Синус суммы и разности: | \( \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \) |
| Косинус суммы и разности: | \( \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \) |
| Тангенс суммы и разности: | \( \displaystyle tg\left( \alpha \pm \beta \right)=\frac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta }\) |
| Синус двойного угла (следствие формулы 1) | \( \displaystyle sin2a=2sina\cdot cosa\) |
| Косинус двойного угла (следствие формулы 2) | \( \displaystyle cos2a=co{{s}^{2}}a-si{{n}^{2}}a\) \( \displaystyle cos2a=2co{{s}^{2}}a-1=1-2si{{n}^{2}}a\) |
| Тангенс двойного угла: | \( \displaystyle tg2a=\frac{2tga}{1-t{{g}^{2}}a}\) |
Как распознать, что тебе требуются именно эти, а не какие-нибудь другие формулы?
Очень просто: если ты видишь косинус, синус, тангенс от суммы двух углов или двойных углов, то это должно служить тебе индикатором – мне нужно применить одну из формул для суммы/разности или для двойного угла.
Звучит несколько путано? Давай посмотрим на примеры. Заодно я дам еще ряд важных комментариев.
9 примеров на тренировку
- \( \displaystyle \frac{12sin11{}^\circ cos11{}^\circ }{sin22{}^\circ }\)
- \( \displaystyle \frac{24\left( si{{n}^{2}}17{}^\circ -co{{s}^{2}}17{}^\circ \right)}{cos34{}^\circ }\)
- \( \displaystyle 36\sqrt{6} ctg \frac{\pi}{6} \sin \frac{\pi }{4}\)
- Найдите \( \displaystyle -47cos2a\), если \( \displaystyle cosa=-0,4\)
- Найдите \( \displaystyle \frac{10sin6a}{3cos3a}\), если \( \displaystyle sin3a=0,6\)
- Найдите \( \displaystyle 26\text{cos}\left( \frac{3\pi }{2}+a \right)\), если \( \displaystyle cosa=\frac{12}{13}\) и \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\)
- Найдите \( \displaystyle t{{g}^{2}}a\), если \( \displaystyle 5si{{n}^{2}}a+13co{{s}^{2}}a=6\)
- Найдите \( \displaystyle \frac{10cosa+4sina+15}{2sina+5cosa+3}\), если \( \displaystyle tga=-2,5\)
- Найдите \( \displaystyle 7\cos \left( \pi +\beta \right)-2\text{sin}\left( \frac{\pi }{2}+\beta \right)\), если \( \displaystyle cos\beta =-\frac{1}{3}\)
Список этих заданий можно продолжать бесконечно… Но я выбрал здесь: а) не самые сложные формулы; б) не самые «страшные» углы.
Страшные углы я припас нам напоследок 🙂
Решения:
Кстати, здесь тебе понадобится знание также тех формул, которые я привел в самом начале. Поехали!
1. \( \displaystyle \frac{12sin11{}^\circ cos11{}^\circ }{sin22{}^\circ }\)
Ни ты, ни я не знаем, чему в точности равен синус или косинус \( \displaystyle 11\) градусов, и чему равен синус \( \displaystyle 22\) градусов.
Но что мы должны заметить?
Верно! \( \displaystyle 22{}^\circ =2\cdot 11{}^\circ \). Значит, снизу записан синус двойного угла! Тогда применим формулу синуса двойного угла:
\( \displaystyle sin22{}^\circ =2sin11{}^\circ \cdot cos11{}^\circ \)Подставим это значение в знаменатель нашей дроби и сократим!
\( \displaystyle \frac{12sin11{}^\circ \cdot cos11{}^\circ }{sin22{}^\circ }=\frac{12sin11{}^\circ \cdot cos11{}^\circ }{2sin11{}^\circ \cdot cos11{}^\circ }=6\).
Ответ: \( \displaystyle 6\).
Ну вот, ничего страшного не случилось? Пример решился в одну строчку с применением одной единственной формулы. Другое дело, иногда не совсем очевидно, какую из формул применять.
Тут тебе нужен опыт. Нужно, как говорится, «набить руку» на таких примерах.
2. \( \displaystyle \frac{24\left( si{{n}^{2}}17{}^\circ -co{{s}^{2}}17{}^\circ \right)}{cos34{}^\circ }\)
Опять-таки, сразу можно заметить, что \( \displaystyle 34{}^\circ =2\cdot 17{}^\circ \). \( \displaystyle 34\) градуса стоит в косинусе. Это говорит о том, что в примере спрятан косинус двойного угла. Вспомним его определение:
\( \displaystyle cos2a=co{{s}^{2}}a-si{{n}^{2}}a\)Что же у нас есть в числителе? А там все наоборот: синус в квадрате вычитается из косинуса в квадрате. Тогда в числителе у нас написана формула чего?
3. \( \displaystyle 36\sqrt{6}ctg\frac{\pi }{6}\sin\frac{\pi }{4}\)
Здесь нет ничего сложного, абсолютно ничего! Но есть одно «но!».
Это «но» заключается в том, что тебе нужно помнить таблицу значений тригонометрических функций для углов хотя бы первой четверти! (Как ее запомнить я рассказал ранее, а сейчас просто приведу ее еще раз).

Или ее расширенный вариант для всех «основных углов»:


И посмотрим в таблицу:
\( \displaystyle ctg\frac{\pi }{6}=\sqrt{3}\), \( \displaystyle sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}\). Подставим эти значения в нашу формулу:
\( \displaystyle 36\sqrt{6} ctg\frac{\pi }{6}sin\frac{\pi }{4}=36\sqrt{6}\cdot \sqrt{3}\cdot \frac{\sqrt{2}}{2}=\frac{36\cdot \sqrt{6}\cdot \sqrt{6}}{2}=\frac{36\cdot 6}{2}=36\cdot 3=108\).
Ответ: \( \displaystyle 108\)
Вот видишь, знание первой таблицы совершенно необходимо! Без нее – вообще нет никакой тригонометрии. Так что, пожалуйста, будь добр, выучи.
Это не потребует от тебя значительных усилий и избавит от массы глупых ошибок в будущем. Еще раз специально скажу: большую таблицу учить не надо!!!
4. По условию \(cosa=-0,4\), нам же надо найти \(-47cos2a\).
Что тогда надо сделать?
Верно, наша цель – выразить косинус двойного угла через угол «одинарный». Есть ли такая формула? Конечно, есть! Вот она:
5. \( \displaystyle \frac{10sin6a}{3cos3a}\) – это то, что надо вычислить, а \( \displaystyle sin3a=0,6\) – это то, что есть.
Ну что же, надо отталкиваться от того, что есть. Вроде бы этого должно быть достаточно. Здесь все опять несложно!
Нужно лишь заметить, что \( \displaystyle sin6\alpha =2sin3\alpha \cdot cos3\alpha \). Давай это и подставим в числитель исходной дроби. Что же мы имеем?
6. \( \displaystyle 26\text{cos}\left( \frac{3\pi }{2}+a \right)\) – то, что нужно найти, а \( \displaystyle cosa=\frac{12}{13}\) и \( \displaystyle \alpha \in \left( \frac{3\pi }{2};2\pi \right)\) – то, что мы имеем.
На самом деле здесь можно поступать двояко. Но о втором способе я скажу тебе чуть позже. А пока давай подумаем, что нужно найти.
А найти нужно по сути косинус от суммы двух углов. Причем один из них известен. Давай не будем долго думать и разложим косинус суммы на произведение:
\( \displaystyle \cos \left( \frac{3\pi }{2}+\alpha \right)=cos\frac{3\pi }{2}cos\alpha -sin\frac{3\pi }{2}sin\alpha \)Вспомни единичную окружность (ну или на худой конец посмотри в расширенную таблицу).
Косинус углов: \( \displaystyle \frac{\pi }{2}=90{}^\circ ,~\frac{3\pi }{2}=270{}^\circ \) равен нулю!
Тогда…
7. Нужно найти: \( \displaystyle t{{g}^{2}}a\), а дано: \( \displaystyle 5si{{n}^{2}}a+13co{{s}^{2}}a=6\).
Тут все можно сделать только зная, что такое тангенс и основное тригонометрическое тождество. По порядку:
\( \displaystyle t{{g}^{2}}\alpha =\frac{si{{n}^{2}}\alpha }{co{{s}^{2}}\alpha }\),
\( \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1\)
Тогда решить задачу можно вот как: найти по отдельности значения синуса в квадрате и косинуса в квадрате, а затем при помощи полученных значений найти тангенс. Так мы с тобой и сделаем:
Вначале найдем синус в квадрате.
8. Надо найти \( \displaystyle \frac{10cosa+4sina+15}{2sina+5cosa+3}\), зная, что \( \displaystyle tga=-2,5\).
На какую мысль тебя это должно было натолкнуть?
А на ту, что если нам дан тангенс, то и наше выражение нужно привести к такому виду, чтобы оно зависело от тангенсов, которые мы потом в него и подставим. Напомню тебе, что
\( \displaystyle tg\alpha =\frac{sin\alpha }{cos\alpha }\)У меня же в выражении есть просто косинусы и синусы. Что нам нужно сделать?
Давай возьмем и «насильно» разделим числитель и знаменатель дроби на \( \displaystyle cos\alpha \). Это поможет мне «выделить» тангенс в чистом виде:
\( \displaystyle \frac{10cos\alpha +4sin\alpha +15}{2sin\alpha +5cos\alpha +3}=\frac{\frac{10cos\alpha +4sin\alpha +15}{cos\alpha }}{\frac{2sin\alpha +5cos\alpha +3}{cos\alpha }}=\frac{10+4tg\alpha +\frac{15}{cos\alpha }}{2tg\alpha +5+\frac{3}{cos\alpha }}\).
Конечно, есть одна неприятность: у нас появились дроби с косинусами. Но есть надежда, что мы с ними справимся! А пока что давай подставим вместо \( \displaystyle tga\) его числовое значение \( \displaystyle -2,5\). Тогда получим:
9. Нужно найти \( \displaystyle 7\cos \left( \pi +\beta \right)-2\text{sin}\left( \frac{\pi }{2}+\beta \right)\), если дано \( \displaystyle cos\beta =-\frac{1}{3}\).
Давай опять проанализируем, что нам нужно вычислить: искомая формула состоит из разности косинуса от суммы двух углов и синуса от суммы двух углов.
Давай упрощать: раскроем каждую из сумм (опять-таки повторюсь, что далее я опишу способ, который позволит обходиться без раскрытия такого рода сумм):
\( \displaystyle \cos \left( \pi +\beta \right)=cos\pi \cdot cos\beta -sin\pi \cdot sin\beta \)Опять-таки, тебе должно быть известно, что \( \displaystyle cos\pi =-1,~~sin\pi =0\).
Если тебе это неизвестно, то настоятельно рекомендую тебе повторить тему тригонометрическая окружность.
Тогда моя формула примет вид:
\( \displaystyle \cos \left( \pi +\beta \right)=-cos\beta =-\left( -\frac{1}{3} \right)=\frac{1}{3}\)Теперь с синусом:
Формулы приведения
Теперь мы знаем уже почти что все. Осталось совсем немного. Последнее, на что я хочу обратить внимание, это обещанный мною метод «легкого» перехода от большой таблицы значений углов к маленькой.
Этот переход обеспечивают так называемые формулы приведения. Еще раз поясню, зачем они используются: ты будешь их применять в том случае, когда тебе нужно найти синус, косинус или тангенс угла, большего чем \( \displaystyle 90\) градусов.
Например, найти синус угла \( \displaystyle 855\) градусов.
Здесь мы поступаем следующим образом. Во-первых, нам понадобятся следующие знания:
| Синус и косинус имеют период \( \displaystyle 2\pi \) (\( \displaystyle 360\) градусов), то есть | \( \displaystyle sin\left( 2\pi k+x \right)=sinx\) \( \displaystyle cos\left( 2\pi k+x \right)=cosx\) |
| Тангенс (котангенс) имеют период \( \displaystyle \pi \) (\( \displaystyle 180\) градусов) | \( \displaystyle tg\left( \pi k+x \right)=tgx\) \( \displaystyle ctg\left( \pi k+x \right)=ctgx\) \( \displaystyle k\) – любое целое число |
| Синус и тангенс – функции нечетные, а косинус – четная: | \( \displaystyle sin\left( -x \right)=-sinx\) \( \displaystyle tg\left( -x \right)=-tg\left( x \right)\) \( \displaystyle cos\left( -x \right)=cos\left( x \right)\) |
Алгоритм использования формул приведения
Шаг 1. Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул (2).
Например:
\( \displaystyle sin\left( -855{}^\circ \right)=-sin855{}^\circ ,~cos\left( -855{}^\circ \right)=cos855{}^\circ \)
Шаг 2. Отбрасываем для синуса и косинуса его периоды: \( \displaystyle 2\pi k\) (по \( \displaystyle 360\) градусов), а для тангенса – «половинки» \( \displaystyle \pi k\) (\( \displaystyle 180\) градусов).
Например:
\( \displaystyle sin\ 855{}^\circ =sin\left( 2\cdot 360{}^\circ +135{}^\circ \right)=sin\ 135{}^\circ \)
\( \displaystyle tg\ 225{}^\circ =tg\left( 180{}^\circ +45{}^\circ \right)=tg\ 45{}^\circ \)
Шаг 3. Если оставшийся «уголок» меньше \( \displaystyle 90\) градусов, то задача решена: ищем его в «малой таблице»
Шаг 4. Иначе ищем, в какой четверти лежит наш угол \( \displaystyle \alpha \): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Шаг 5. Представляем угол \( \displaystyle \alpha \) в одной из следующих форм:
- \( \displaystyle \alpha =90+\beta \) (если во второй четверти),
- \( \displaystyle \alpha =180-\beta \) (если во второй четверти),
- \( \displaystyle \alpha =180+\beta \) (если в третьей четверти),
- \( \displaystyle \alpha =270-\beta \) (если в третьей четверти),
- \( \displaystyle \alpha =270+\beta \) (если в четвертой четверти),
- \( \displaystyle \alpha =360-\beta \) (если в четвертой четверти).
…так, чтобы оставшийся угол \( \displaystyle \beta \) был больше нуля и меньше \( \displaystyle 90\) градусов.
Например: \( \displaystyle 135{}^\circ =180{}^\circ -45{}^\circ \)
\( \displaystyle 135{}^\circ =90{}^\circ +45{}^\circ \)
\( \displaystyle 315{}^\circ =270{}^\circ+45{}^\circ \)
\( \displaystyle 240{}^\circ =180{}^\circ +60{}^\circ \)
\( \displaystyle 240{}^\circ =270{}^\circ -30{}^\circ \)…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Шаг 6. Теперь смотрим, что у нас получилось:
- если ты выбрал запись через \( \displaystyle 180\) или \( \displaystyle 360\) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь \( \displaystyle 180\) или \( \displaystyle 360\) и записываешь синус, косинус или тангенс оставшегося угла.
- eсли же ты выбрал запись через \( \displaystyle 90\) или \( \displaystyle 270\) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Шаг 7. Ставим перед получившимся выражением знак из пункта 4.
3 примера на тренировку
- Вычислить \( \displaystyle sin\ 2130{}^\circ \)
- Вычислить \( \displaystyle \sqrt{2}cos\frac{21\pi }{4}\)
- Найдите значение выражения: \( \displaystyle 12\sin 150{}^\circ \cos 120{}^\circ \)
Решения:
1. \( \displaystyle sin\ 2130{}^\circ \)
Действуем согласно нашему алгоритму. Выделяем целое число кругов для \( \displaystyle 2130{}^\circ \):
\( \displaystyle \frac{2130{}^\circ }{360{}^\circ }=5,91\ldots \)
В общем, делаем вывод, что в угол \( \displaystyle 2130{}^\circ \) помещается целиком 5 раз по \( \displaystyle 360{}^\circ \), а сколько осталось? Осталось \( \displaystyle 2130{}^\circ -5\cdot 360{}^\circ =330{}^\circ \). Тогда:
\( \displaystyle sin~\ 2130{}^\circ =sin\left( 5\cdot 360{}^\circ +330{}^\circ \right)=sin\ 330{}^\circ \)
Ну вот, лишнее мы отбросили. Теперь разбираемся со знаком.
\( \displaystyle 330{}^\circ \) лежит в 4 четверти. Синус четвертой четверти имеет знак «минус», его я и не должен забыть поставить в ответе. Далее, представляем \( \displaystyle 330{}^\circ \) согласно одной из двух формул пункта 5 правил приведения. Я выберу: \( \displaystyle 330{}^\circ =270{}^\circ +60{}^\circ \)
\( \displaystyle sin\ 330{}^\circ =sin\left( 270{}^\circ +60{}^\circ \right)\)
Теперь смотрим, что получилось: у нас случай с \( \displaystyle 270\) градусами, тогда отбрасываем \( \displaystyle 270{}^\circ \) и синус меняем на косинус. И ставим перед ним знак «минус»!
\( \displaystyle sin\left( 270{}^\circ +60{}^\circ \right)=-cos60{}^\circ \)
\( \displaystyle 60\) градусов – угол в первой четверти. Мы знаем (ты мне обещал выучить малую таблицу!) его значение:
\( \displaystyle cos\ 60{}^\circ =0,5\)
Тогда получим окончательный ответ:
\( \displaystyle sin~\ 2130{}^\circ =-0,5\)
Ответ: \( \displaystyle -0,5\)
2. \( \displaystyle \sqrt{2}cos\frac{21\pi }{4}\)
Все то же самое, но вместо градусов – радианы. Ничего страшного. Главное помнить, что
\( \displaystyle \pi ~рад.=180{}^\circ \)
Но можно и не заменять радианы на градусы. Это вопрос твоего вкуса. Я не буду ничего менять. Начну опять-таки с отбрасывания целых кругов:
\( \displaystyle \frac{21\pi }{4}=5\frac{1}{4}\pi =4\pi +1\frac{1}{4}\pi \)
Отбрасываем \( \displaystyle 4\pi \) – это два целых круга. Осталось вычислить \( \displaystyle cos\ 1\frac{1}{4}\pi \).
3. \( \displaystyle 12\sin 150{}^\circ \cos 120{}^\circ \).
Нужно проделать все то же самое, но уже с двумя функциями.
Я буду несколько более краток: \( \displaystyle 150{}^\circ \) и \( \displaystyle 120{}^\circ \) градусов – углы второй четверти. Косинус второй четверти имеет знак «минус», а синус – «плюс».
\( \displaystyle 150{}^\circ \) можно представить как: \( \displaystyle 150{}^\circ =90{}^\circ +60{}^\circ \), а \( \displaystyle 120{}^\circ \) как \( \displaystyle 90{}^\circ +30{}^\circ \), тогда:
10 примеров на тренировку
Реши эти 10 заданий, и ты научишься пользоваться формулами тригонометрии!
Ну вот, теперь на мой взгляд, ты готов к решению всех оставшихся «за бортом» задач. Страшные углы теперь тебе более не помеха. Попробуй прорешать примеры самостоятельно, а потом мы с тобой сравним результаты.
- \( \displaystyle \frac{5cos29{}^\circ }{sin61{}^\circ }\)
- \( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}\)
- \( \displaystyle -4\sqrt{3}\text{cos}\left( -750{}^\circ \right)\)
- \( \displaystyle 2\sqrt{3}tg\left( -300{}^\circ \right)\)
- \( \displaystyle \frac{14sin409{}^\circ }{sin49{}^\circ }\)
- \( \displaystyle \frac{12}{si{{n}^{2}}27{}^\circ +co{{s}^{2}}207{}^\circ }\)
- \( \displaystyle \frac{5sin74{}^\circ }{cos37{}^\circ cos53{}^\circ }\)
- \( \displaystyle \sqrt{3}co{{s}^{2}}\frac{5\pi }{12}-\sqrt{3}si{{n}^{2}}\frac{5\pi }{12}\)
- Найдите значение выражения \( \displaystyle 5tg\left( 5\pi -\gamma \right)-tg\left( -\gamma \right)\), если \( \displaystyle tg\gamma =7\).
- Найдите \( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)\), если \( \displaystyle sin\alpha =0,8\) и \( \displaystyle \alpha \in \left( \frac{\pi }{2};\pi \right)\).
Решения:
1. \( \displaystyle \frac{5cos29{}^\circ }{sin61{}^\circ }\)
Ключ к успеху – заметить, что:
\( \displaystyle 29{}^\circ +61{}^\circ =90{}^\circ \)!!!
Тогда, например \( \displaystyle 90{}^\circ -61{}^\circ =29{}^\circ \):
\( \displaystyle \frac{5cos29{}^\circ }{sin61{}^\circ }=\frac{5\text{cos}\left( 90{}^\circ -61{}^\circ \right)}{sin61{}^\circ }\)
\( \displaystyle 90{}^\circ -61{}^\circ \)– угол первой четверти. Косинус первой четверти – положительный. Поскольку мы вычитаем из \( \displaystyle 90\) градусов, то косинус меняется на синус:
\( \displaystyle \frac{5\text{cos}\left( 90{}^\circ -61{}^\circ \right)}{sin61{}^\circ }=\frac{5sin61{}^\circ }{sin61{}^\circ }=5\)
Ответ: \( \displaystyle 5\).
2. \( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}\)
\( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}\)
Опять задача целиком на формулы приведения. Вначале….
\( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}=\frac{8}{-\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2}}{2}}=\frac{8}{-\frac{2}{4}}=-8:\left( \frac{2}{4} \right)=-16\)
…избавимся от минуса, вынеся его перед синусом (поскольку синус – функция нечетная!!!). Затем рассмотрим углы:
\( \displaystyle \frac{27\pi }{4}=\frac{26\pi }{4}+\frac{\pi }{4}=6\pi +\frac{\pi }{4}\)
Отбрасываем целое количество кругов – то есть три круга (\( \displaystyle 6\pi \)). Остается вычислить: \( \displaystyle sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}\)
Так же поступаем и со вторым углом:
\( \displaystyle \frac{31\pi }{4}=7\frac{3}{4}\pi =7\pi +\frac{3}{4}\pi \)
Удаляем целое число кругов –3 круга (\( \displaystyle 6\pi \)) тогда:
\( \displaystyle \text{cos}\left( \frac{31\pi }{4} \right)=\cos \left( 7\pi +\frac{3}{4}\pi \right)=\cos \left( \pi +\frac{3}{4}\pi \right)\)
Теперь думаем: в какой четверти лежит оставшийся угол?
3. \( \displaystyle -4\sqrt{3}\text{cos}\left( -750{}^\circ \right)\)
Стандартно: убираем минус из косинуса, пользуясь тем, что \( \displaystyle cos\left( -x \right)=cos\left( x \right)\).
Осталось сосчитать косинус \( \displaystyle 750\) градусов. Уберем целые круги: \( \displaystyle 750{}^\circ =2\cdot 360{}^\circ +30{}^\circ \).
Тогда:
4. \( \displaystyle 2\sqrt{3}tg\left( -300{}^\circ \right)\)
\( \displaystyle 2\sqrt{3}tg\left( -300{}^\circ \right)\)Действуем так же, как в предыдущем примере.
\( \displaystyle \ tg\left( -300{}^\circ \right)=-tg300{}^\circ \)
Поскольку ты помнишь, что период у тангенса – \( \displaystyle 180\) градусов (или \( \displaystyle \pi \)) в отличие от косинуса или синуса, у которых он в 2 раза больше, то удалим целое количество \( \displaystyle \pi \).
5. \( \displaystyle \frac{14sin409{}^\circ }{sin49{}^\circ }\)
Снизу у нас все хорошо – маленький уголок первой четверти. Наверху же – все плохо.
Угол большой, надо его упростить по формулам приведения:
6. \( \displaystyle \frac{12}{si{{n}^{2}}27{}^\circ +co{{s}^{2}}207{}^\circ }\)
Вся проблема, как ты понимаешь, в косинусе. Но не беда, решим.
Смотри, на знак нам все равно, поскольку косинус-то у нас в квадрате и знак всегда будет «плюс».То есть на четверти можно не смотреть.
В то же время:
7. \( \displaystyle \frac{5sin74{}^\circ }{cos37{}^\circ cos53{}^\circ }\)
Пример немного похитрее. Прежде всего заметим, что \( \displaystyle 74{}^\circ =2\cdot 37{}^\circ \). Тогда давай представим числитель как синус двойного угла!
\( \displaystyle \frac{5sin74{}^\circ }{cos37{}^\circ cos53{}^\circ }=\frac{5\cdot 2sin37{}^\circ cos37{}^\circ }{cos37{}^\circ cos53{}^\circ }=\frac{10sin37{}^\circ }{cos53{}^\circ }\)
Тебе это ничего не напоминает? Задача в точности такая же, как в номере 1. Я тогда так и поступлю, заметив, что у меня опять:
8. \( \displaystyle \sqrt{3}co{{s}^{2}}\frac{5\pi }{12}-\sqrt{3}si{{n}^{2}}\frac{5\pi }{12}\)
Опять задание комбинированное! Легко увидеть и вынести за скобки общий множитель \( \displaystyle \sqrt{3}\):
\( \displaystyle \sqrt{3}co{{s}^{2}}\frac{5\pi }{12}-\sqrt{3}si{{n}^{2}}\frac{5\pi }{12}=\sqrt{3}\left( co{{s}^{2}}\frac{5\pi }{12}-si{{n}^{2}}\frac{5\pi }{12} \right)\)
Как называется формула внутри скобок? Пробегись глазами по списку наших формул! Нашел? Это косинус двойного угла!
9. Найдите значение выражения \( \displaystyle 5tg\left( 5\pi -\gamma \right)-tg\left( -\gamma \right)\), если \( \displaystyle tg\gamma =7\).
У тангенса период – \( \displaystyle \pi \), так что не задумываясь отбрасываем его:
\( \displaystyle 5tg\left( 5\pi -\gamma \right)=5tg\left( -\gamma \right)\ =-5tg\gamma \)
Здесь мы использовали еще и тот факт, что тангенс – функция нечетная.
10. Найдите \( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)\), если \( \displaystyle sin\alpha =0,8\) и \( \displaystyle \alpha \in \left( \frac{\pi }{2};\pi \right)\)
Вначале упростим выражение, используя формулы приведения (вначале отбросим целые круги и уберем минус):
\( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)=\sin \left( 2\pi -\frac{\pi }{2}-\alpha \right)=\sin \left( -\frac{\pi }{2}-\alpha \right)=-\text{sin}\left( \frac{\pi }{2}+\alpha \right)\)
Наш оставшийся угол – во третьей четверти (посмотри на условия для угла в условии задачи!!!).
Средний уровень сложности
В некоторых (не очень тривиальных) случаях, следующие формулы помогут тебе выйти из затруднительной ситуации.
Первая группа формул является универсальной: она позволяет перейти от любого тригонометрического выражения к рациональному.
Это, конечно, имеет важное приложение при решении уравнений, но здесь мы рассмотрим, как эти формулы помогают при упрощении тригонометрических выражений.
Формулы понижения степени
- \( \displaystyle {\sin^{2}}\alpha =\frac{1-\cos2\alpha }{2}\)
- \( \displaystyle {\cos^{2}}\alpha =\frac{1+\cos2\alpha }{2}\)
- \( \displaystyle t{{g}^{2}}\alpha =\frac{1-\cos2\alpha }{1+\cos2\alpha },\alpha \ne \frac{\pi }{2}+\pi n,n\in Z\)
Универсальная тригонометрическая подстановка
- \( \displaystyle \sin\alpha =\frac{2tg\frac{\alpha }{2}}{1+t{{g}^{2}}\frac{\alpha }{2}}\)
- \( \displaystyle \cos\alpha =\frac{1-t{{g}^{2}}\frac{\alpha }{2}}{1+t{{g}^{2}}\frac{\alpha }{2}}\)
- \( \displaystyle tg\alpha =\frac{2tg\frac{\alpha }{2}}{1-t{{g}^{2}}\frac{\alpha }{2}}\)
- \( \displaystyle ctg\alpha =\frac{1-t{{g}^{2}}\frac{\alpha }{2}}{2tg\frac{\alpha }{2}}\)
В чем прелесть этих формул? Первые две позволяют «убрать степени», то есть понизить порядок выражения (или повысить, за счёт снижения кратности угла), вторая группа формул позволяет свести любое тригонометрическое выражение к виду, зависящему только от тангенсов!
Иногда это единственный способ решить ту или иную задачу.
Разбор 3 примеров
1. Доказать тождество: \( \displaystyle \frac{3-4\cos2\alpha +\cos4\alpha }{3+4\cos2\alpha +\cos4\alpha }=t{{g}^{4}}\alpha \)
С виду тождество угрожающе! Но разберёмся по порядку. Формулы понижения степени, конечно, если их прочитать задом наперёд повышают степень!
И вообще, приглядись внимательно: первые две формулы есть ничто иное, как косинус двойного угла, записанный в несколько странной форме!
Вот и распишем по правилам:
\( \displaystyle \begin{array}{l}\frac{3-4\cos2\alpha +\cos4\alpha }{3+4\cos2\alpha +\cos4\alpha }=\frac{3-4\cos2\alpha +\left( 2{\cos^{2}}2\alpha -1 \right)}{3+4\cos2\alpha +\left( 2{\cos^{2}}2\alpha -1 \right)}=\\=\frac{2-4\cos2\alpha +2{\cos^{2}}2\alpha }{2+4\cos2\alpha +2{\cos^{2}}2\alpha }=\frac{1-2\cos2\alpha +{\cos^{2}}2\alpha }{1+2\cos2\alpha +{\cos^{2}}2\alpha }\end{array}\)
Тебе ничего по форме не напоминают числитель и знаменатель дроби? Приглядись внимательно, здесь «зарыта» хорошо известная тебе формула. Увидел её? Это же квадрат разности и квадрат суммы! (Подробнее об этом читай в статье о формулах сокращенного умножения)
\( \displaystyle \frac{1-2\cos2\alpha +{\cos^{2}}2\alpha }{1+2\cos2\alpha +{\cos^{2}}2\alpha }=\frac{{{\left( 1-\cos2\alpha \right)}^{2}}}{{{\left( 1+\cos2\alpha \right)}^{2}}}={{\left( \frac{1-\cos2\alpha }{1+\cos2\alpha } \right)}^{2}}\)
А выражение в скобках есть ничто иное, как \( \displaystyle t{{g}^{2}}\alpha \), окончательно получим:
\( \displaystyle {{\left( \frac{1-\cos2\alpha }{1+\cos2\alpha } \right)}^{2}}={{\left( t{{g}^{2}}\alpha \right)}^{2}}=t{{g}^{4}}\alpha \)
Тождество доказано!
Следующий пример очень схож с предыдущим, постарайся решить его самостоятельно.
2. Доказать тождество: \( \displaystyle \frac{1+\sin2\alpha +\cos2\alpha }{1+\sin2\alpha -\cos2\alpha }=ctg\alpha \)
Решение (хотя может и отличаться от твоего):
Опять «повысим степень» у косинуса: \( \displaystyle \cos2\alpha =2{\cos^{2}}\alpha -1\)
\( \displaystyle \frac{1+\sin2\alpha +\cos2\alpha }{1+\sin2\alpha -\cos2\alpha }=\frac{1+\sin2\alpha +2{\cos^{2}}\alpha -1}{1+\sin2\alpha -2{\cos^{2}}\alpha +1}=\frac{\sin2\alpha +2{\cos^{2}}\alpha }{2+\sin2\alpha -2{\cos^{2}}\alpha }\)
Надо сокращать дальше! Что делать? Ясно, что надо избавляться от двойных углов у синуса. Действуем по формуле синуса двойного угла и сокращаем двойки:
\( \displaystyle \frac{\sin2\alpha +2{\cos^{2}}\alpha }{2+\sin2\alpha -2{\cos^{2}}\alpha }=\frac{2\sin{\alpha} \cos{\alpha} +2{\cos^{2}}\alpha }{2+2\sin{\alpha} \cos{\alpha}-2{\cos^{2}}\alpha }=\frac{\sin\alpha \cos\alpha +{\cos^{2}}\alpha }{1+\sin\alpha \cos{\alpha}-{\cos^{2}}\alpha }\)
Числитель раскладывается на множители. Знаменатель –пока нет. До тех пор, пока мы не применим основное тригонометрическое тождество:
\( \displaystyle 1-{\cos^{2}}\alpha ={\sin^{2}}\alpha \)
\( \displaystyle \frac{\sin\alpha \cos\alpha +{\cos^{2}}\alpha }{1+\sin\alpha \cos\alpha -{\cos^{2}}\alpha }=\frac{\sin\alpha \cos\alpha +{\cos^{2}}\alpha }{{\sin^{2}}\alpha +\sin\alpha \cos\alpha }=\frac{\cos\alpha \left( \sin\alpha +\cos\alpha \right)}{\sin\alpha \left( \sin\alpha +\cos\alpha \right)}=ctg\alpha \)
Вот ещё один пример, но не такой простой.
3. Доказать, что если \( \displaystyle 0<\alpha <\frac{\pi }{2}\), то \( \displaystyle \sqrt{1+\sin\alpha }-\sqrt{1-\sin\alpha }=2\sin\frac{\alpha }{2}\)
Зачем нам дан угол? Наверное, чтобы оценить выражения: синус \( \displaystyle \alpha \)будет положительным, \( \displaystyle \sin\frac{\alpha }{2}>0,~1+\sin\alpha >1,~0<1-\sin\alpha <1\)
Тогда и левая, и правая части тождества больше нуля. Это даёт мне право без задней мысли возвести их в квадрат:
\( \displaystyle {{\left( \sqrt{1+\sin\alpha }-\sqrt{1-\sin\alpha } \right)}^{2}}=4{\sin^{2}}\frac{\alpha }{2}\) – вот такое тождество нам нужно теперь доказать.
Раскроем скобки в левой части по формуле квадрата разности!
\( \displaystyle \begin{array}{l}{{\left( \sqrt{1+\sin \alpha }-\sqrt{1-\sin \alpha } \right)}^{2}}=1+\sin \alpha -2\sqrt{1+\sin \alpha }\cdot \sqrt{1-\sin \alpha }+1-\\-\sin \alpha =2-2\sqrt{1+\sin \alpha }\cdot \sqrt{1-\sin \alpha }=2\left( 1-\sqrt{1+\sin \alpha }\cdot \sqrt{1-\sin \alpha } \right)=\\2\left( 1-\sqrt{1-{{\sin }^{2}}\alpha } \right)=2\left( 1-\sqrt{{\cos^{2}}}\alpha \right)\end{array}\)
Я не сомневаюсь в твоей грамотности и поэтому даже не упоминаю про использованные мною формулы в выкладках.
Теперь надо бы убрать корень из косинуса. Но мы знаем, что просто так это делать нельзя, ибо \( \displaystyle \sqrt{{{a}^{2}}}=\left| a \right|\).
В то же время вспоминаем про четверть: наш угол лежит в первой четверти, тогда косинус имеет знак «плюс» и мы просто убираем корень:
\( \displaystyle 2\left( 1-\sqrt{{\cos^{2}}}\alpha \right)=2\left( 1-\cos\alpha \right)\)
Тогда нам надо доказать, что
\( \displaystyle 2\left( 1-\cos\alpha \right)=4{\sin^{2}}\frac{\alpha }{2}\)
\( \displaystyle \left( 1-\cos\alpha \right)=2{\sin^{2}}\frac{\alpha }{2}\)
Справа применим формулу понижения степени:
\( \displaystyle {\sin^{2}}\frac{\alpha }{2}=\frac{1-\cos\alpha }{2}\), тогда \( \displaystyle 2{\sin^{2}}\frac{\alpha }{2}=1-\cos\alpha \)
Тождество доказано!
Конечно, можно привести ещё массу примеров, где применяются формулы понижения степени, ты их и сам без труда отыщешь.
Теперь вторая (и заключительная в этом обзоре) группа формул – формулы преобразования произведения в сумму и суммы в произведение.
Формулы преобразования суммы функций
- \( \displaystyle \sin\alpha \pm \sin\beta =2\sin\frac{\alpha \pm \beta }{2}\cos\frac{\alpha \mp \beta }{2}\)
- \( \displaystyle \cos\alpha +\cos\beta =2\cos\frac{\alpha +\beta }{2}\cos\frac{\alpha -\beta }{2}\)
- \( \displaystyle \cos\alpha -\cos\beta =-2\sin\frac{\alpha +\beta }{2}\sin\frac{\alpha -\beta }{2}\)
- \( \displaystyle tg\alpha \pm tg\beta =\frac{\sin\left( \alpha \pm \beta \right)}{\cos\alpha \cos\beta }\)
- \( \displaystyle ctg\alpha \pm ctg\beta =\frac{\sin\left( \beta \pm \alpha \right)}{\sin\alpha \sin\beta }\)
Иногда бывают полезны и обратные преобразования.
Формулы преобразования произведений функций
- \( \displaystyle \sin\alpha \sin\beta =\frac{\cos \left( \alpha -\beta \right)-\cos\left( \alpha +\beta \right)}{2}\)
- \( \displaystyle \sin\alpha \cos\beta =\frac{\sin \left( \alpha +\beta \right)+\sin\left( \alpha -\beta \right)}{2}\)
- \( \displaystyle \cos\alpha \cos\beta =\frac{\cos \left( \alpha -\beta \right)+\cos\left( \alpha +\beta \right)}{2}\)
Решение 5 примеров
1. Доказать тождество: \( \displaystyle \frac{\sin\alpha +\sin3\alpha }{\cos\alpha +\cos3\alpha }=tg2\alpha \)
Давай не будем долго думать, а, как говорится, пойдём в лобовую атаку: в числителе и знаменателе перейдём от суммы к произведению:
\( \displaystyle \begin{array}{l}~\frac{\sin\alpha+\sin3\alpha}{\cos\alpha+\cos3\alpha}=\frac{2\sin\frac{\alpha+3\alpha}{2}\cos\frac{\alpha-3\alpha}{2}}{2\cos\frac{\alpha+3\alpha}{2}\cos\frac{\alpha-3\alpha}{2}}=\frac{2\cdot \sin2\alpha\cdot \cos\left( -\alpha \right)}{2\cdot \cos2\alpha\cdot \cos\left( -\alpha \right)}=\\=\frac{\sin2\alpha}{\cos2\alpha}=tg2\alpha\end{array}\)
И минуты не прошло, а пример уже решён!
Теперь попробуй сам.
2. Доказать тождество: \( \displaystyle \frac{\sin2\alpha +\sin4\alpha }{\cos2\alpha -\cos4\alpha }=ctg\alpha \)
Решение – опять лобовая атака:
\( \displaystyle \begin{array}{l}\frac{\sin2\alpha+\sin4\alpha}{\cos2\alpha-\cos4\alpha}=\frac{2\sin\frac{2\alpha+4\alpha}{2}\cos\frac{2\alpha-4\alpha}{2}}{-2\sin\frac{2\alpha+4\alpha}{2}\sin\frac{2\alpha-4\alpha}{2}}=\frac{2\sin3\alpha\cdot \cos\left( -\alpha \right)}{-2\sin3\alpha\cdot \sin\left( -\alpha \right)}=\frac{\cos\left( -\alpha \right)}{-\sin\left( -\alpha \right)}\end{array}\)
Так как синус – функция нечётная, а косинус – чётная, то:
Этот пример чуть похитрее, будь внимателен!
3. Доказать тождество: \( \displaystyle \frac{\sin2\alpha +\sin5\alpha -\sin3\alpha }{\cos\alpha +1-2{\sin^{2}}2\alpha }=2\sin\alpha \)
Я не хочу трогать синус двойного угла. Уж больно он удобно раскладывается на множители, чего не скажешь о синусе тройного и тем более пятикратного угла.
Поэтому я сверну в произведение последние 2 слагаемых в числителе:
\( \displaystyle \begin{array}{l}\frac{\sin2\alpha +\sin5\alpha -\sin3\alpha }{\cos\alpha +1-2{\sin^{2}}2\alpha }=\frac{\sin2\alpha +2\sin\frac{5\alpha -3\alpha }{2}\cos\frac{5\alpha +3\alpha }{2}}{\cos\alpha +1-2{\sin^{2}}2\alpha }=\\=\frac{2\sin\alpha \cos\alpha +2\sin\alpha \cos4\alpha }{\cos\alpha +1-2{\sin^{2}}2\alpha }=\frac{2\sin\alpha \left( \cos\alpha +\cos4\alpha \right)}{\cos\alpha +1-2{\sin^{2}}2\alpha }\end{array}\)
Конечно, теперь можно было бы и свернуть числитель ещё раз, но я пойду иным путём. В знаменателе у меня тоже спрятана формула, вот она:
\( \displaystyle 1-2{\sin^{2}}2\alpha \).
Что это за формула? Это косинус двойного угла!
\( \displaystyle 1-2{\sin^{2}}2\alpha =\cos\left( 2\cdot 2\alpha \right)=\cos4\alpha \)
\( \displaystyle \frac{2\sin\alpha \left( \cos\alpha +\cos4\alpha \right)}{\cos\alpha +1-2{\sin^{2}}2\alpha }=\frac{2\sin\alpha \left( \cos\alpha +\cos4\alpha \right)}{\cos\alpha +\cos4\alpha }=2\sin\alpha \)
Тождество доказано!
Теперь попробуй решить вот этот пример для закрепления пройденного материала.
4. Доказать тождество: \( \displaystyle {\cos^{4}}\alpha -{\sin^{4}}\alpha +\sin2\alpha =\sqrt{2}\cos\left( 2\alpha -\frac{\pi }{4} \right)\)
Проверяем!
\( \displaystyle \begin{array}{l}{\cos^{4}}\alpha -{\sin^{4}}\alpha +\sin2\alpha =\left( {\cos^{2}}\alpha -{\sin^{2}}\alpha \right)\left( {\cos^{2}}\alpha +{\sin^{2}}\alpha \right)+\sin2\alpha =\\=\cos2\alpha +\sin2\alpha \end{array}\)
C другой стороны:
\( \displaystyle \begin{array}{l}\sqrt{2}\cos \left( 2\alpha-\frac{\pi }{4} \right)=\sqrt{2}\left( \cos{2\alpha}\cos{\frac{\pi }{4}}+\sin{2\alpha}\sin{\frac{\pi }{4}} \right)=\\=\sqrt{2}\left( \frac{\sqrt{2}}{2}\cos2\alpha+\frac{\sqrt{2}}{2}\sin2\alpha \right)=\sqrt{2}\cdot \frac{\sqrt{2}}{2}\left( \cos2\alpha+\sin2\alpha \right)=\\=\cos2\alpha+\sin2\alpha\end{array}\)
Тождество доказано!
На этом примере я буду закругляться потихоньку.
Сразу оговорюсь: не переживай и не волнуйся, если у тебя что-то сразу не выходит. Тригонометрия – сложная и очень обширная тема. Здесь все зависит не только от знания формул, но и от мастерства и смекалки. На их выработку тебе понадобится время и усердие.
Более того, скажу тебе вот что: изначально я хотел вставить другой пример в качестве заключительного. Однако на его решение мне понадобилось около 20 минут, причём я использовал ещё более сложную методику его решения. Так что не только ты сталкиваешься с трудностями при решении примеров, трудности бывают у всех!
Все-таки я приведу здесь этот трудный пример, вдруг да и получится у тебя решить его, может, я что-то упустил. Вот он:
5. Упростить: \( \displaystyle \frac{1+\sin\alpha -\cos2\alpha -\sin3\alpha }{2{\sin^{2}}\alpha +\sin\alpha -1}\)
А вот какой у меня получился в итоге ответ: \( \displaystyle 2\sin\alpha.\)
Дерзай!
В следующей части статьи я рассмотрю его решение, но прибегну к ещё более изощрённой технике нежели та, что рассматривалась здесь! Удачи!
Повышенный уровень сложности
В дополнение к уже изложенному материалу, я бы хотел рассмотреть еще небольшую группку формул, которая осталась «за бортом».
Эти формулы – некоторое обобщение уже рассмотренных ранее формул понижения степени, но вот понижаемые степени у них повыше.
Формулы понижения 3-й степени
- \( \displaystyle si{{n}^{3}}\alpha =\frac{3sin\alpha -sin3\alpha }{4}\)
- \( \displaystyle co{{s}^{3}}a=\frac{3cosa+cos3a}{4}\)
Из данных формул можно вывести формулы тройного угла.
Формулы тройного угла
- \( \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \)
- \( \displaystyle cos3a=4co{{s}^{3}}a-3cosa\)
- \( \displaystyle tg3\alpha =\frac{3tg\alpha -t{{g}^{3}}\alpha }{1-3t{{g}^{2}}\alpha }\)
- \( \displaystyle ctg3\alpha =\frac{3ctg\alpha -ct{{g}^{3}}\alpha }{1-3ct{{g}^{2}}\alpha }\)
Ты мне можешь задать резонный вопрос: как часто эти формулы используются? Я отвечу: постарайся избегать прибегать к ним. Они нужны на тот случай, когда ничего другого уже не можешь придумать.
В частности, они могут быть полезными при решении сложных уравнений, которые встречаются во вступительных экзаменах на математические специальности.
Однако уравнениям у нас будет посвящена отдельная статья, так что здесь я рассмотрю случаи, когда данные формулы позволяют упрощать тригонометрические выражения.
Пример 1
Упростить: \( \displaystyle A=\frac{1}{3}co{{s}^{3}}\alpha \cdot sin3\alpha +\frac{1}{3}si{{n}^{3}}\alpha \cdot cos3\alpha \)
Решение:
Подставим вместо \( \displaystyle sin3\alpha \) и \( \displaystyle cos3\alpha \) их представления согласно формулам тройного угла, тогда:
\( \displaystyle \begin{array}{l}A=\frac{1}{3}co{{s}^{3}}\alpha \left( 3sin\alpha -4si{{n}^{3}}\alpha \right)+\frac{1}{3}si{{n}^{3}}\alpha \left( 4co{{s}^{3}}\alpha -3cos\alpha \right)=\\=co{{s}^{3}}\alpha \cdot sin\alpha -\frac{4}{3}co{{s}^{3}}\alpha \cdot si{{n}^{3}}\alpha +\frac{4}{3}co{{s}^{3}}\alpha \cdot si{{n}^{3}}\alpha -si{{n}^{3}}\alpha \cdot cos\alpha =\\=co{{s}^{3}}\alpha \cdot sin\alpha -si{{n}^{3}}\alpha \cdot cos\alpha \end{array}\)
Теперь вынесем в оставшемся выражении общий множитель за скобки:
\( \displaystyle co{{s}^{3}}\alpha \cdot sin\alpha -si{{n}^{3}}\alpha \cdot cos\alpha =sin\alpha \cdot cos\alpha \left( co{{s}^{2}}\alpha -si{{n}^{2}}\alpha \right)\)
По формулам двойного угла: \( \displaystyle sin\alpha \cdot cos\alpha =\frac{1}{2}sin2\alpha \), \( \displaystyle co{{s}^{2}}\alpha -si{{n}^{2}}\alpha =cos2\alpha \):
\( \displaystyle sin\alpha \cdot cos\alpha \left( co{{s}^{2}}\alpha -si{{n}^{2}}\alpha \right)=\frac{1}{2}sin2\alpha \cdot cos2\alpha \)
Ну а здесь снова спрятан синус двойного угла:
\( \displaystyle \frac{1}{2}sin2\alpha \cdot cos2\alpha =\frac{1}{4}sin4\alpha \)
Ответ: \( \displaystyle A=\frac{1}{4}sin4\alpha \)
Следующий пример попробуй решить самостоятельно. Не уверен, что в нем обязательно использовать формулу тройного угла, но можно сделать и с ее помощью.
Пример 2
Упростить: \( \displaystyle \frac{1+sin\alpha -\cos^2{\alpha}-cos2\alpha -sin3\alpha }{2si{{n}^{2}}\alpha +sin\alpha -1}\)
Решение:
Моя цель – свести числитель дроби к выражению, зависящему только от синусов одиночного угла. Для этого я преобразую
\( \displaystyle \cos^2 {\alpha} =1-si{{n}^{2}}\alpha \)
\( \displaystyle cos2\alpha =1-2si{{n}^{2}}\alpha \)
\( \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \)
Имеем:
\( \displaystyle \begin{array}{l}\frac{1+sin\alpha -cos2\alpha -sin3\alpha }{2si{{n}^{2}}\alpha +sin\alpha -1}=\frac{1+sin\alpha -\left( 1-si{{n}^{2}}\alpha \right) -\left( 1-2si{{n}^{2}}\alpha \right)-\left( 3sin\alpha -4si{{n}^{3}}\alpha \right)}{2si{{n}^{2}}\alpha +sin\alpha -1}=\\=\frac{4si{{n}^{3}}\alpha +3si{{n}^{2}}\alpha -2sin\alpha -1}{2si{{n}^{2}}\alpha +sin\alpha -1}\end{array}\)
Казалось бы, стало еще хуже. Но это так кажется. Давай для удобства вычислений заменим \( \displaystyle sin\alpha =t\), тогда мне надо упростить дробь
\( \displaystyle \frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1}\)
Нижнее выражение разложим на множители:
\( \displaystyle 2{{t}^{2}}+t-1=\left( t+1 \right)\left( 2t-1 \right)\)
С верхним фокус сложнее. Мы не умеем с тобой решать кубические уравнения. Но мы хорошо играем в «угадайку».
Угадай-ка один корень уравнения \( \displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=0\). Угадал? Я угадал \( \displaystyle -1\).
Тогда по теореме Безу (которую ты, быть может, знаешь, а если не знаешь, то без проблем отыщешь сам) выражение \( \displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1\) делится без остатка на \( \displaystyle t+1\)
Разделим столбиком \( \displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1\) на \( \displaystyle t+1\). Я получу:
\( \displaystyle 4{{t}^{3}}+3{{t}^{2}}-2t-1=\left( t+1 \right)\left( 4{{t}^{2}}-t-1 \right)\)
В свою очередь \( \displaystyle 4{{t}^{2}}-t-1=4\left( t-\frac{1}{2} \right)\left( t+\frac{1}{4} \right)\)
Окончательно получим:
\( \displaystyle \begin{array}{l}\frac{4{{t}^{3}}+3{{t}^{2}}-2t-1}{2{{t}^{2}}+t-1}=\frac{4\left( t+1 \right)\left( t-\frac{1}{2} \right)\left( t+\frac{1}{4} \right)}{\left( t+1 \right)\left( 2t-1 \right)}=\frac{\left( t+1 \right)\left( 2t-1 \right)\left( 2t+0,5 \right)}{\left( t+1 \right)\left( 2t-1 \right)}=\\=2t+0,5\end{array}\)
Тогда исходное выражение можно упростить до: \( \displaystyle 2sinx+0,5\)
В завершение я приведу тебе пример одного уравнения, которое было предложено на психологический (???!!!) факультет одного из ВУЗов в 1990 году. Такие задачи называются задачи-гробы (никакая смекалка без знания конкретной формулы не позволит их решить):
Решить уравнение: \( \displaystyle \sqrt{3}co{{s}^{3}}x-3co{{s}^{2}}x-3\sqrt{3}cosx+1=0\)
Не сделав вот такую странную замену: \( \displaystyle cosx=tg\alpha \) решить его очень сложно. А с такой заменой у нас получится вот что:
\( \displaystyle \sqrt{3}t{{g}^{3}}\alpha -3t{{g}^{2}}\alpha -3\sqrt{3}tg\alpha +1=0\)
\( \displaystyle \sqrt{3}t{{g}^{3}}\alpha -3\sqrt{3}tg\alpha =3t{{g}^{2}}\alpha -1\)
\( \displaystyle \sqrt{3}(t{{g}^{3}}\alpha -3tg\alpha )=3t{{g}^{2}}\alpha -1\)
\( \displaystyle -\sqrt{3}\left( 3tg\alpha -t{{g}^{3}}\alpha \right)=-\left( 1-3t{{g}^{2}}\alpha \right)\)
\( \displaystyle \frac{\left( 3tg\alpha -t{{g}^{3}}\alpha \right)}{\left( 1-3t{{g}^{2}}\alpha \right)}=\frac{1}{\sqrt{3}}\)
А вот ради чего весь этот сыр-бор: \( \displaystyle \frac{\left( 3tg\alpha -t{{g}^{3}}\alpha \right)}{\left( 1-3t{{g}^{2}}\alpha \right)}=tg3\alpha \)
\( \displaystyle tg3\alpha =\frac{1}{\sqrt{3}}\)
Это уравнение уже несказанно легче решается. Скоро мы вместе в этом убедимся. Но тут проблема в обратной замене… Тем не менее, эта задача почти нерешаема без знания формулы тангенса тройного угла. Вот так вот.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 9. Тригонометрическая окружность, табличные значения
На этом уроке мы узнаем, что такое тригонометрическая окружность и насколько она важна для тригонометрии. М
ы увидим, что она — основной инструмент в тригонометрии: с её помощью можно вывести любую формулу и найти любые значения.
Мы поймем, как «работает» окружность — а значит, поймём тригонометрию в целом.
ЕГЭ 13б. Тригонометрическая окружность
Тригонометрическая окружность — это очень простой и эффективный инструмент для решения любой тригонометрической задачи. На этом уроке вы узнаете как пользоваться тригонометрической окружностью для решения пункта «б» из задачи №13 профильного ЕГЭ.
Пункт “б” задачи №13 ЕГЭ 2020 В 2020 году на ЕГЭ в пункте «б» необходимо было указать корни тригонометрического уравнения принадлежащие отрезку.
Вообще-то решать пункт “б” можно двумя способами: — отметить корни уравнения на единичной окружности (способ разобранный в этом видео); — через двойное неравенство.
И вы должны знать, что второй способ чуть дольше, чем первый, но зато вы сможете проще описать все ваши рассуждения и вам будет сложнее ошибиться.
И еще один плюс второго способа — его проще оформить, так, чтобы к вам не придрались на ЕГЭ.
Мы считаем второй способ (через двойное неравенство) более предпочтительным на ЕГЭ по математике, но теме не менее для глубокого понимания темы (что может выручить на ЕГЭ) необходимо разобраться и с первым способом
Подготовка к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Во втором блоке заданий после формул приведения похоже ошибка. Вы уверены, что во втором задании (разборе его) 26п/4 = 6п? Там (в том помежуточном действии) будет (7*4=28) 7п-п/4.
10. Найдите sin(7π2−α), если sinα=0,8 и α∈(π2;π)
Вопрос по этой задаче, в решении у вас отбрасывают 2п, но разве там не 4 пи отбрасывается.
И у вас написано » Наш оставшийся угол – во третьей четверти (посмотри на условия для угла в условии задачи!!!)» Разве это не вторая четверть ? α∈(π2;π)
Некоторые комментарии прошлых лет к этой статье:
Афруза
04 апреля 2019
Блин как класно мне очень понравилось
Антон
12 апреля 2019
Здравствуйте, учебник очень хороший, поэтому и купил. Хотел задать маленький вопросик. Вот правильный ход мыслей у меня: Sin(-300)=-sin(270+30)=-cos30=-(-корень из 3 на 2)= корень из 3 на 2? Получается два минуса, которые дают плюс? Верно? Спасибо)
Алексей Шевчук
23 мая 2019
Антон, спасибо, очень рад, что наш учебник помогает:) Пример ты решил верно.