Прямоугольный треугольник
Хей! Ты, наверно, знаешь, что треугольники – очень полезная штука. А местами даже таинственная. Сегодня мы раскроем все «тайны» о прямоугольном треугольнике.
Ну, хотя бы те, что возникают в математике и пригодятся тебе на ЕГЭ 🙂
А хочешь научиться решать задачи? Мы прикрутим в этот пост вебинары с нашего курса подготовки к ЕГЭ. Обязательно посмотри их и ты сможешь решить любую задачу на эту тему.
Поехали!
Прямоугольный треугольник — коротко о главном
Прямоугольный треугольник –треугольник, у которого один из углов – прямой (= \( \displaystyle {{90}^{\circ }}\)).
- \( \displaystyle a,\text{ }b\) — катеты
- \( \displaystyle c\) — гипотенуза
- В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: \( {{a}^{2}}+{{b}^{2}}={{c}^{2}}\).
Признаки равенства прямоугольных треугольников:
- по двум катетам: \( \displaystyle a={{a}_{1}},\ b={{b}_{1}}\)
- по катету и гипотенузе: \( \displaystyle a={{a}_{1}},\ c={{c}_{1}}\) или \( \displaystyle b={{b}_{1}},\ c={{c}_{1}}\)
- по катету и прилежащему острому углу: \( \displaystyle a={{a}_{1}},\) \( \displaystyle \angle \beta =\angle {{\beta }_{1}}\) или \( \displaystyle b={{b}_{1}},\) \( \displaystyle \angle \alpha =\ \angle {{\alpha }_{1}}\)
- по катету и противолежащему острому углу: \( \displaystyle a={{a}_{1}},\) \( \displaystyle \angle \alpha =\ \angle {{\alpha }_{1}}\) или \( \displaystyle b={{b}_{1}},\) \( \displaystyle \angle \beta =\angle {{\beta }_{1}}\)
- по гипотенузе и остром углу: \( \displaystyle c={{c}_{1}},\) \( \displaystyle \angle \alpha =\ \angle {{\alpha }_{1}}\) или \( \displaystyle c={{c}_{1}},\) \( \displaystyle \angle \beta =\angle {{\beta }_{1}}\).
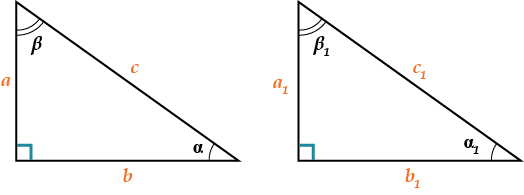
Признаки подобия прямоугольных треугольников:
- одному острому углу: \( \displaystyle \ \alpha =\ {{\alpha }_{1}}\) или \( \displaystyle \angle \beta =\angle {{\beta }_{1}}\)
- из пропорциональности двух катетов: \( \displaystyle \frac{a}{{{a}_{1}}}=\frac{b}{{{b}_{1}}}\)
- из пропорциональности катета и гипотенузы: \( \displaystyle \frac{a}{{{a}_{1}}}=\frac{c}{{{c}_{1}}}\) или \( \displaystyle \frac{b}{{{b}_{1}}}=\frac{c}{{{c}_{1}}}\).
Синус, косинус, тангенс, котангенс в прямоугольном треугольнике:
- Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе: \( \displaystyle \sin \ \alpha =\frac{a}{c},\ \ \sin \ \beta =\frac{b}{c}\)
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе: \( \displaystyle \cos \ \alpha =\frac{b}{c},\ \ \cos \ \beta =\frac{a}{c}\)
- Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему: \( \displaystyle tg\alpha =\frac{a}{b},\ \ tg\beta =\frac{b}{a}\)
- Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему: \( \displaystyle ctg\alpha =\frac{b}{a},\ \ ctg\beta =\frac{a}{b}\).
Высота прямоугольного треугольника
- Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника.
- Каждый из этих треугольников подобен исходному: \( \displaystyle \Delta BEC\sim \Delta AEC\sim \Delta ABC\)
- Высота прямоугольного треугольника: \( \displaystyle h=\frac{ab}{c}\) или \( \displaystyle h=\sqrt{BE\cdot EA}\).
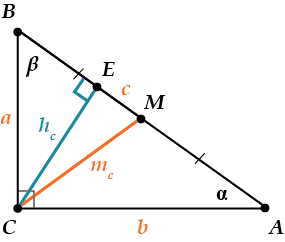
Медиана и описанная окружность
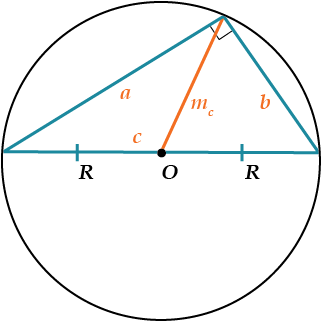
- В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: \( \displaystyle m=\frac{c}{2}\).
- Центр описанной окружности совпадает с серединой гипотенузы (точка О).
- Радиус описанной окружности: \( \displaystyle R=\frac{c}{2}={{m}_{c}}\).
Вписанная окружность
Радиус вписанной в прямоугольный треугольник окружности:
\( \displaystyle \begin{array}{l}r=\frac{ab}{a+b+c}\\r=\frac{1}{2}\left( a+b-c \right)\end{array}\)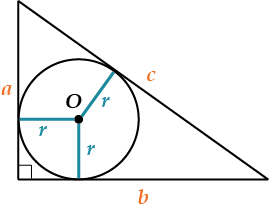
Площадь прямоугольного треугольника:
- через катеты: \( \displaystyle {{S}_{\Delta ABC}}=\frac{1}{2}ab\)
- через катет и острый угол: \( \displaystyle {{S}_{\Delta ABC}}=\frac{1}{2}{{a}^{2}}tg\beta =\frac{1}{2}{{a}^{2}}ctg\alpha \).
Прямоугольный треугольник — вебинар из курса подготовки к ЕГЭ
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.
Как это так?
Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно. Помните, понимать и уметь решать — это два, совершенно разных навыка.
Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.
Прямоугольный треугольник — определение
Что такое прямоугольный треугольник? Посмотри на картинку. Название говорит само за себя.
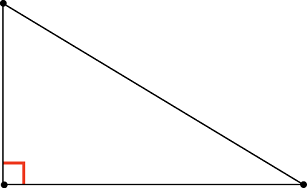
Прямоугольный треугольник – такой треугольник, один из углов которого прямой (то есть равен \( \displaystyle {{90}^{\circ }}\)).
В задачах прямой угол вовсе не обязательно – левый нижний, так что тебе нужно научиться узнавать прямоугольный треугольник и в таком виде:
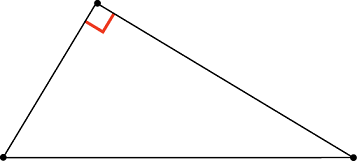
и в таком:
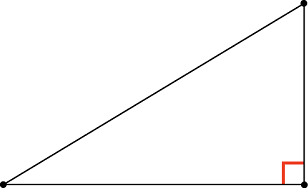
и в таком:
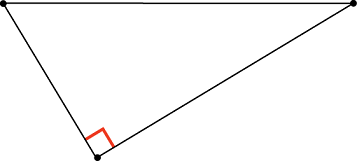
Что же хорошего есть в прямоугольном треугольнике? Ну, во-первых, есть специальные красивые названия для его сторон.
Стороны, между которыми прямой угол, называются катеты, а третья сторона (самая длинная) называется гипотенуза.
Внимание на рисунок!
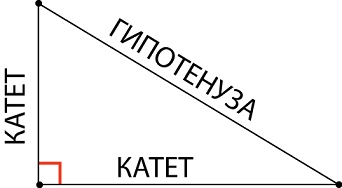
Запомни и не путай: катетов – два, а гипотенуза – всего одна (единственная, неповторимая и самая длинная)!
Ну вот, названия обсудили, теперь самое важное – теорема Пифагора.
Теорема Пифагора
Эта теорема – ключик к решению многих задачек с участием прямоугольного треугольника.
Её доказал Пифагор в совершенно незапамятные времена, и с тех пор она принесла много пользы знающим её. А самое хорошее в ней то, что она – простая.
Итак, теорема Пифагора:
Сумма квадратов катетов равна квадрату гипотенузы.
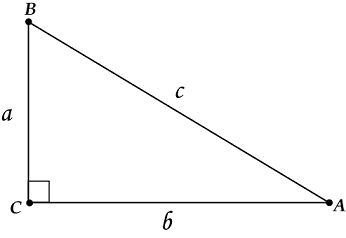
В буквах это так:
- \( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}\)
или так:
- \( {{c}^{2}}={{a}^{2}}+{{b}^{2}}\)
Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?
Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.
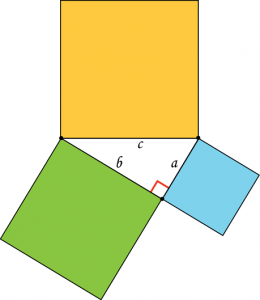
Правда, похоже на какие-то шорты? Ну и на какие стороны и где они равны? Почему и откуда возникла шутка? М-да… Кажется, у людей в античности с юмором явно проблемы.
Вовсе нет! А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:
«Сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе».
Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.
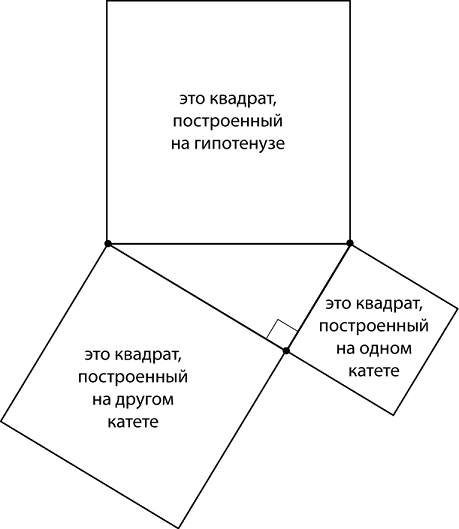
На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.
Почему же мы сейчас формулируем теорему Пифагора так:
\( {{c}^{2}}={{a}^{2}}+{{b}^{2}}\),

а Пифагор мучился и рассуждал про площади?
Понимаешь, в древние времена не было… алгебры! Не было никаких обозначений \( \displaystyle a,\text{ }b,\text{ }c,\text{ }x\) и так далее. Не было надписей \( \displaystyle {{a}^{2}},\text{ }{{b}^{2}},\text{ }{{c}^{2}}\).
Представляешь, как бедным древним ученикам было ужасно запоминать всё словами?! А мы можем радоваться, что у нас есть простая формулировка теоремы Пифагора 🙂
Давай её ещё раз повторим, чтобы лучше запомнить:
\( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}\)или
\( {{c}^{2}}={{a}^{2}}+{{b}^{2}}\)
Теперь уже должно быть легко:
Квадрат гипотенузы равен сумме квадратов катетов.
Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, то… сейчас мы ее докажем)
Доказательство теоремы Пифагора
Вполне возможно, что ты уже много раз использовал теорему Пифагора.
А вот задумывался ли ты, почему же верна такая теорема.
Как бы её доказать?
А давай поступим, как древние греки…
Нарисуем квадрат со стороной \( a+b\).
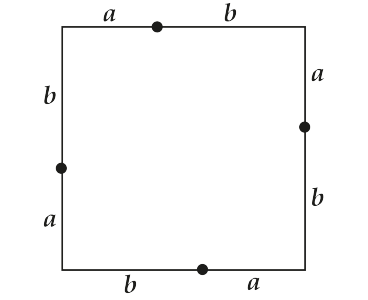
Видишь, как хитро мы поделили его стороны на отрезки длин \( a\) и \( b\)!
А теперь соединим отмеченные точки:
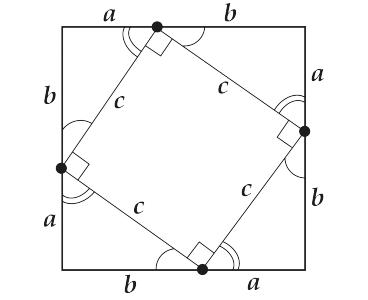
Тут мы, правда, ещё кое что отметили, но ты сам посмотри на рисунок и подумай, почему так.
Чему же равна площадь большего квадрата?
Правильно, \( {{\left( a+b \right)}^{2}}\).
А площадь меньшего?
Конечно, \( c^2\).
Осталась суммарная площадь четырех уголков. Представь, что мы взяли их по два и прислонили друг к другу гипотенузами.
Что получилось? Два прямоугольника. Значит, площадь «обрезков» равна \( \displaystyle 2ab\).
Давай теперь соберем всё вместе.
\( \displaystyle \underbrace{{{\left( a+b \right)}^{2}}}_{{{S}_{большого\ квадрата}}}=\underbrace{2ab}_{{{S}_{«обрезков»}}}+\underbrace{{{c}^{2}}}_{{{S}_{малого\ квадрата}} }\)Преобразуем: \( {{a}^{2}}+2ab+{{b}^{2}}=2ab+{{c}^{2}}\)
то есть \( {{a}^{2}}+{{b}^{2}}={{c}^{2}}\)
Вот и побывали мы Пифагором – доказали его теорему древним способом 🙂
Синус, косинус, тангенс, котангенс в прямоугольном треугольнике
На самом деле все совсем не так страшно.
Конечно, «настоящее» определение синуса, косинуса, тангенса и котангенса нужно смотреть в статье «Синус, косинус…».
Но очень не хочется, правда?
Можем обрадовать: для решения задач про прямоугольный треугольник можно просто заполнить следующие простые вещи:
- \( \sin \angle A=\frac{a}{c}\);
- \( \cos \angle A=\frac{b}{c}\);
- \( tg~\angle A=\frac{a}{b}\);
- \( ctg~\angle A=\frac{b}{a}\).

А почему же всё только про угол \( A\)? Где же угол \( B\)?
Для того, чтобы в этом разобраться, нужно знать, как утверждения 1 — 4 записываются словами.
Смотри, понимай и запоминай!
- \( \displaystyle \sin \angle A=\frac{a}{c}\)
Вообще-то звучит это так:
Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе.
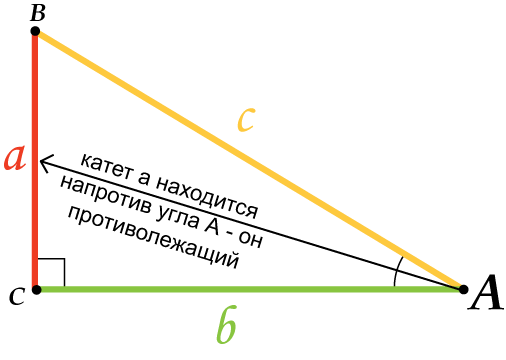
А что же угол \( \displaystyle B\)?
Есть ли катет, который находится напротив угла \( \displaystyle B\), то есть противолежащий (для угла \( \displaystyle B\)) катет?
Конечно, есть! Это катет \( \displaystyle b\)!
- Значит, \( \displaystyle \sin \angle B=\frac{b}{c}\)
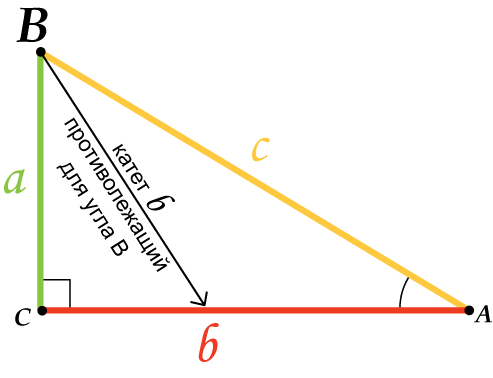
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
\( \displaystyle \cos \angle A=\frac{b}{c}\)Значит, \( \displaystyle \sin \angle B=\frac{b}{c}\)
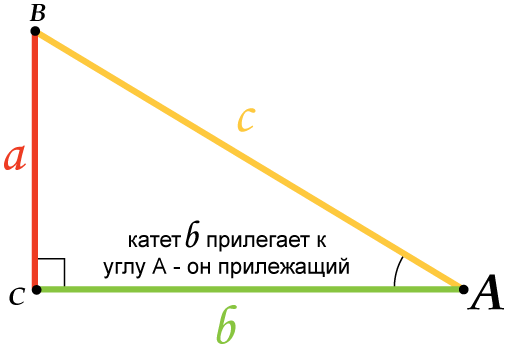
А как же угол \( \displaystyle B\)?
Посмотри внимательно. Какой катет прилегает к углу \( \displaystyle B\)? Конечно же, катет \( \displaystyle a\).
Значит, для угла \( \displaystyle B\) катет \( \displaystyle a\) – прилежащий, и
- \( \displaystyle \cos \angle B=\frac{a}{c}\).
А теперь, внимание! Посмотри, что у нас получилось:
\( \displaystyle \begin{array}{l}\sin \angle A=\frac{a}{c}\ \ \sin \angle B=\frac{b}{c}\ \ \\\cos \angle A=\frac{b}{c}\ \ \cos \angle B=\frac{a}{c}\end{array}\)
Видишь, как здорово:
\( \displaystyle \sin \angle A=\cos \angle B\) и \( \displaystyle \sin \angle B=\cos \angle A\)
Это очень удобно – если тебе дан в задаче синус одного угла прямоугольного треугольника, то ты знаешь и косинус другого!
Итак, запомни очень твёрдо:
В прямоугольном треугольнике синус одного острого угла равен косинусу другого и наоборот.
Теперь перейдём к тангенсу и котангенсу.
- \( \displaystyle tg~\angle A=\frac{a}{b}\)
Как это теперь записать словами?
Катет \( \displaystyle a\) каким является по отношению к углу \( \displaystyle A\)? Противолежащим, конечно – он «лежит» напротив угла \( \displaystyle A\).
А катет \( \displaystyle b\)? Прилегает к углу \( \displaystyle A\).
Значит, что у нас получилось?
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.

- \( \displaystyle ctg~\angle A=\frac{b}{a}\)
Видишь, числитель и знаменатель поменялись местами?
Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему.
Вспомним теперь про угол \( \displaystyle \angle B\). Что будет для него? Правильно:
- \( \displaystyle tg~\angle B=\frac{b}{a}\)\( \displaystyle ctg~\angle B=\frac{a}{b}\)

И теперь снова углы \( \displaystyle A\) и \( \displaystyle B\) совершили обмен:
\( \displaystyle \begin{array}{l}tg~\angle A=\frac{a}{b}\ \ tg~\angle B=\frac{b}{a}\\ctg~\angle A=\frac{b}{a}\ \ ctg~\angle B=\frac{a}{b}\end{array}\)
В прямоугольном треугольнике тангенс одного острого угла равен котангенсу другого.
Давай вкратце запишем всё, что мы узнали.
Промежуточный итог
Теорема Пифагора:
- \( \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}\)

I. \( \displaystyle \sin \angle A=\frac{a}{c};\ \ \sin \angle B=\frac{b}{c}\ \)
Синус острого угла равен отношению противолежащего катета к гипотенузе
II. \( \displaystyle \cos \angle A=\frac{b}{c};\ \ \cos \angle B=\frac{a}{c}\)
Косинус острого угла равен отношению прилежащего катета к гипотенузе.
III. \( \displaystyle tg~\angle A=\frac{a}{b};\ \ tg~\angle B=\frac{b}{a}\)
Тангенс острого угла равен отношению противолежащего катета к прилежащему катету.
IV. \( \displaystyle ctg~\angle A=\frac{b}{a};\ \ ctg~\angle B=\frac{a}{b}\)
Котангенс острого угла равен отношению прилежащего катета к противолежащему катету.
Заметил ли ты одну очень удобную вещь? Посмотри на табличку внимательно.
В прямоугольном треугольнике синус одного острого угла равен косинусу другого, а тангенс острого угла равен котангенсу другого.
А теперь тоже самое в виде таблички:
| \( \displaystyle \sin \angle A=\frac{a}{c}\) | \( \displaystyle \sin \angle B=\frac{b}{c}\) |
| \( \displaystyle \cos \angle A=\frac{b}{c}\) | \( \displaystyle \cos \angle B=\frac{a}{c}\) |
| \( \displaystyle tg~\angle A=\frac{a}{b}\) | \( \displaystyle tg~\angle B=\frac{b}{a}\) |
| \( \displaystyle ctg~\angle A=\frac{b}{a}\) | \( \displaystyle ctg~\angle B=\frac{a}{b}\) |
Запомни эту табличку как таблицу умножения – и ты сможешь решить много задач про прямоугольный треугольник.
Хотя… Можешь запомнить определения! А дальше можешь выразить это для любого угла!
Во всяком случае, все задачи первой части ЕГЭ, в которых участвует прямоугольный треугольник, тебе точно будут «по зубам»!
Признаки равенства прямоугольных треугольников
Признаков равенства прямоугольных треугольников всего четыре.
Ну еще надо чтобы треугольники были соответсвующие.
Смотри на рисунки и ты сразу запомнишь все 4 признака и сможешь применять их при решении задач.
P.S. Мы уже знаем, что к решению прямоугольных треугольников сводится абсолютное большинство задач геометрии. И это значит, что у тебя не будет с этим проблем.
Признаки равенства прямоугольных треугольников:
I. По двум катетам
Прямоугольные треугольники равны, если два катета одного треугольника соответственно равны двум катетам другого треугольника.
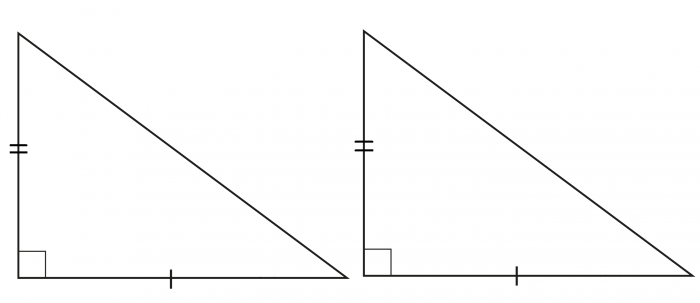
II. По катету и гипотенузе
Прямоугольные треугольники равны, если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого.
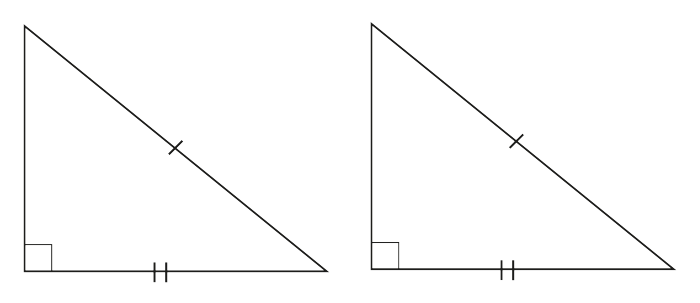
III. По гипотенузе и острому углу
Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого.
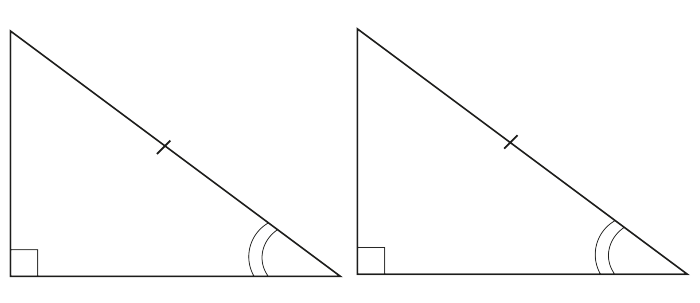
IV. По катету и острому углу
Прямоугольные треугольники равны, если катет и острый угол одного треугольника соответственно равны катету и острому углу другого треугольника.
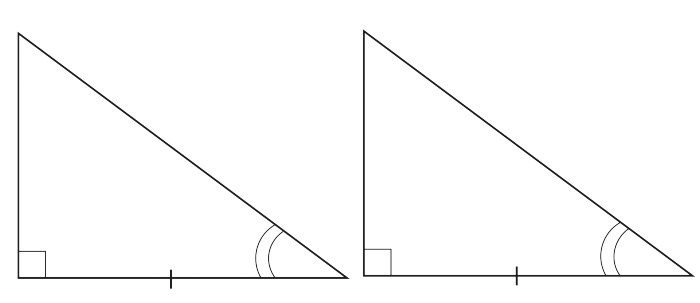
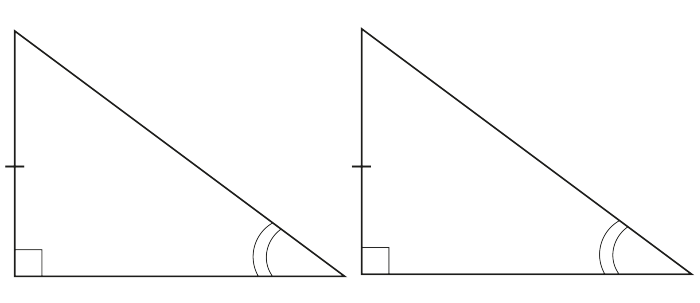
Внимание! Здесь очень важно, чтобы катеты были «соответствующие». Например, если будет так:
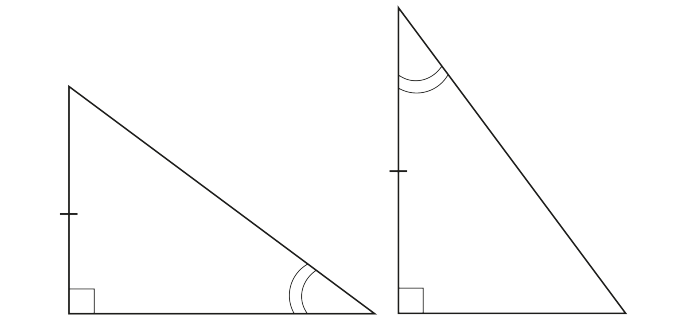
То треугольники не равны, несмотря на то, что имеют по одному одинаковому острому углу.
Нужно, чтобы в обоих треугольниках катет был прилежащим, или в обоих – противолежащим.
Ты заметил, чем отличаются признаки равенства прямоугольных треугольников от обычных признаков равенства треугольников?
Загляни в тему «Треугольник» и обрати внимание на то, что для равенства «рядовых» треугольников нужно равенство трех их элементов: две стороны и угол между ними, два угла и сторона между ними или три стороны.
А вот для равенства прямоугольных треугольников достаточно всего двух соответственных элементов. Здорово, правда?
Примерно такая же ситуация и с признаками подобия прямоугольных треугольников.
Признаки подобия прямоугольных треугольников
Признаков подобия прямоугольных треугольников тоже немного.
Только три — по острому углу, по двум катетам и по катету и гипотенузе.
Также смотри на рисунки и ты сразу все поймешь и запомнишь.
И сможешь применять при решении задач!
Признаки подобия прямоугольных треугольников
I. По острому углу
Если прямоугольные треугольники имеют по одинаковому острому углу, то они подобны.
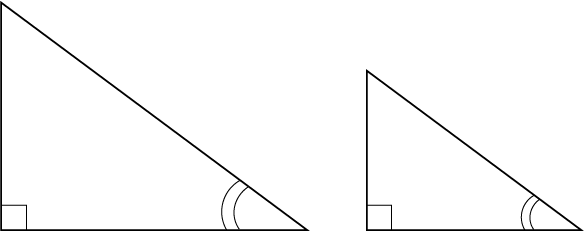
II. По двум катетам
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого, то эти треугольники подобны.
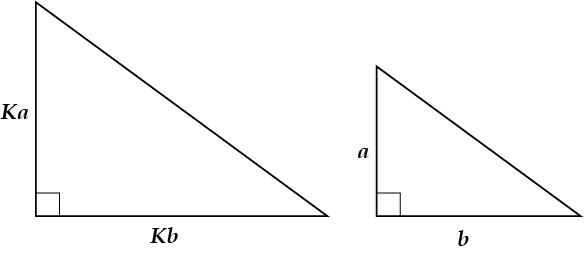
III. По катету и гипотенузе
Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого, то эти треугольники подобны.
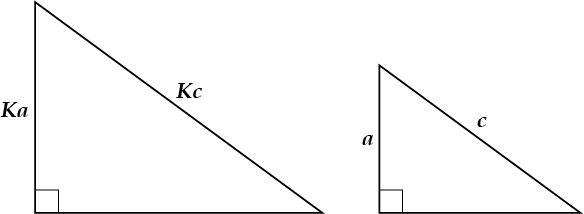
Медиана в прямоугольном треугольнике
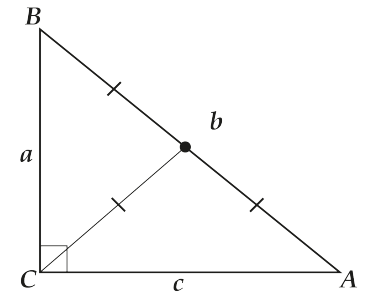
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы
Почему это так?
Рассмотрим вместо прямоугольного треугольника целый прямоугольник.
Что видим?
Треугольник \( \displaystyle ABC\) – половина прямоугольника.
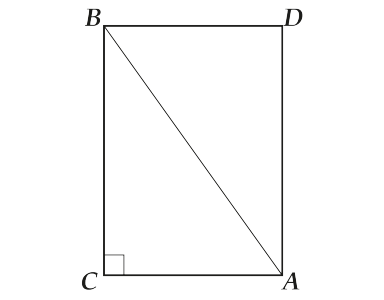
Проведём диагональ \( \displaystyle CD\) и рассмотрим точку \( \displaystyle O\) – точку пересечения диагоналей. Что известно про диагонали прямоугольника?
- Точкой пересечения диагонали делятся пополам
- Диагонали равны
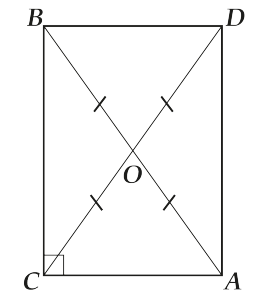
И что из этого следует?
- Точкой пересечения диагонали делятся пополам
Запомни этот факт! Очень помогает!
А что ещё более удивительно, так это то, что верно и обратное утверждение.
Если медиана, проведенная к какой-нибудь стороне треугольника, оказалась равна половине этой стороны, то треугольник – прямоугольный.
Что же хорошего можно получить из того, что медиана, проведенная к гипотенузе, равна половине гипотенузы?
А давай посмотрим на картинку.
Здесь\( \displaystyle CO\) – медиана и равна\( \frac{AB}{2}\).
Что же это получилось за точка \( \displaystyle O\)?
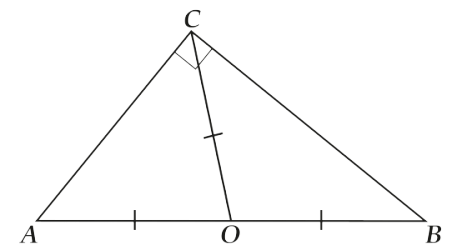
Посмотри внимательно. У нас есть: \( OA=OB=OC\), то есть расстояния от точки \( \displaystyle O\) до всех трёх вершин треугольника оказались равны. Но в треугольнике есть всего одна точка, расстояния от которой о всех трёх вершин треугольника равны, и это – ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ. Значит, что получилось?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Высота в прямоугольном треугольнике
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника.
Кроме того, каждый из этих треугольников подобен исходному.
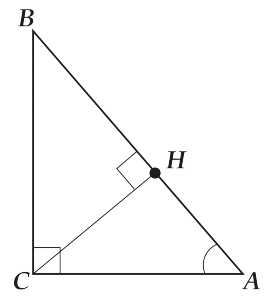
Вот давай мы начнём с этого «кроме того…».
Посмотрим на \( \Delta ABC\) и \( \Delta ACH\).
У них общий \( \angle A\), и они оба – прямоугольные. Значит (вспоминаем только что прочитанные признаки подобия прямоугольных треугольников) – они подобны!

Еще раз. \( \displaystyle \begin{array}{l}\Delta ABC,\ \Delta ACH:\\\left\{ \begin{array}{l}\angle CAB=\angle CAH\\\angle C=90{}^\circ ;\ \angle H=90{}^\circ \end{array} \right.\Rightarrow \\\Rightarrow \Delta ABC\sim \Delta ACH\end{array}\)

Но у подобных треугольников все углы равны!
\( \angle HCA=\angle CBA\) (Посмотри на рисунок)
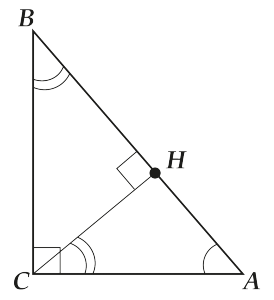
То же самое можно сказать и про \( \Delta CBH\) и \( \Delta ABC\)
А теперь нарисуем это вместе:
\( \displaystyle \begin{array}{l}\Delta ABC,\ \Delta CBH:\\\left\{ \begin{array}{l}\angle ABC=\angle CBH\\\angle C=90{}^\circ ;\ \angle H=90{}^\circ \end{array} \right.\Rightarrow \\\Rightarrow \Delta ABC\sim \Delta CBH\Rightarrow \\\Rightarrow \angle BAC=\angle BCH\end{array}\)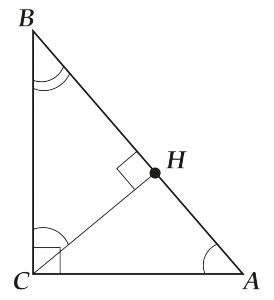
Что видим?
У \( \Delta BCH\) и \( \Delta CHA\) одинаковые острые углы!\( \displaystyle \Rightarrow \Delta BCH\sim \Delta CHA\)
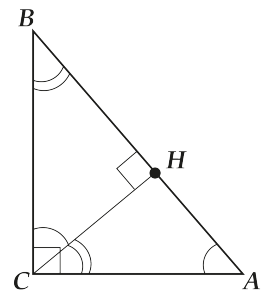
Какую же пользу можно извлечь из этого «тройственного» подобия.
Ну, например – две формулы для высоты прямоугольного треугольника.
Чтобы писать меньше букв, обозначим:
\( \displaystyle AC=b\);
\( \displaystyle BC=a\ \);
\( \displaystyle AB=c\);
\( \displaystyle CH=h\) (посмотри на рисунке).
Применяем подобие:\( \Delta ABC\sim \Delta ACH\).
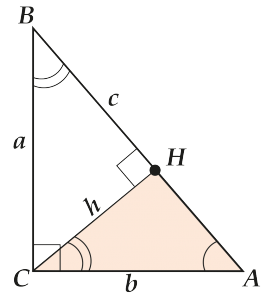
Запишем отношения соответствующих сторон:
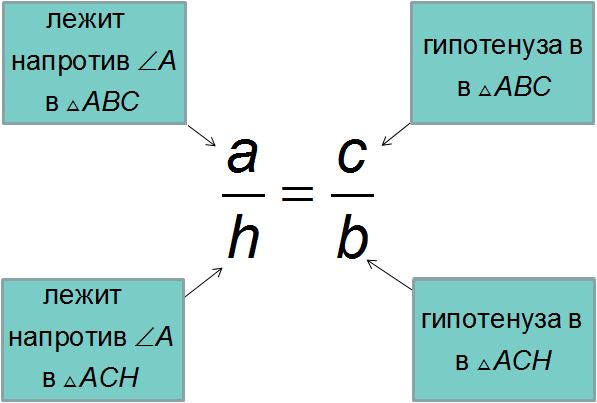
Для нахождения высоты решаем пропорцию и получаем первую формулу «Высота в прямоугольном треугольнике»:
\( \displaystyle h=\frac{ab}{c}\)
Как же получить вторую?
А теперь применим подобие треугольников \( BCH\) и \( CAH\).
Но сначала обозначим \( BH={{c}_{a}}\) и \( CH={{c}_{b}}\) ( смотри на рисунок)
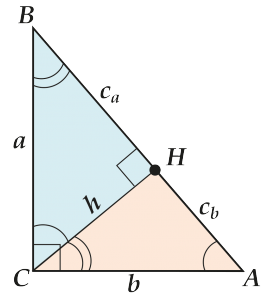
Итак, применим подобие: \( \displaystyle \Delta BCH\sim \Delta CAH\).
Значит,
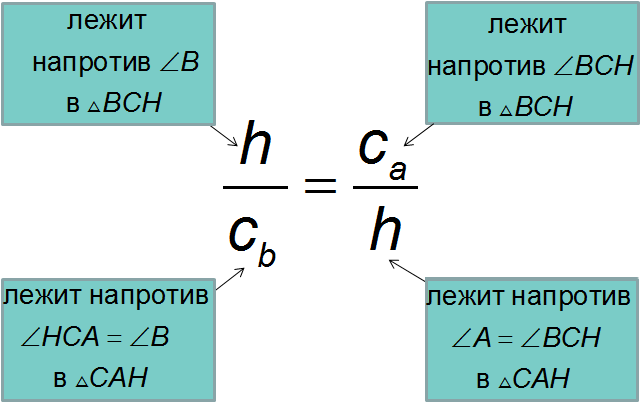
Что теперь получится?
Опять решаем пропорцию и получаем вторую формулу «Высота в прямоугольном треугольнике»:
\( \displaystyle {{h}^{2}}={{c}_{a}}{{c}_{b}}\) ,то есть \( \displaystyle h=\sqrt{{{c}_{a}}{{c}_{b}}}\)
Обе эти формулы нужно очень хорошо помнить и применять ту, которую удобнее.
Запишем их ещё раз:
\( \displaystyle h=\frac{ab}{c}\)
\( \displaystyle h=\sqrt{{{c}_{a}}{{c}_{b}}}\)
Ну вот, теперь, применяя и комбинируя эти знания с другими, ты решишь любую задачу с прямоугольным треугольником!
Бонус: Равнобедренные треугольники — вебинар из курса подготовки к ЕГЭ
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты.
Также мы научимся решать и «обычные» треугольники. Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Надежда
12 февраля 2019
Отлично изложено, спасибо!
Инна
07 марта 2019
Отличное объяснение и отличные советы в конце статьи! Спасибо!
Евгений
11 марта 2019
Очень хороший сайт. Рекомендую
Нина
14 марта 2019
Спасибо всем за такой увлекательный материал
Вова
18 сентября 2019
ХD для студента вроде меня очень полезная информация, когда мне рассказывали это в школе, я ничего не понял, но теперь мне всё более менее понятно, я даже на лету стал схватывать всё что читал дальше, Удачи !
Максмастер
18 ноября 2019
Есть такое слово-ТОЛКОВО !!!
Мухаммад
10 мая 2020
Почему учителя так понятно не объясняют???