Алгоритм определения площади и периметра сечения объемных фигур

1. Нарисовать сечение.
2. Определить фигуру, которая получилась в этом сечении.
3. Вспомнить формулы площади/периметра этой фигуры.
4. Найти площадь/периметр фигуры.

Стандартное сечение имеет вид треугольника, круга или четырехугольника. Следовательно, нам необходимо искать площади именно этих фигур.

Площадь сечения

Площадь треугольника

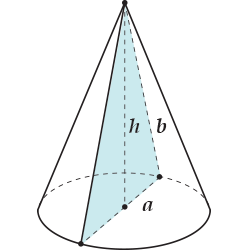
Площадь круга

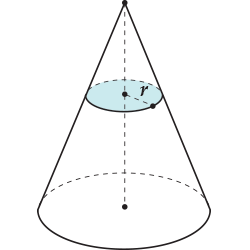
Площадь прямоугольника

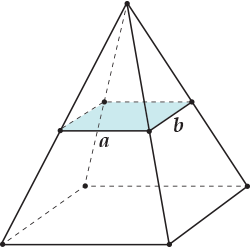
Пример решения задачи

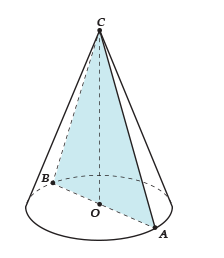
Диаметр основания конуса \( \displaystyle \left( AB \right)\) равен \( \displaystyle 8\) см.

Длина образующей \( \displaystyle \left( AC; BC \right)\) равна \( \displaystyle 5\) см (линия от вершины конуса до любой точки его основания).

Найдите площадь осевого сечения этого конуса.

Осевое сечение конуса – это равнобедренный треугольник \( \displaystyle \left( ABC \right)\), высота которого совпадает с высотой конуса \( \displaystyle \left( CO \right)\), а основание \( \displaystyle \left( AB \right)\) является диаметром основания конуса.

Значит, \( \displaystyle S\) осевого сечения конуса =\( \displaystyle S\) треугольника \( \displaystyle ABC\).

Вспомним формулу площади треугольника:

\( \displaystyle S=\frac{(CO\cdot AB)}{2}\ \)

\begin{matrix} AB\ -длина\ стороны\ треугольника \\ CO\ -\ высота,\ опущенная\ на \ сторону \ AB \\ \end{matrix}

Найдем высоту \( \displaystyle \Delta ABC\):

Рассмотрим \( \displaystyle \Delta COA\).

т.к. \( \displaystyle OC\) – высота \( \displaystyle \Delta ABC \rightarrow \angle COA=90{}^circ \rightarrow \Delta COA\) – прямоугольный.

\( \displaystyle AO=\frac{AB}{2}=\frac{8}{2}=4\) (т.к. \( \displaystyle AO\) – радиус окружности, \( \displaystyle AB\) – диаметр).

Найдем \( \displaystyle AC\):

По теореме Пифагора:

\( \displaystyle A{{C}^{2}}=C{{O}^{2}}+A{{O}^{2}}; C{{O}^{2}}=A{{C}^{2}}-A{{O}^{2}}={{5}^{2}}-{{4}^{2}}=9см; CO=\sqrt{9}=3см\)

Подставим получившиеся значения в формулу площади:

\( \displaystyle {{S}_{ABC}}=\frac{\left( CO\cdot AB \right)}{2}=\frac{3\cdot 8}{2}=\)\( \displaystyle 12см{{ }^{2}}\)

Площадь осевого сечения этого конуса равна \( \displaystyle 12см{{ }^{2}}\).