Системы уравнений. Начальный уровень.

Система уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных:

 

Методы решения систем уравнений:

1. Решение методом подстановки

Нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной, повторять подобную процедуру пока не будут найдены все переменные.

2. Решение графическим методом

Если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Графический метод – самый неточный. Практически его можно применять только для систем линейных уравнений (вида  ), графиками которых являются прямые. Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (только для иллюстраций).

3. Решение методом сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений.

То есть:

 

Но ни в коем случае не наоборот:

 

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.

Объединяем уравнения в систему с помощью фигурной скобки:

 

Система уравнений и методы ее решения

Метод подстановки

Это самый простой метод, но зачастую – самый трудоемкий. Идея проста – нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной.

Затем точно так же выражаем и подставляем другую переменную и т.д., пока не получим уравнение с одной переменной. После его решения и нахождения одной из переменных - последовательно возвращаемся к ранее выраженным, подставляя найденные значения.

Непонятно? Давай рассмотрим на примере

Пример 1.

 

Из второго уравнения очень просто выразить  :

 

Теперь подставим то, что получилось вместо   в первое уравнение:

 

Мы получили уравнение с одной неизвестной, которое очень просто решить:

 

 

 

 

 

А теперь вернемся к выраженному   и подставим в него полученное значение  :

 .

Итак,

Ответ:  

Ответ, кстати, принято записывать как координаты, то есть в таком виде:  . В случае трех неизвестных:  , и так далее.

То есть ответ в нашем примере запишется так:

Ответ:  

Попробуй сам решить несколько примеров методом подстановки:

1.  
2.  
3.  

Ответы:

1) Здесь проще всего выразить   из второго уравнения неравенства –

 

 , а затем подставить в первое.

 

Ответ:  

2) Выражаем   из второго уравнения и подставляем в первое.

Ответ:  

3) Здесь лучше выразить   из первого уравнения:

 

 , а затем уже подставлять во второе.

 

Ответ:  

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки. Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера. Для этого сперва выразим   в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно  ):

 

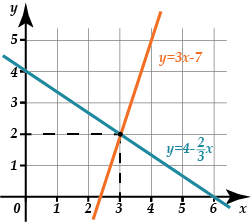
Видно, что графики пересекаются в точке с координатами  .

Графический метод – самый неточный. Практически его можно применять только для систем линейных уравнений (вида  ), графиками которых являются прямые. Если же хотя бы одно из уравнений имеет более сложный вид (содержит квадрат, корень, логарифм и т.д.), то не рекомендуется использовать графический метод (лучше использовать его только для иллюстраций).

Метод сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений. То есть:

 

(но ни в коем случае не наоборот:  )

Действительно, мы ведь имеем право прибавить к обеим частям уравнения одно и то же число, например, прибавим к первому уравнению число  :

 

Но раз  , в правой части можем заменить   на  :

 .

Пример 2

 

Сложим эти уравнения (левые части друг с другом, и правые – тоже друг с другом):

 .

Вот как!   просто уничтожился в результате сложения. Скажу сразу, это и была цель всего действия: складываем уравнения только тогда, когда при этом получим более простое уравнение.

Остается теперь только подставить в любое уравнение вместо   число  :

 

Ответ:  

Пример 3.

 

Очевидно, здесь сложение ничего не даст. Придется решать другим методом? Нет! Иначе метод сложения был бы полезен слишком редко. Мы ведь можем умножать любое уравнение на любое ненулевое число? Так давай умножим первое уравнение на такое число, чтобы потом при сложении какая-то переменная исчезла. Лучше всего умножить на  :

 

Теперь можно складывать:

 

 

Теперь подставим   в первое уравнение системы:

 

Ответ:  

Теперь порешай сам (методом сложения):

1.  
2.  
3.  
4.  

Ответы:

1. На что здесь надо умножить, чтобы коэффициенты при x или y были противоположными? Хм. Как из   получить   или из   получить  ? Умножать на дробное число? Слишком громоздко получится. Но ведь можно умножить оба уравнения! Например, первое на  , второе на  :

 

Теперь, сложив уравнения, мы можем легко найти  .

 

Подставляем в любое из уравнений и находим  .

Ответ: .

2. Решать нужно аналогично первому примеру – сначала нужно умножить первое уравнение на  , а второе на  , и сложить.

Ответ:  .

3. Первое умножаем на  , а второе на   и складываем.

Ответ:  .

4. Умножать можно и на дроби, то есть делить. Умножим первое уравнение на  , а второе на  :

 

Теперь сложим уравнения:

 

 

 

 

Подставив в первое уравнение, найдем  :

 

Ответ:  

Тренировка.

Теперь попробуй сам определить наиболее рациональный способ решения, а затем проверь ответы. Подсказок уже не будет!

1.  
2.  
3.  
4.  
5.  

Ответы:

1.  
2.  
3.  
4.  
5.  

Как видишь, система уравнений - базовая, но не самая сложная тема, используй методы, описанные в этой статье, и ты без труда справишься с решением систем.