Теорема косинусов (ЕГЭ 2022)
Что же такое теорема косинусов?
Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!
Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов 🙂
Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!
Поехали!
Теорема косинусов — коротко о главном
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
\( \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos \gamma \)

Почему теорема косинусов это… теорема Пифагора
И причем тут теорема Пифагора? Сейчас поясню.
Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
\( \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}\)

А что будет, если угол \( \displaystyle \angle C\), скажем, острый?

Вроде ясно, что величина \( \displaystyle {{c}^{2}}\) должна быть меньше, чем \( \displaystyle {{a}^{2}}+{{b}^{2}}\). Но вот на сколько меньше?
А если угол \( \displaystyle \angle C\) – тупой?

Ну, тогда величина \( \displaystyle {{c}^{2}}\) больше, чем \( \displaystyle {{a}^{2}}+{{b}^{2}}\)?
Но, опять же, на сколько? И как это связано с величиной \( \displaystyle \angle C\)?
Обрати внимание на вот эту добавку к теорему Пифагора: \( \displaystyle «-2ab\cos \gamma »\).
Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами.
Доказательство теоремы косинусов
Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.

Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
\( \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos \gamma \)
Рассмотрим три случая:
- угол С острый,
- угол С тупой,
- угол С прямой.
И убедимся, что для всех трех случаев теорема косинусов работает!
Угол С острый
\( \displaystyle \angle C<{{90}^{\circ }}\)
Проведем высоту \( \displaystyle AH\) из точки \( \displaystyle A\) и рассмотрим треугольник \( \displaystyle AHB\).
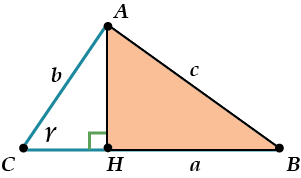
Он прямоугольный, можно пользоваться теоремой Пифагора:
\( \displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}}\)
Что такое \( \displaystyle AH\) и \( \displaystyle HB\) ?
\( \displaystyle AH\) можно выразить из треугольника (прямоугольного!) \( \displaystyle AHC\).
\( \displaystyle AH=b\sin \gamma \)
А вот \( \displaystyle BH=a-CH=a-b\cos \gamma \) (снова из \( \displaystyle \Delta AHC\) ).
Подставляем:
Угол С тупой
\( \displaystyle \angle C>{{90}^{\circ }}\)
Начинаем точно также: опускаем высоту из точки \( \displaystyle A\).
И снова:
\( \displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}}\)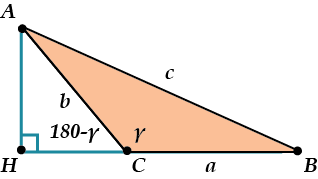
А теперь, внимание, отличие!
\( \displaystyle AH=b\sin \left( {{180}^{\circ }}-\gamma \right)\) — это из \( \displaystyle \Delta AHC\) , который теперь оказался снаружи \( \displaystyle \Delta ABC\), а
\( \displaystyle BH=a+b\cos \left( {{180}^{\circ }}-\gamma \right)\).
Вспоминаем, что:
Угол С прямой
\( \displaystyle \angle C={{90}^{\circ }}\).

Но тогда \( \displaystyle \cos \gamma =0\) и теорема косинусов просто превращается в теорему Пифагора:
\( \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}\).
В каких же задачах бывает полезна теорема косинусов?
Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.
Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:
\( \displaystyle {\cos \gamma =\frac{{{a}^{2}}+{{b}^{2}-{c}^{2}}}{2{a}{b}}}\)
И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.
Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.
И приходи к нам на бесплатные вебинары и занятия ( о них ниже).
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.
Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Ntpy_dame
31 октября 2019
Приятно оформленный сайт и хорошо изложенный материал, спасибо за ваш труд
Беслан
20 ноября 2019
Спасибо! Очень доступно
Лариса
23 января 2020
Спасибо! Более понятного объяснения не видела!