Задачи на смеси и сплавы
Задачи на смеси и сплавы очень простые.
Нужно уметь определять концентрацию вещества – это легко, это просто процент…
И понимать алгоритм решения – он тоже очень простой.
И все.
Ничего зубрить не нужно!
Задачи на смеси и сплавы — коротко о главном
Задачи на смеси и сплавы бывают двух видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
Масса раствора равна сумме масс всех составляющих.
При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Масса растворенного вещества при смешивании двух растворов суммируется.
Алгоритм решения задач на смеси и сплавы:
- Определить, какое вещество влияет на концентрацию раствора (главное вещество).
- Следить за весом главного вещества при добавлении других веществ в раствор.
- Исходя из данных об изменениях состояния главного вещества — сделать выводы.
Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на \( \displaystyle 100\), получим \( \displaystyle 1\%\) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на \( \displaystyle 100\%\).
Почему?
Сейчас покажу: пусть масса всего раствора равна \( \displaystyle M\), а масса растворенного вещества (например, соли или кислоты) – \( \displaystyle m\). Тогда один процент от массы раствора равен \( \displaystyle \frac{M}{100}\).
Как узнать, сколько таких процентов содержится в числе \( \displaystyle m\)?
Просто: поделить число \( \displaystyle m\) на этот один процент: \( \displaystyle \frac{m}{\frac{M}{100}}=\frac{m}{M}\cdot 100\), но ведь \( \displaystyle \frac{m}{M}\) – это концентрация.
Вот и получается, что ее надо умножить на \( \displaystyle 100\), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой \( \displaystyle 10\) кг содержится \( \displaystyle 3\) кг соли, то сколько в нем воды? Правильно, \( \displaystyle 7\)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой \( \displaystyle 10\) кг содержится \( \displaystyle 3\) кг кислоты, а во втором растворе массой \( \displaystyle 14\) кг – \( \displaystyle 5\) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
\( \displaystyle 10+14=24\) кг.
А сколько в новом растворе будет кислоты? \( \displaystyle 3+5=8\) кг.
Перейдем к задачам.
Решение задач на смеси и сплавы
Задачи на смеси и сплавы бывают двух основных видов:
- Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
- В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется.
Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
Давай попробуем решить несколько задачек. Попробуй решить каждую самостоятельно, а если не получится – посмотри в решение.
Задача №1
В \( \displaystyle 5\%\) раствор кислоты массой \( \displaystyle 3,8\) кг добавили \( \displaystyle 1,2\) кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решение
- Для начала вычислим, сколько кислоты содержится в \( \displaystyle 5\%\) растворе. Из \( \displaystyle 3,8\) кг \( \displaystyle 5\%\) — это кислота, а значит в растворе \( \displaystyle 0,05\cdot 3,8=0,19\ кг\) кислоты
- Далее определим массу нового раствора. Как мы уже знаем – масса раствора равна массе его составляющих, т.е. \( \displaystyle 3,8\) кг + \( \displaystyle 1,2\) кг = \( \displaystyle 5\) кг
- Поскольку в чистой воде кислоты нет, то в новом растворе количество кислоты не изменилось – \( \displaystyle 0,19\) кг. Таким образом, концентрация кислоты стала равна \( \displaystyle \frac{0,19}{5}=0,038\)
- Теперь выразим концентрацию в процентах — \( \displaystyle 0,038\cdot 100\%=3,8\%\)
Ответ: \( \displaystyle 3,8\).
Теперь давай попробуем решить задачу посложнее.
Задача №2
Смешали \( \displaystyle 3\) кг \( \displaystyle 5\%\)-го водного раствора щелочи и \( \displaystyle 7\) кг \( \displaystyle 15\%\)-го. Какова концентрация вновь полученного раствора? Ответ дайте в процентах.
Решение
Давай попробуем визуализировать ситуацию. \( \displaystyle 3\) кг \( \displaystyle 5\%\) водного раствора. Значит воды в этом растворе \( \displaystyle 95\%\).
Нарисуем:
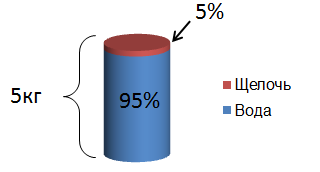
А теперь второй раствор:
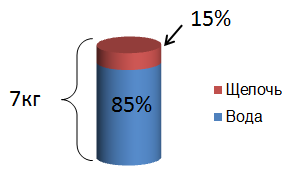
После смешивания, вновь получившийся раствор будет весить \( \displaystyle 3\) кг + \( \displaystyle 7\) кг = \( \displaystyle 10\) кг. Обозначим количество щелочи в новом растворе за \( \displaystyle x\), а количество воды – \( \displaystyle (10-x)\):
Задача №3
Чернослив содержит \( \displaystyle 25\%\) влаги. Его получают из сливы, содержащей \( \displaystyle 90\%\) влаги, путем сушки. Сколько нужно килограмм сливы, для получения \( \displaystyle 5\) кг чернослива?
Решение
Давай попробуем нарисовать:
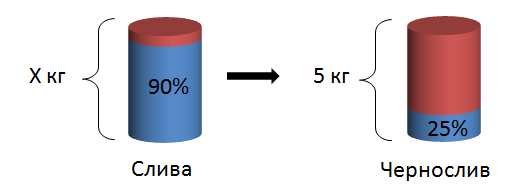
Теперь рассуждай:
Задача №4
Имеются два сплава серебра с медью. В первом содержится \( \displaystyle 10\%\) серебра, во втором – \( \displaystyle 25\%\). Сколько килограмм второго сплава нужно добавить к \( \displaystyle 10\)кг первого, чтобы получить сплав с \( \displaystyle 20\%\) содержанием серебра?
Решение:
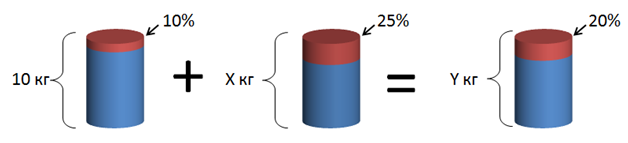
Подведем промежуточные итоги
Если ты заметил, во всех задачах мы сначала определяли, какое вещество влияет на концентрацию, назовем его «главным».
Дальше следили за абсолютной величиной этого главного вещества (в килограммах, литрах). Если в раствор (сплав) что-то доливали, добавляли, то, в зависимости от состава «добавки», вес «главного» вещества либо изменялся, либо нет.
Важно определить, что произошло с «главным» веществом, а дальше решение становится совсем простым.
5 задач на самостоятельную работу (с ответами)
А теперь попробуй решить несколько задач самостоятельно, и проверь ответы:
А теперь попробуй решить несколько задач самостоятельно, и проверь ответы:
- Имеются два сплава с содержанием цинка 15% и 22%. Какова будет концентрация цинка, если сплавить 90 кг первого и 50 кг второго.
- Сколько миллилитров 55% раствора уксуса нужно добавить к 500 миллилитрам 1% раствора, чтобы получить 5%раствор уксуса?
- Смешали некоторое количество 12% раствора вещества с таким же количеством 22% раствора этого же вещества. Какова концентрация (в процентах) вещества в новом растворе?
- В сосуд, содержащий 8 литров 14% раствора кислоты, добавили 12 литров воды. Сколько процентов кислоты содержится в новом растворе?
- Сколько килограмм 17% сплава меди нужно добавить к 5 килограммам 10% сплава меди, чтобы получить 12%сплав?
Ответы:
Задача №10
В \( \displaystyle 10\%\) раствор кислоты массой \( \displaystyle 3\) кг добавили \( \displaystyle 1,8\) кг чистой воды. Чему стала равна концентрация раствора (в процентах)?
Решил? Смотри:
- Вычисляем массу кислоты. Для этого запишем, что такое концентрация: \( \displaystyle \frac{m}{M}\cdot 100\%=10\%\text{ }\Rightarrow \text{ }\frac{m}{M}=0,1\text{ }\Rightarrow \text{ }m=0,1\cdot M=0,1\cdot 3=0,3\) кг. Впредь проценты всегда будем сразу записывать в виде десятичной дроби: \( \displaystyle 1\%=0,01\).
- Вычисляем массу нового раствора: \( \displaystyle 3+1,8=4,8\) кг.
- Новая концентрация: \( \displaystyle \frac{0,3}{4,8}=0,0625=6,25\%\).
Задача №11
Смешали два раствора: \( \displaystyle 2\) кг \( \displaystyle 10\%\)-ного и \( \displaystyle 3\) кг \( \displaystyle 20\%\)-ного. Какова концентрация полученного раствора?
Решение:
Визуализируем ситуацию: схематично изобразим емкости с растворами, около них подпишем массу раствора, а внутри – содержание кислоты:
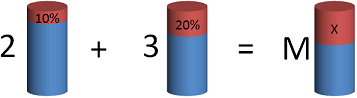
Теперь составляем два уравнения:
Задача №12
Изюм содержит \( \displaystyle 5\%\) влаги. Его получают из винограда, содержащего \( \displaystyle 90\%\) влаги. Сколько потребуется винограда, чтобы получить \( \displaystyle 3\) кг изюма?
Решение:
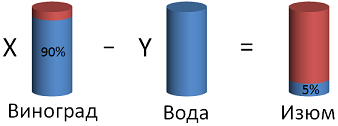
Получаем систему:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Нет. Спасибо.
Спасибо за объяснения! Все доступно изложено и структурированно по теории и практике. Наконец-то смогла разобраться с этой темой! Пойду решать задачи:)
Решать задачи — это самое правильное! Очень рады, что вы разобрались!
Некоторые комментарии прошлых лет к этой статье:
Ахтонг
19 октября 2017
я научился, хороший тест
Я
08 марта 2018
Спасибо, я благодаря вам поступлю в физ-мат:-) 🙂 🙂
Ксения
06 июня 2018
Такую простую вещь не могла долго понять, пока вы не объяснили доходчиво и доступно. Спасибо большое!
Наталья Викторовна.
27 августа 2019
Хорошая подборка заданий, говорю как учитель математики выпускных классов, Спасибо. До кого не доходит, отправлю к вам. Главное не останавливаться, если закрыт главный вход, попробуй зайти со служебного. Посмотрите второй пример, в тексте 3кг, на рис 5кг.