Физика — с чего начать
Знаешь, в чем проблема большинства людей?
В том, что, заметив что-то странное, они просто проходят мимо. И не пытаются разобраться.
Они живут, ходят на работу, где смотрят на горы документов, в школу, где смотрят на цифры на доске… Они укротители таблиц в Excel, повелители отчетов и цифр, номеров и отступов. И не задаются вопросами о том, как устроен мир.
Ты читаешь это, а значит, настал твой час встретиться с физикой. Возможно, ты хочешь научиться решать задачи. Или у тебя возникли трудности с какой-то темой.
Но я хочу показать тебе то, после чего ты поймешь, что физика – не просто формулы и вычисления. Не просто определения из учебника.
Ты научишься вещам, которые необходимы для того, чтобы изучать нашу Вселенную. Вещам, которые будут в том числе полезны (и просто необходимы!) для решения задач. И просто для жизни.
Сегодня ты узнаешь, как подготовиться к приключению длиной в жизнь, почему твой мозг не любит маленькие рисунки и как все прохожие на улице связаны между собой.
О рептилоидах, звездах и видеоиграх
Теоретически ты можешь нарушить закон, ты ведь свободен в своем выборе. Но не свободен от наказания 🙂
Есть законы, которые нарушить не удастся. И это законы физики.
Что, если я скажу тебе, что философия и физика не такие уж и разные? Они обе стараются объяснить законы нашей Вселенной, не так ли?
Наша Вселенная огромна. В ней множество удивительных явлений! Некоторые из них даже не удается объяснить. Пока что.
Но люди пытаются. И пытаются по-разному.
Из этого свободного пространства для мыслей возникают теории заговоров, гипотезы об НЛО…
И до многих людей доходит именно эта информация. Та, что так любят журналы и телевидение.
Из-за обилия подобной информации люди не видят, что настоящая наука может быть так же интересна, как и самая сумасшедшая, захватывающая история о рептилоидах (и даже более!)

Вот, например, одна из моих любимых цитат, которая это показывает:
За исключением водорода, все остальные атомы нашего тела – железо в крови, кальций в костях, углерод в мозгу – возникли в красных гигантах, в звездах, которых отделяют от нас тысячи световых лет в пространстве и миллиарды лет во времени. Мы состоим из вещества, из которого делаются звезды!
– Карл Саган
Физика везде. И она помогает людям не только в запуске космических спутников. Чтобы убедиться, хочу задать тебе вопрос…
Что делает игры реалистичными?
О, есть много вещей. Сюжет там, графика… Но даже самая качественная графика не сделает игру реалистичной без движения. На помощь приходит физика.
Она позволяет тебе наслаждаться анимацией травы, стрельбы, даже лицами героев!

Физика поможет тебе приготовить вкуснейшие блюда, победить на соревнованиях, найти путь, если ты заблудился… Ведь физика – наука красоты, правды и всеобщей связи.
Она очень обширна. Именно поэтому в ней есть огромное множество разделов и подразделов.
Вот основные из них:
Ты познакомишься с каждым. А сейчас мы научимся вещам, которые нужны для их освоения.
О метрах, секундах и канадском самолете
Однажды в 1983 году в канадский самолет залили 22 тысячи фунтов керосина вместо 22 тысяч килограмм.
Примерно в два раза меньше. На высоте 12 км оба двигателя перестали работать, а приборы отключились.

Самолет продолжал планировать в высоте, а командир Роберт Пирсон, проявив сообразительность, принял решение посадить его на старом военном аэродроме. Все пассажиры выжили.
К этой ситуации привела лишь одна ошибка – использование разных единиц измерения.
В физике мы работаем с единицами СИ. «СИ» есть «Система Интернациональная» («SI» = «Système International».) Для всех. Она нужна, чтобы не произошло ситуаций, подобных той, что описана выше.
Вот таблица с основными единицами СИ:
|
Величина |
Название |
Обозначение |
|
время |
секунда |
с |
|
длина |
метр |
м |
|
масса |
килограмм |
кг |
|
сила электрического тока |
Ампер |
А |
|
термодинамическая температура |
Кельвин |
К |
|
количество вещества |
моль |
моль |
|
сила света |
кандела |
кд |
Ты познакомишься с огромным множеством других величин, которые называются производными.
Почему они так называются? Потому что происходят от основных! Сейчас покажу.
Частота – еще одна физическая величина – измеряется в герцах (Гц). А знаешь, что такое герц? Это единица, деленная на секунду!
Любую производную величину можно представить с помощью основной.
Про это есть древний, написанный на скалах пещер анекдот о том, как Ньютон, Эйнштейн и Паскаль играли в прятки. Водить выпало Эйнштейну, Паскаль спрятался, а Ньютон просто продолжил стоять там же и начертил вокруг себя мелом квадрат метр на метр. Эйнштен его увидел и сказал: «Нашел Ньютона!», а Ньютон, хитро улыбнувшись, сказал: «Паскаля»
Ведь паскаль – единица измерения давления – есть ньютон, деленный на метр квадратный 🙂
Я еще расскажу тебе о разных приставках. Но об этом позже. А пока…
О буквах
В физике величины принято обозначать буквами. Зачастую эти буквы легко запомнить. Ведь большинство из них имеет «расшифровку».
Большинство сил в физике обозначается буквой \(F\), ведь слово «сила» в английском языке – «force» или «fortis» на латыни. Масса обозначается буквой \(m\) – «mass»
С другими величинами так же! \(A\) – работа. От немецкого «Arbeit». А высота \(h\) – «Höhe».

С другими величинами ты тоже познакомишься!
Некоторые можно понять, а некоторые простить просто запомнить 🙂
Например, магнитная индукция. Как думаешь, какая буква?
\(M\)? Или может \(I\)?
Довольно близко, мой друг. Это \(B\).
Кое-кто из ученых (о ком ты тоже узнаешь! 🙂 ) вообще не парился и просто назвал открытые величины буквами в алфавитном порядке. Как ты понял, индукция была в списке вторая.
А что делать, если забыл, какой буквой обозначить, например, длину или магнитную индукцию?
Послушай, физика – не телефонная книга, где рядом с каждой величиной стоит определенная (и только такая!) буква. Некоторые величины ты можешь обозначать сам. Только не забудь указать, что именно ты принял, например, за \(a\)
Предположим, я считаю силу Кулона.
Я знаю, что сила Кулона – перемножить заряды в модуле, постоянную и разделить на квадрат расстояния между зарядами.
Знаю, как обозначить все величины, кроме расстояния.
\( \displaystyle F=k\cdot \frac{\left| {{q}_{1}}\cdot {{q}_{2}} \right|}{{{?}^{2}}}\)Как быть?
Просто придумай обозначение! Но обязательно запиши, что это такое. Ты ведь не хочешь, чтобы людям было сложно разбираться в твоих трудах, верно?
Вот так:
\( \displaystyle F=k\cdot \frac{\left| {{q}_{1}}\cdot {{q}_{2}} \right|}{{{a}^{2}}}\), где \(a\) – расстояние между зарядами…
И т. д.
И ни у кого не возникнет вопросов!
(К слову, в действительности формула выглядит так: \( \displaystyle F=k\cdot \frac{\left| {{q}_{1}}\cdot {{q}_{2}} \right|}{{{r}^{2}}}\))
О математике и порядке в хаосе
Математика не только является лучшей подругой физики, но и сама по себе очень интересна. Эти науки очень похожи.
Математика, например, может доказать самые удивительные вещи.
Одна из ее теорий, теория Рамсея, доказывает то, что в любом хаосе ВСЕГДА найдется порядок. В звездах на небе, в прохожих на улице…
А, например, числа Фибоначчи помогают людям прогнозировать цены, писать картины и многое другое!
Математика помогает физике описывать мир в виде расчетов, формул, строгих правил. Давай попробуем с ней поработать.
Выражай и властвуй
Если не знаешь своей цели, то бродить будешь долго. Но даже если ты знаешь свою цель, тебе необходимо ее обозначить. Когда ты видишь свою цель впереди, идти становится намного легче.
К чему это я?
Дело в том, что в большинстве задач и расчётов твоей целью будет нахождение какой-либо величины. Это может быть ускорение свободного падения на Марсе, температура на Северном полюсе, количество молекул воды в твоем стакане… Все, что только захочешь узнать!
Считать будет намного легче, а ответы получатся намного точнее, если уметь выражать эти величины из полученных тобой формул.

Сейчас все разберем! Мы будем работать с дробями, корнями, суммой и разностью. И это реально все, что тебе нужно.
Я начну именно с дробей, потому что однажды узнал штуку, которая спасает меня до сих пор. Ты когда-нибудь задумывался, насколько число шесть классное? Нет, серьезно!
Если нет, то смотри сюда:
\(6=2\cdot 3\)Пока не удивлен, понимаю. Но эти три числа – твое спасение при работе с любыми дробями!
\( \displaystyle 2=\frac{6}{3}\)Сейчас объясню. Это выражение с дробью – что-то вроде упрощенной версии любой другой дроби, даже самой сложной.
Разберем на примере.
Вот формула давления:
\( \displaystyle P=\frac{F}{S}\)Давление есть сила, деленная на площадь поверхности.
Найдем площадь поверхности?
С буквами может показаться сложно. Но давай сопоставим с этой формулой наше любимое равенство!
\( \displaystyle P(2)=\frac{F(6)}{S(3)}\)Что нужно сделать, чтобы найти тройку?
Ты без труда ответишь, что нужно шесть разделить на два!
Так сделай это с соответствующими буквами!
Вот так:
\( \displaystyle S(3)=\frac{F(6)}{P(2)}\)Давай возьмем случай посложнее. Вот энергия конденсатора:
\( \displaystyle W=\frac{{{q}^{2}}}{2C}\)Квадрат заряда на удвоенную электроемкость.
Сначала попрошу найти электроемкость, а потом заряд 🙂
Возникает вопрос. Что делать с двойкой?
Здесь два пути. Либо представь, что \(2C\) – единое целое и работай так, же как выше…
\( \displaystyle 2C=\frac{{{q}^{2}}}{W}\)И затем дели обе части на двойку…
\( \displaystyle C=\frac{{{q}^{2}}}{2W}\)…либо пойми, что двойка – еще один множитель в формуле.
Стоп. Множитель? Она же в знаменателе!
И что?
А кто мешает записать так?
\( \displaystyle W=\frac{1}{2}\cdot \frac{{{q}^{2}}}{C}=\frac{\frac{1}{2}{{q}^{2}}}{C}\)В итоге, выражая емкость, получишь то же самое!
\( \displaystyle C=\frac{{{q}^{2}}}{2W}\)А теперь попробуем найти заряд.
Выражаем его:
\( \displaystyle W(2)=\frac{{{q}^{2}}(6)}{2C(3)}\)Получим:
\({{q}^{2}}=2CW\)Ведь шесть – это два умножить на три, верно?
Что ж, мы нашли квадрат заряда. Знаменатель.
Как найти просто заряд?
Взять все под корень! Но не забудь убедится, что не берешь под корень НЕОТРИЦАТЕЛЬНОЕ ЗНАЧЕНИЕ!
Если все выражаешь правильно, то так и получится.
То есть:
\( \displaystyle \sqrt{{{q}^{2}}}=\sqrt{2CW}\)Откуда: \(q=\sqrt{2CW}\)
А что делать, если то, что нужно выразить, находится под корнем?
Например, вот формула периода маятника:
\( \displaystyle T=2\pi \sqrt{\frac{l}{g}}\)Предположим, нужно найти \(l\) – длину нити. Что делать?
Сначала максимально обособим ее!
\( \displaystyle T=2\pi \frac{\sqrt{l}}{\sqrt{g}}=2\pi \frac{1}{\sqrt{g}}\cdot \sqrt{l}\)Теперь найти ее стало легче! Давай для удобства заменим все лишнее рядом с ней буквой \(a\):
\( \displaystyle T=\underbrace{2\pi \frac{1}{\sqrt{g}}}_{a}\cdot \sqrt{l}\)Теперь вообще легко. Помнишь, шесть есть два на три? 🙂
\(T=a\sqrt{l}\) \( \displaystyle l={{\left( \frac{T}{a} \right)}^{2}}\)Заменим букву:
\( \displaystyle l={{\left( \frac{T\sqrt{g}}{2\pi } \right)}^{2}}={{\left( \frac{T}{2\pi } \right)}^{2}}\cdot g\)Вот так 🙂
Еще одна полезная штука – пропорция. Это равенство отношений. Вот так:
\( \displaystyle \frac{a}{b}=\frac{c}{d}\)Давай попробуем избавиться от дробей.
Домножим сначала на \(b\), затем на \(d\)
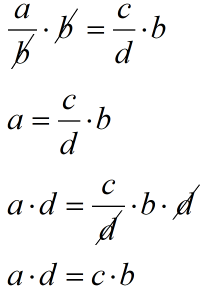
Это то, почему пропорция так полезна! Сформулируем.
Записав пропорцию, можешь перемножать крест-накрест:
\( \displaystyle \frac{a}{b}=\frac{c}{d}\Leftrightarrow a\cdot d=c\cdot b\)
Этот знак в середине показывает равносильность, одинаковость выражений.
Я думаю, что из математики ты уже знаешь, как переносить части выражений в разные стороны. А именно – с противоположным знаком.
Давай попробуем выразить из этой прекрасной формулы время \(t\):
\( \displaystyle V={{V}_{0}}+at\)Пытаемся обособить! Переносим.
Куда переносить? Что переносить?
Ну, на самом деле куда угодно. Сейчас покажу.
Ты можешь перенести часть с временем влево, а все остальное вправо. Учитывая знаки, получим:
\(-at={{V}_{0}}-V\)И тогда придется домножать обе части на \(-1\), чтобы избавиться от лишних минусов:
\(at=V-{{V}_{0}}\)(Ты ведь знаешь, что так можно делать? Ты можешь домножать/делить обе части выражения на одно число, прибавлять или отнимать одно и то же число, выражение от этого не изменится!)
Хотя ты просто мог перенести \({{V}_{0}}\) влево и получить сразу:
\(V-{{V}_{0}}=at\Leftrightarrow at=V-{{V}_{0}}\)Усвоил?
Попробуй сам!
Сверься с ответами:
Справился?
Я очень надеюсь, что ты не пытался решить их быстро и разбирался с каждым из заданий.
Если у тебя остались вопросы, напиши их в комментариях ниже. Мы во всем разберемся!
Это очень важно.
О том, почему важно совершать ошибки и как не совершить их в важный момент

Дело не в том, что я самый умный. Дело в том, что я уделяю решению проблем больше времени.
– Альберт Эйнштейн
Я знаю, что многие задачи по физике будут казаться тебе очень сложными. Возможно, это чувство останется даже после недель практики.
Но я хочу, чтобы ты знал: пока ты практикуешься и не сдаешься, ты движешься в правильном направлении. Даже если ты постоянно ошибаешься. И даже если целый час сидишь над задачей.
Избежать ошибок не получится никогда. И выбор того, что делать с ними, всегда за тобой.
Ты можешь просто бросить то, что ты делал, посчитав себя неудачником. А можешь взять от них все: опыт, знания…
И быть готовым к новому бою! 🙂
Чем больше ошибок ты совершишь сейчас, тем меньше их будет в важный момент. А если и будут, то ты знаешь, как их исправить.
Пока ты совершаешь ошибки, ты становишься сильнее, умнее… лучше. Как бы странно это ни звучало.
Знаешь, когда я слышу об ученых-физиках, я вспоминаю о художниках.
Они тоже описывают окружающий нас мир. Только, в отличие от физиков, их все понимают 🙂
Мне вспоминается цитата одного прекрасного человека, который был художником, Боба Росса. Она как раз о том, о чем шла речь выше.

Я надеюсь, что вы всю жизнь страдаете от неудовлетворенности. Потому что, если это так, вы всегда будете стремиться к лучшему.
– Боб Росс
Не бойся совершать ошибки. Горечь от них уйдет через месяц или даже неделю, а опыт останется с тобой навсегда.
Всегда помни, что порой очень полезно посмотреть на задачу с другой стороны, отложить ее на время и взглянуть на нее со свежей головой.
Может, попробовать другой путь.
Анализ размерности
Большинство ошибок можно избежать, совершив проверку. Давай посмотрим на один из самых полезных приемов, который поможет тебе убедиться в том, что твоя формула правильная.
Этот прием – анализ размерности.
Рассмотрим на простом примере. Вот две формулы из механики. Это формулы перемещения \(S\) и скорости \(V\).
\( \displaystyle S={{V}_{0}}t+\frac{a{{t}^{2}}}{2}\) \(V={{V}_{0}}+at\)Представим, что ты забыл какую-то формулу, но “примерно помнишь”, что там.
И ты пишешь:
\( \displaystyle V={{V}_{0}}+\frac{a{{t}^{2}}}{2}\)Но ты не уверен, так?
Остановись прямо здесь и выполни анализ размерности.
Запиши вместо величин единицы их измерения и посмотри, все ли сходится.
Например, ты знаешь, что скорость измеряется в метрах в секунду, вот и пиши:
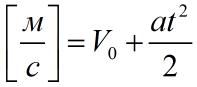
Время в секундах, а ускорение – в метрах в секунду в квадрате:
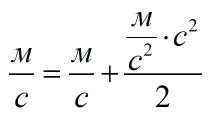
Теперь сокращай все, что можешь:
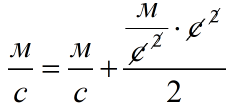
Cмотри, что получилось:
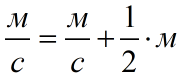
Обрати внимание на единицы измерения, на числа внимания особого не обращай.
Что видишь?
Тебе нужно получить метры в секунду. А ты прибавляешь к метрам в секунду (\({{V}_{0}}\)) просто метры (\( \displaystyle \frac{a{{t}^{2}}}{2}\))! Конечно, так метры в секунду не получишь.
Не можешь прибавить доллары к пончикам 🙂
Значит, в формуле есть какая-то ошибка.
И ошибка в части \( \displaystyle \frac{a{{t}^{2}}}{2}\), ведь в этой части нам нужно тоже получить метры в секунду.
Давай посмотрим на правильную формулу в анализе размерностей:
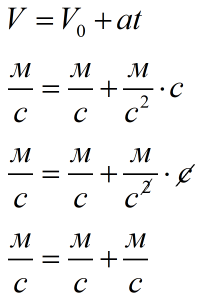
Все сходится!
Это очень полезный прием. Он работает всегда и спасет тебя, когда ты не уверен в правильности своих формул.
О степенях и приставках
В физике нет хороших чисел.
Так уж получилось, она ведь описывает реальность.
Существуют огромные числа. Существуют очень маленькие. Настолько маленькие, что ты замучаешься писать нули после запятой! А тем более считать их.
Например, вот сколько времени ушло на то, чтобы наша Вселенная начала формироваться:
\(0,0000000000000000000000000000000000000000001\)с
Выглядит устрашающе.
А еще страшнее название этого числа, если попробовать назвать его по аналогии с одной десятой или двумя тысячными, верно?
Можно записать проще:
\( \displaystyle {{10}^{-43}}\)с
Выглядит красивее, правда? И читать проще: «десять в минус сорок третьей секунд»
Вычисления с таким количеством нулей сложно провести даже на калькуляторе. Поэтому очень важно научиться работать со степенями десятки.
Нужно помнить несколько простых фактов.
\( \displaystyle \frac{5\cdot {{10}^{-4}}}{3}=\frac{5}{3\cdot {{10}^{4}}}\) \( \displaystyle \frac{6}{7\cdot {{10}^{-8}}}=\frac{6\cdot {{10}^{8}}}{7}\)Иными словами, сколько раз нужно перенести запятую влево, вот так:
\( \displaystyle 33\cdot {{10}^{-6}}=0,\underset{\scriptscriptstyle\leftarrow}{0}\underset{\scriptscriptstyle\leftarrow}{0}\underset{\scriptscriptstyle\leftarrow}{0}\underset{\scriptscriptstyle\leftarrow}{0}\underset{\scriptscriptstyle\leftarrow}{3}\underset{\scriptscriptstyle\leftarrow}{3}\)Видишь, шесть стрелочек (шесть перемещений запятой) с конца числа \(33\).
\( \displaystyle 0,\underbrace{0}_{1}\underbrace{0}_{2}\underbrace{8}_{3}\underbrace{4}_{4}=84\cdot {{10}^{-4}}\)\( \displaystyle 16\cdot {{10}^{2}}=1600\)
\( \displaystyle 0,21\cdot {{10}^{5}}=21000\)
Иными словами, сколько раз нужно подвинуть запятую вправо:
Пять стрелочек, десять в пятой степени.
В системе СИ (опять она!) некоторые степени десятки имеют свои собственные названия-приставки. Я покажу тебе главные. Если интересно, другие сможешь найти сам (что я очень советую сделать!).
Смотри таблицы и читай объяснение!
Для кратных единиц (тех, которые умножают на десятку)
|
Множитель (десятка в степени) |
Название приставки |
Обозначение |
Пример |
|
\( displaystyle {{10}^{3}}\) |
кило |
к |
км – километр |
|
\( displaystyle {{10}^{6}}\) |
мега |
М |
МКл – мегакулон |
|
\( displaystyle {{10}^{9}}\) |
гига |
Г |
ГГц – гигагерц |
|
\( displaystyle {{10}^{12}}\) |
тера |
Т |
ТПа – терапаскаль |
Для дольных единиц (тех, которые делят)
|
Множитель (десятка в степени) |
Название приставки |
Обозначение |
Пример |
|
\( displaystyle {{10}^{-3}}\) |
милли |
м |
мА – миллиампер |
|
\( displaystyle {{10}^{-6}}\) |
микро |
мк |
мкФ – микрофарад |
|
\( displaystyle {{10}^{-9}}\) |
нано |
н |
нм – нанометр |
|
\( displaystyle {{10}^{-12}}\) |
пико |
п |
пс – пикосекунда |
Сейчас объясню, как этими штуками пользоваться.
Например, ты считал длину какой-то частицы. Посчитал ее в метрах, вот она:
\(0,000009\)м
Выделил десятку со степенью:
\( \displaystyle 0,000009=9\cdot {{10}^{-6}}\)м
Чтобы не таскать за собой десятку, ты можешь просто записать ее в виде приставки к единицам измерения.
Смотрим в таблице: \( \displaystyle {{10}^{-6}}\) – это микро (мк). Единицы измерения – метры. Значит пишем:
\(9\)мкм, что значит \(9\) микрометров! Вот и все!
Кстати, именно из-за приставок в килограмме тысяча (\( \displaystyle {{10}^{3}}\)) грамм 🙂
Будь очень внимателен с заглавными и строчными буквами.
Большая разница, если тронуть провод напряжением 5 милливольт (мВ) или 5 мегавольт (МВ), правда? Не трогай провода! 🙂
Давай попробуем решить пример, который проиллюстрирует все сказанное выше.
Посчитать и записать ответ так, чтобы запятой в нем не было:
\( \displaystyle \frac{5\cdot {{10}^{-8}}}{2\cdot {{10}^{-6}}}\)м
Итак, сначала разберемся со степенями десятки. Переносим их, меняя знак степени:
\( \displaystyle \frac{5\cdot {{10}^{6}}}{2\cdot {{10}^{8}}}\)Далее сокращаем их. Получим:
\( \displaystyle \frac{5}{2}\cdot \frac{{{10}^{6}}}{{{10}^{8}}}=\frac{5}{2}\cdot {{10}^{-2}}=2,5\cdot {{10}^{-2}}\)м
Нам нужно записать ответ без запятой. Это случится, если мы с помощью степеней десятки получим \(25\).
Давай подумаем.
Это случится, если мы домножим \(2,5\) на десять, верно?
Но тогда, чтобы сохранить равенство, нам нужно и разделить на десять!
Можно сказать, что \( \displaystyle 2,5=25:10=25\cdot {{10}^{-1}}\).
Запишем в нашем случае:
\( \displaystyle \underbrace{2,5}_{25\cdot {{10}^{-1}}}\cdot {{10}^{-2}}=25\cdot {{10}^{-3}}\)м
А что мы помним про эту степень десятки? Она заменяется приставкой!
И мы получим \(25\)мм (миллиметров)
Продолжай практиковаться и станешь рациональнее калькулятора! 🙂
О чистых черновиках, микроскопических рисунках и лабиринтах нашего разума
Я знаю много людей, которые, видя сложную задачу, просто тяжко вздыхают и смотрят на пустые листы перед собой.
А еще я знаю тех, кто »жалеет бумагу».
Не подумай, что я ненавистник деревьев, вовсе нет! Я просто знаю, насколько важно отражать свои мысли на бумаге. Да и вообще где тебе удобно.
Даже если задача кажется невероятно сложной, ты в любом случае можешь определить ее тему, так? Например, смотришь и думаешь: «Ну, это задача на движение…»
Что ж, если ты определил тему этой задачи, ты уже знаешь, откуда дует ветер. Пиши формулы! Пиши свои мысли, пиши все, что знаешь. Возможно, тебе это очень поможет.
Визуально информация воспринимается намного лучше. Когда видишь перед собой формулы, можешь заметить связь между ними или разные способы нахождения той или иной величины!
Представь двух людей, которые ходят в лабиринте. У одного из них есть лист бумаги и карандаш. Как думаешь, кто будет часто заходить в одни и те же тупики?
Тот, у кого бумаги нет. Он не сможет как-то записать свои наблюдения, не сможет попытаться составить карту и увидеть картину в целом.
С черновиками так же.
Иногда твои черновики будут похожи на записки сумасшедшего. Так бывает, когда ты очень стараешься! 🙂
Не пугайся и не забывай как-то выделять особо важные моменты и ответы.
Я хочу отдельно поговорить о рисунках. И единственное, что я хочу сказать… Пожалуйста, не заставляй меня доставать микроскоп!
И это вовсе не потому, что я так трепетно отношусь к своему зрению. Все дело в тебе.
Крупные рисунки помогут тебе поместить в них больше полезной информации. Когда подписи и части рисунка лезут друг на друга, любая информация, которую они несут, утрачивает свою ценность.
Тебе будет сложно всматриваться в них. Твой мозг будет концентрироваться на том, как разделить эти мелкие штрихи, будет сложнее думать о самой задаче, даже если ты этого не осознаешь.
Рисунок хорошего размера поможет тебе. Маленького – будет мешать.
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Как приятно видеть то, что ты каждый день пытаешься донести до учеников словами, в тексте! Это так просто и так сложно оформить это письменно! Благодарю вас, я в восторге!
Спасибо большое, Анастасия за такой отзыв! Удачи вам и вашим ученикам!
Шикарно!
Наконец-то пойму физику!!! Ощущение, что в моих руках вся власть этой Вселенной! По этим статьям, кстати, можно юных философов учить))
Спасибо, Юный физик! Обязательно поймешь! Очень приятно видеть тебя в статьях по физике после статей по математике 🙂 Ты права, власть и правда в твоих руках!
Прекрасные объяснения, замечательные гифки! Спасибо за Ваш труд, Александра! Всегда приятно воспринимать информацию в такой форме!
Спасибо! Как приятно получать от Вас фидбэк! Ваш комментарий очень меня вдохновил!