Замена переменных в уравнениях
Метод замены переменных… Что это за зверь?
Это хитрый способ сначала сделать сложное уравнение простым (с помощью замены переменных) и потом быстро с ним разделаться.
Есть три способа замены переменной.
Читай эту статью — ты все поймешь!
Замена переменных — коротко о главном
Определение:
Замена переменных – метод решения сложных уравнений и неравенств, который позволяет упростить исходное выражение и привести его к стандартному виду.
Замена переменных – это введение нового неизвестного, относительно которого уравнение или неравенство имеет более простой вид.
Виды замены переменной:
Степенная замена: за \( \displaystyle t\) принимается какое-то неизвестное, возведенное в степень: \( \displaystyle t={{x}^{n}}\).
Дробно-рациональная замена: за \( \displaystyle t\) принимается какое-либо отношение, содержащее неизвестную переменную: \( \displaystyle t=\frac{{{P}_{n}}\left( x \right)}{{{Q}_{m}}\left( x \right)}\), где \( \displaystyle {{P}_{n}}\left( x \right)\) и \( \displaystyle {{Q}_{m}}\left( x \right)~\) – многочлены степеней n и m, соответственно.
Замена многочлена: за \( \displaystyle t\) принимается целое выражение, содержащее неизвестное: \( \displaystyle t={{P}_{n}}\left( x \right)\) или \( \displaystyle t=\sqrt{{{P}_{n}}\left( x \right)}\), где \( \displaystyle {{P}_{n}}\left( x \right)~\) – многочлен степени \( \displaystyle n\).
Обратная замена:
После решения упрощенного уравнения/неравенства, необходимо произвести обратную замену.
Степенная замена \( \displaystyle y={{x}^{n}}\)
Решение примера №1
Допустим, у нас есть выражение: \( \displaystyle {{x}^{4}}-5{{x}^{2}}-36=0\).
Подумай, к какому виду мы можем его привести, чтобы при расчетах легко найти корни? Правильно, данное уравнение необходимо привести к квадратному виду.
Введем новую переменную \( \displaystyle t={{x}^{2}}\).
Метод замены переменной подразумевает, чтобы старой переменной \( \displaystyle x\) не оставалось – в выражении должна остаться только одна переменная – \( \displaystyle t\).
Наше выражение приобретет вид:
\( \displaystyle {{t}^{2}}-5t-36=0\) – обычное квадратное уравнение
\( \displaystyle \text{D}={{\text{b}}^{2}}-4\text{ac}\) \( \displaystyle \text{D}=25-4\cdot 1\cdot \left( -36 \right)=25+144=169\) \( \displaystyle \sqrt{\text{D}}=\sqrt{169}=13\) \( \displaystyle {{t}_{1,2}}=\frac{-b\pm \sqrt{D}}{2a}\) \( \displaystyle {{t}_{1}}=\frac{5+13}{2}=9\) \( \displaystyle {{t}_{2}}=\frac{5-13}{2}=-4\)Нашли ли мы корни исходного уравнения? Правильно, нет.
На этом шаге не следует забывать, что нам необходимо найти значения переменной \( \displaystyle x\), а мы нашли только \( \displaystyle t\).
Следовательно, нам необходимо вернуться к исходному выражению, то есть сделать обратную замену — вместо \( \displaystyle t\) ставим \( \displaystyle {{x}^{2}}\).
Далее найдем
\( \displaystyle {{x}^{2}}=9\) \( \displaystyle {{x}^{2}}=-4\)Решаем два новых простых уравнения, не забывая область допустимых значений!
Три основных правила замены переменных:
- Замену переменных нужно делать сразу и при первой же возможности.
- Уравнение (неравенство) относительно новой переменной необходимо решать до конца, и лишь затем возвращаться к старому неизвестному.
- При возврате к изначальному неизвестному (да и вообще на протяжении всего решения), не забывай проверять корни на ОДЗ.
Решение примера №2
Попробуй самостоятельно применить метод замены переменной в уравнении \( \displaystyle 3{{x}^{6}}-7{{x}^{3}}+2=0\).
Подумай, к какому виду мы можем его привести, чтобы при расчетах легко найти корни?
Проверь свое решение:
Введем новую переменную \( \displaystyle t={{x}^{3}}\).
Наше выражение приобретет вид:
\( \displaystyle 3{{t}^{2}}-7t+2=0\) – обычное квадратное уравнение
\( \displaystyle \text{D}={{\text{b}}^{2}}-4\text{ac}\) \( \displaystyle \text{D}=49-4\cdot 3\cdot 2=49-24=25\) \( \displaystyle \sqrt{\text{D}}=\sqrt{25}=5\) \( \displaystyle {{t}_{1,2}}=\frac{-b\pm \sqrt{D}}{2a}\) \( \displaystyle {{t}_{1}}=\frac{7+5}{6}=2\) \( \displaystyle {{t}_{2}}=\frac{7-5}{6}=\frac{2}{6}=\frac{1}{3}\)Возвращаемся к исходному выражению, то есть делаем обратную замену:
Степенная замена в общем виде
\( \displaystyle y={{x}^{n}}\)
Например, с помощью замены \( \displaystyle t={{x}^{2}}\) биквадратное уравнение \( \displaystyle a{{x}^{4}}+b{{x}^{2}}+c=0,\text{ }a\ne 0\) приводится к квадратному: \( \displaystyle a{{t}^{2}}+bt+c=0\).
В неравенствах все аналогично.
Например, в неравенстве \( \displaystyle a{{x}^{6}}+b{{x}^{3}}+c\ge \text{0}\) сделаем замену \( \displaystyle t={{x}^{3}}\), и получим квадратное неравенство: \( \displaystyle a{{t}^{2}}+bt+c\ge \text{0}\).
Дробно-рациональная замена
Дробно-рациональная замена – \( \displaystyle y=\frac{{{P}_{n}}\left( x \right)}{{{Q}_{m}}\left( x \right)},~{{P}_{n}}\left( x \right)~и~{{Q}_{m}}\left( x \right)~\) многочлены степеней n и m соответственно.
При этом необходимо помнить, что область допустимых значений (ОДЗ) данного уравнения \( \displaystyle {{Q}_{m}}\left( x \right)\ne 0\) (так как на ноль делить нельзя).
Решение примера №3
Допустим, у нас есть уравнение:
\( \displaystyle {{x}^{2}}+\frac{9}{{{x}^{2}}}-{x}-\frac{3}{x}=14\)Так как на ноль делить нельзя, то в данном случае ОДЗ будет: \( \displaystyle x\ne 0\)
Сгруппируем слагаемые:
\( \displaystyle \left( {{x}^{2}}+\frac{9}{{{x}^{2}}} \right)-\left( x+\frac{3}{x} \right)-14=0\)Введем новую переменную \( \displaystyle t\).
Пусть \( \displaystyle t=x+\frac{3}{x}\), тогда
\( \displaystyle {{t}^{2}}={{\left( x+\frac{3}{x} \right)}^{2}}={{x}^{2}}+\frac{9}{{{x}^{2}}}+2x\cdot \frac{3}{x}\)Сравни, что дает возведение \( \displaystyle t\) в квадрат, с первой сгруппированной скобкой в нашем примере. Что ты видишь?
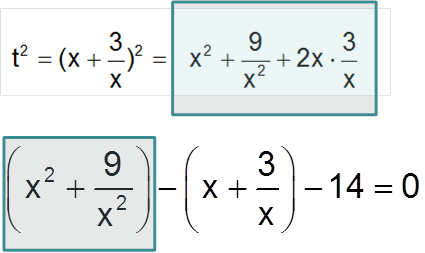
Правильно. Разница между тем, что у нас в примере, и тем, что дает нам возведение в квадрат, заключается в удвоенном произведении слагаемых.
Соответственно, его и следует вычесть, переписывая наш пример с переменной \( \displaystyle t\).
\( \displaystyle 2{x}\cdot \frac{3}{{x}}=6\)В итоге мы получаем следующее выражение:
\( \displaystyle {{t}^{2}}-6-t-14=0\) – обычное квадратное уравнение.
Решаем получившееся уравнение:
\( \displaystyle {{\text{t}}^{2}}-\text{t}-20=0\) \( \displaystyle \text{D}={{\text{b}}^{2}}-4\text{ac}\) \( \text{D}=1-4\cdot \left( -20 \right)=1+80=81\) \( \sqrt{\text{D}}=\sqrt{81}=9\) \( {{t}_{1,2}}=\frac{-b\pm \sqrt{D}}{2a}\) \( {{t}_{1}}=\frac{1+9}{2}=5\) \( {{t}_{2}}=\frac{1-9}{2}=\frac{-8}{2}=-4\)Как мы помним \( t\), не является конечным решением уравнения. Возвращаемся к изначальной переменной:
\( \displaystyle \left[ \begin{array}{l}x+\frac{3}{x}=5;\\x+\frac{3}{x}=-4.\end{array} \right.\)Приводя к общему знаменателю \( \displaystyle x\), мы приходим к совокупности 2-x квадратных уравнений:
\( \displaystyle \left[ \begin{array}{l}{{x}^{2}}-5x+3=0;\\{{x}^{2}}+4x+3=0.\end{array} \right.\)Решим первое квадратное уравнение:
Решение пример №4
\( \displaystyle \frac{5}{{{\left( {x}-2 \right)}^{2}}}-{{\left( {x}-2 \right)}^{2}}-4=0\)Какой ответ у тебя получился? У меня \( \displaystyle 1\) и \( \displaystyle 3\).
Сравним ход решения:
Пусть \( \displaystyle t=\frac{1}{{{\left( {x}-2 \right)}^{2}}}\), тогда выражение приобретает вид:
\( \displaystyle 5t-\frac{1}{{t}}-4=0\)Приведем слагаемые к общему знаменателю:
\( \displaystyle \frac{5{{\text{t}}^{2}}-4\text{t}-1}{\text{t}}=0\)Не забываем про ОДЗ — \( \displaystyle t\ne 0\)!!!!!
Решаем квадратное уравнение:
\( \displaystyle 5{{\text{t}}^{2}}-4\text{t}-1=0\) \( \displaystyle \text{D}={{\text{b}}^{2}}-4\text{ac}\) \( \displaystyle \text{D}=16-4\cdot 5\cdot \left( -1 \right)=16+20=36\) \( \displaystyle \sqrt{\text{D}}=\sqrt{36}=6\) \( \displaystyle {{t}_{1,2}}=\frac{-\text{b}\pm \sqrt{\text{D}}}{2\text{a}}\) \( \displaystyle {{\text{t}}_{1,2}}=\frac{4\pm 6}{2\cdot 5}\) \( \displaystyle {{\text{t}}_{1}}=\frac{4+6}{10}=1\) \( \displaystyle {{\text{t}}_{2}}=\frac{4-6}{10}=-\frac{2}{10}=-\frac{1}{5}\)Как ты помнишь, \( \displaystyle t\) не является конечным решением уравнения. Возвращаемся к изначальной переменной:
Дробно-рациональная замена в общем виде
\( \displaystyle t=\frac{{{P}_{n}}\left( x \right)}{{{Q}_{m}}\left( x \right)}\)
\( \displaystyle {{P}_{n}}\left( x \right)\) и \( \displaystyle {{Q}_{m}}\left( x \right)\) − многочлены степеней \( \displaystyle n\) и \( \displaystyle m\) соответственно.
Например, при решении возвратных уравнений, то есть уравнений вида
\( \displaystyle a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+bx+a=0,\text{ }a\ne 0\),
обычно используется замена \( \displaystyle t=x+\frac{1}{x}\).
Сейчас покажу, как это работает.
Легко проверить, что \( \displaystyle x=0\) не является корнем этого уравнения: ведь если подставить \( \displaystyle x=0\) в уравнение, получим \( \displaystyle a=0\), что противоречит условию.
Разделим уравнение на \( \displaystyle {{x}^{2}}\ne 0\):
\( \displaystyle a{{x}^{2}}+bx+c+\frac{b}{x}+\frac{a}{{{x}^{2}}}=0\).
Перегруппируем:
\( \displaystyle a\left( {{x}^{2}}+\frac{1}{{{x}^{2}}} \right)+b\left( x+\frac{1}{x} \right)+c=0\).
Теперь делаем замену: \( \displaystyle t=x+\frac{1}{x}\).
Прелесть ее в том, что при возведении в квадрат в удвоенном произведении слагаемых сокращается x:
\( \displaystyle {{t}^{2}}={{\left( x+\frac{1}{x} \right)}^{2}}={{x}^{2}}+2\cdot x\cdot \frac{1}{x}+\frac{1}{{{x}^{2}}}={{x}^{2}}+\frac{1}{{{x}^{2}}}+2\)
Отсюда следует, что \( \displaystyle {{x}^{2}}+\frac{1}{{{x}^{2}}}={{\left( x+\frac{1}{x} \right)}^{2}}-2={{t}^{2}}-2\).
Вернемся к нашему уравнению:
\( \displaystyle \begin{array}{l}a\left( {{x}^{2}}+\frac{1}{{{x}^{2}}} \right)+b\left( x+\frac{1}{x} \right)+c=0\text{ }\Leftrightarrow \text{ }a\left( {{t}^{2}}-2 \right)+bt+c=0\text{ }\Leftrightarrow \\a{{t}^{2}}+bt+c-2a=0\end{array}\)
Теперь достаточно решить квадратное уравнение и сделать обратную замену.
Замена многочлена
Замена многочлена \( \displaystyle y={{P}_{n}}\left( x \right)\) или \( \displaystyle y=\sqrt{{{P}_{n}}\left( x \right)}\).
Здесь \( \displaystyle {{P}_{n}}\left( x \right)~\) — многочлена степени \( \displaystyle n\), например, выражение \( \displaystyle 12{{x}^{3}}+2{{x}^{2}}-3x+1\) – многочлен степени \( \displaystyle 3\).
Решение примера №4
\( \displaystyle \left( {{{x}}^{2}}-4{x}+3 \right)\left( {{{x}}^{2}}-4{x}+4 \right)=20\)Применим метод замены переменной. Как ты думаешь, что нужно принять за \( \displaystyle t\)?
Правильно, \( \displaystyle t={{{x}}^{2}}-4{x}+3\).
Уравнение приобретает вид:
\( \displaystyle {t}\cdot \left( {t}+1 \right)=20\) \( \displaystyle {{{t}}^{2}}+{t}-20=0\) \( \displaystyle \text{D}={{{b}}^{2}}-4{ac}\) \( \displaystyle \text{D}=1-4\cdot \left( -20 \right)=1+80=81\) \( \displaystyle \sqrt{\text{D}}=\sqrt{81}=9\) \( \displaystyle {{t}_{1,2}}=\frac{-\text{b}\pm \sqrt{\text{D}}}{2\text{a}}\) \( \displaystyle {{{t}}_{1,2}}=\frac{-1\pm 9}{2}\) \( \displaystyle {{{t}}_{1}}=\frac{-1+9}{2}=4\) \( \displaystyle {{{t}}_{2}}=\frac{-1-9}{2}=-5\)Производим обратную замену переменных:
Решение примера №5
\( \displaystyle \left( 2{{{x}}^{2}}-9{x}+5 \right)\left( 2{{{x}}^{2}}-9{x}+6 \right)=2\)Решил? Теперь проверим с тобой основные моменты.
За \( \displaystyle t\) нужно взять \( \displaystyle 2{{{x}}^{2}}-9{x}+5\).
Мы получаем выражение:
\( \displaystyle \text{t}\cdot \left( \text{t}+1 \right)=2\)Решая квадратное уравнение, мы получаем, что \( t\) имеет два корня: \( \displaystyle -2\) и \( \displaystyle 1\).
Далее делаем обратную замену и решаем оба квадратных уравнения.
Решением первого квадратного уравнения являются числа \( \displaystyle 1\) и \( \displaystyle 3,5\)
Решением второго квадратного уравнения — числа \( \displaystyle 0,5\) и \( \displaystyle 4\).
Ответ: \( \displaystyle 0,5\); \( \displaystyle 1\); \( \displaystyle 3,5\); \( \displaystyle 4\)
Замена многочлена в общем виде
\( \displaystyle t={{P}_{n}}\left( x \right)\) или \( \displaystyle t=\sqrt{{{P}_{n}}\left( x \right)}\).
Здесь \( \displaystyle {{P}_{n}}\left( x \right)\) − многочлен степени \( \displaystyle n\), т.е. выражение вида
\( \displaystyle {{P}_{n}}\left( x \right)={{a}_{0}}{{x}^{n}}+{{a}_{1}}{{x}^{n-1}}+{{a}_{2}}{{x}^{n-2}}+…+{{a}_{n-1}}x+{{a}_{n}},\text{ }{{a}_{0}}\ne 0\)(например, выражение \( \displaystyle 4{{x}^{4}}+2{{x}^{3}}-3x+1\) – многочлен степени \( \displaystyle 4\), то есть \( \displaystyle {{P}_{4}}\left( x \right)\)).
Чаще всего используется замена квадратного трехчлена: \( \displaystyle t=a{{x}^{2}}+bx+c\) или \( \displaystyle t=\sqrt{a{{x}^{2}}+bx+c}\).
Подведем итоги
Метод замены переменной имеет \( \displaystyle 3\) основных типа замен переменных в уравнениях и неравенствах:
Степенная замена, когда за \( \displaystyle t\) мы принимаем какое-то неизвестное, возведенное в степень.
Замена многочлена, когда за \( \displaystyle t\) мы принимаем целое выражение, содержащее неизвестное.
Дробно-рациональная замена, когда за \( \displaystyle t\) мы принимаем какое-либо отношение, содержащее неизвестную переменную.
Важные советы при введении новой переменной
- Замену переменных нужно делать сразу и при первой же возможности.
- Уравнение (неравенство) относительно новой переменной необходимо решать до конца, и лишь затем возвращаться к старому неизвестному.
- При возврате к изначальному неизвестному (да и вообще на протяжении всего решения), не забывай проверять корни на ОДЗ.
- Новая переменная вводится аналогичным образом, как в уравнениях, так и в неравенствах.
Разбор 3 примеров на замену переменных
Пример 6. \( \displaystyle {{{x}}^{6}}+7{{{x}}^{3}}-8=0\)
Пример 7. \( \displaystyle \left( {{{x}}^{2}}-4{x}+7 \right)\left( {{{x}}^{2}}-4{x}+6 \right)=12\)
Пример 8. \( \displaystyle {{x}^{2}}+\frac{16}{{{x}^{2}}}-{x}-\frac{4}{x}=12\)
Решение примера №6
Пусть \( \displaystyle \text{t}={{{x}}^{3}}\), тогда выражение приобретает вид \( \displaystyle {{t}^{2}}+7\text{t}-8=0\).
Так как \( \displaystyle \text{t}={{{x}}^{3}}\), то может быть как положительным, так и отрицательным.
\( \displaystyle {{\text{t}}_{1}}=1\), \( \displaystyle {{\text{t}}_{2}}=-8\)
\( \displaystyle {{x}_{1}}=1\), \( \displaystyle {{{x}}_{2}}=-2\)
Ответ: \( \displaystyle -2;\text{ }1\)
Решение примера №7
Пусть \( \displaystyle \text{t}={{{x}}^{2}}-4{x}+7\), тогда выражение приобретает вид \( \displaystyle \text{t}\cdot \left( \text{t}-1 \right)=12\).
\( \displaystyle {{\text{t}}_{1}}=4\Rightarrow {{x}_{1}}=1;~~~~{{x}_{2}}=3.\)
\( \displaystyle {{\text{t}}_{2}}=-3\Rightarrow \) решения нет, так как \( \displaystyle D<0\).
Ответ: \( \displaystyle 1;3\)
Решение примера №8
Группировкой получаем:
\( \displaystyle \left( {{x}^{2}}+\frac{16}{{{x}^{2}}} \right)-\left( x+\frac{4}{x} \right)-12=0\)
Пусть \( \displaystyle \text{t}=x+\frac{4}{x}\), тогда выражение приобретает вид
\( \displaystyle {{\text{t}}^{2}}-\text{t}-8-12=0\Rightarrow {{t}^{2}}-t-20=0.\)
\( \displaystyle {{\text{t}}_{1}}=5\Rightarrow {{x}_{1}}=1;~~~~{{x}_{2}}=4.\)
\( \displaystyle {{\text{t}}_{2}}=-4\Rightarrow {{x}_{1}}=-2\)
Ответ: \( \displaystyle -2;\text{ }1;\text{ }4.\)
Тренировка решения более сложных задач
Решение примера №9 (степенная замена)
\( \displaystyle \frac{2+{{x}^{3}}}{{{x}^{6}}+6}=\frac{3}{2{{x}^{3}}+3}\)Решение:
Это дробно-рациональное уравнение (повтори «Рациональные уравнения»), но решать его обычным методом (приведение к общему знаменателю) неудобно, так как мы получим уравнение \( \displaystyle 6\) степени, поэтому применяется замена переменных.
Все станет намного проще после замены:
Решение примера 10 (замена многочлена)
Решите уравнение \( \displaystyle \left( {{x}^{2}}+5x+9 \right)\left( {{x}^{2}}+5x+10 \right)=12\).
Решение:
И опять используется замена переменных \( \displaystyle t={{x}^{2}}+5x+9\). Тогда уравнение примет вид:
\( \displaystyle t\cdot \left( t+1 \right)=12\text{ }\Rightarrow \text{ }{{t}^{2}}+t-12=0\).
Корни этого квадратного уравнения: \( \displaystyle t=-4\) и \( \displaystyle t=3\). Имеем два случая. Сделаем обратную замену для каждого из них:
Решение пример №11 (дробно-рациональная замена)
Решите уравнение: \( \displaystyle {{x}^{4}}-7{{x}^{3}}+14{{x}^{2}}-7x+1=0\).
Решение:
При \( \displaystyle x=0\) равенство не выполняется, поэтому \( \displaystyle x\ne 0\). Разделим уравнение на \( \displaystyle {{x}^{2}}\ne 0\):
\( \displaystyle {{x}^{4}}-7{{x}^{3}}+14{{x}^{2}}-7x+1=0\text{ }\left| :{{x}^{2}}\ne 0 \right.\text{ }\Leftrightarrow \)
\( \displaystyle {{x}^{2}}-7x+14-\frac{7}{x}+\frac{1}{{{x}^{2}}}=0\text{ }\Leftrightarrow \text{ }\)
\( \displaystyle \left( {{x}^{2}}+\frac{1}{{{x}^{2}}} \right)-7\left( x+\frac{1}{x} \right)+14=0\)
Замена: \( \displaystyle t=x+\frac{1}{x}\).
Тогда \( \displaystyle {{t}^{2}}={{\left( x+\frac{1}{x} \right)}^{2}}={{x}^{2}}+2\cdot x\cdot \frac{1}{x}+\frac{1}{{{x}^{2}}}={{x}^{2}}+\frac{1}{{{x}^{2}}}+2\text{ }\Rightarrow \text{ }\left( {{x}^{2}}+\frac{1}{{{x}^{2}}} \right)={{t}^{2}}-2\).
Уравнение примет вид:
\( \displaystyle {{t}^{2}}-2-7t+14=0\text{ }\Leftrightarrow \text{ }{{t}^{2}}-7t+12=0\).
Его корни: \( \displaystyle \left[ \begin{array}{l}t=3\\t=4\end{array} \right.\)
Произведем обратную замену:
Решение примера №12 (Дробно-рациональная замена)
Решите неравенство \( \displaystyle \frac{12x}{4{{x}^{2}}-8x+7}+\frac{13x}{4{{x}^{2}}-10x+7}\le -1\).
Решение:
Непосредственной подстановкой убеждаемся, что \( \displaystyle x\text{ }=\text{ }0\) не входит в решение этого неравенства. Разделим числитель и знаменатель каждой из дробей на \( \displaystyle x\text{ }\ne \text{ }0\):
\( \displaystyle \frac{12x}{4{{x}^{2}}-8x+7}+\frac{13x}{4{{x}^{2}}-10x+7}\le -1\text{ }\Leftrightarrow \text{ }\frac{12}{4{x}-8+\frac{7}{x}}+\frac{13}{4{x}-10+\frac{7}{x}}\le -1\).
Теперь очевидна замена переменной: \( \displaystyle y=4x+\frac{7}{x}\).
Тогда неравенство примет вид
\( \displaystyle \begin{array}{l}\frac{12}{y-8}+\frac{13}{y-10}\le -1\text{ }\Leftrightarrow \text{ }\frac{12y-120+13y-104+\left( y-8 \right)\left( y-10 \right)}{\left( y-8 \right)\left( y-10 \right)}\le 0\text{ }\Leftrightarrow \text{ }\frac{{{y}^{2}}+7y-144}{\left( y-8 \right)\left( y-10 \right)}\le 0\text{ }\Leftrightarrow \text{ }\frac{\left( y-9 \right)\left( y+16 \right)}{\left( y-8 \right)\left( y-10 \right)}\le 0\end{array}\)
Используем метод интервалов для нахождения y:
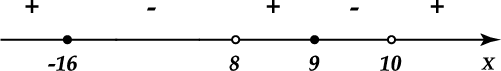
\( \displaystyle y\ge -16\Rightarrow 4x+\frac{7}{x}\ge -16\Rightarrow \frac{4{{x}^{2}}+16x+7}{x}\ge 0\Rightarrow \frac{4\left( x+\frac{1}{2} \right)\left( x+\frac{7}{2} \right)}{x}\ge 0\).

\( \displaystyle x\in \left[ -\frac{7}{2};-\frac{1}{2} \right]\cup \left( 0;+\infty \right)\)
\( \displaystyle y<8\Rightarrow 4x+\frac{7}{x}<8\Rightarrow \frac{4{{x}^{2}}-8x+7}{x}<0\)
\( \displaystyle 4{{x}^{2}}-8x+7>0\) при всех \( \displaystyle x\), так как \( \displaystyle D=64-4\cdot 4\cdot 7=-48<0.\)
Значит, неравенство равносильно следующему: \( \displaystyle \frac{1}{x}<0\Rightarrow x<0\).
\( \displaystyle y\ge -16\Rightarrow 4x+\frac{7}{x}\ge 9\Rightarrow \frac{4{{x}^{2}}-9x+7}{x}\ge 0\).
\( \displaystyle 4{{x}^{2}}-9x+7>0\) при всех \( \displaystyle x\), так как \( \displaystyle D=81-4\cdot 4\cdot 7=-31<0.\)
Значит, неравенство равносильно следующему: \( \displaystyle \frac{1}{x}\ge 0\Rightarrow x>0\)
\( \displaystyle y<10\Rightarrow 4x+\frac{7}{x}<10\Rightarrow \frac{4{{x}^{2}}-10x+7}{x}<0\)
\( \displaystyle 4{{x}^{2}}-10x+7>0\) при всех \( \displaystyle x\), так как \( \displaystyle D=100-4\cdot 4\cdot 7=-12<0\).
Значит, неравенство равносильно следующему: \( \displaystyle \frac{1}{x}<0\Rightarrow x<0\).
Итак, неравенство оказывается равносильно совокупности:
\( \displaystyle \left[ \begin{array}{l}\left\{ \begin{array}{l}y\ge -16;\\y<8;\end{array} \right.\\\left\{ \begin{array}{l}y\ge 9;\\y<10;\end{array} \right.\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x\in \left[ -\frac{7}{2};-\frac{1}{2} \right]\cup \left( 0;+\infty \right)\\x<0\end{array} \right.\\\left\{ \begin{array}{l}x>0\\x<0\end{array} \right.\end{array} \right.\Rightarrow x\in \left[ -\frac{7}{2};-\frac{1}{2} \right].\)
Ответ: \( \displaystyle \left[ -\frac{7}{2};-\frac{1}{2} \right]\).
Замена переменных – один из важнейших методов решения уравнений и неравенств.
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



огромное спасибо за ваши разработки задач. очень интересно.
Пожалуйста! Рады, что понравилось!
Огромное Спасибо и море уважения — Ваша работа — это что-то потрясающее!
Нигде не видел такой тщательной проработки материала и такой удачной, продуманной подачи его.
С огромным уважением Александр Сорокин, Севастополь.
Спасибо, большое, Александр, за такой отзыв!