Рациональные уравнения
Рациональные уравнения – это уравнения, в которых и левая, и правая части – рациональные выражения.
Ну… Это было сухое математическое определение, и слово-то какое: «рациональные». А по сути, рациональные выражения – это просто целые и дробные выражения без знака корня.
Что же получается?
А получается, что под пугающим «рациональным уравнением» скрывается всего лишь уравнение, в котором могут присутствовать сложение, вычитание, умножение, деление и возведение в степень с целым показателем, но НЕ корень из переменной.
Давай подробнее…
Рациональные уравнения — коротко о главном
Определение рационального уравнения:
Рациональное уравнение – это равенство двух рациональных (без знака корня) выражений.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
Алгоритм решения рациональных уравнений:
- Понять, точно ли это рациональное уравнение (убедись, что в нем нет корней);
- Определить ОДЗ;
- Найти общий знаменатель дробей и умножить на него обе части уравнения;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль знаменатель дробей.
Система для решения дробно рациональных уравнений:
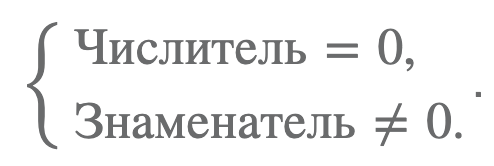
Что такое рациональные уравнения?
Давай научимся отличать рациональные уравнения от иррациональных! Зачем? Рациональные уравнения решать проще.
А зачем работать больше, если можно работать меньше?
- \( \displaystyle 3\cdot (x+1)=x\) как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное;
- \( \displaystyle 3\cdot (x+1)=\sqrt{x}\) – вот тебе и корень из переменной, значит уравнение НЕ рациональное (иррациональное);
- \( \displaystyle 3\cdot (x+1)=\frac{1}{x}\) а это – рациональное;
- \( \displaystyle 3\cdot (x+1)={{x}^{2}}\) тут вот степень, но она с целым показателем степени (\( \displaystyle 2\)– целое число) – значит это тоже рациональное уравнение;
- \( \displaystyle 3\cdot (x+1)={{x}^{-1}}\) даже уравнение с отрицательным показателем степени тоже является рациональным, ведь по сути \( \displaystyle {{x}^{-1}}\), это \( \displaystyle \frac{1}{x}\);
- \( \displaystyle 3\cdot (x+1)={{x}^{0}}\) – тоже рациональное, т.к. \( \displaystyle {{x}^{0}}=1\);
- \( \displaystyle 3\cdot (x+1)={{x}^{\frac{1}{2}}}\) – а с ним поосторожнее, степень-то дробная, а по свойству корней \( \displaystyle {{x}^{\frac{1}{2}}}=\sqrt{x}\), как ты помнишь, корня в рациональных уравнениях не бывает.
Надеюсь, теперь ты сможешь различать, к какому виду относится уравнение. (И не поедешь из Москвы в Петербург через Магадан, решая рациональные уравнения как нерациональные).
Целые рациональные уравнения
Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.
Если в дроби нет деления на переменную (то есть на \( \displaystyle x\), \( \displaystyle y\) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:
\( \displaystyle \begin{array}{l}\frac{2x}{3}=13-\frac{3x}{2};\\4(2y-3)=y-9.\end{array}\)
Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.
Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:
\( \displaystyle \frac{2x}{3}+\frac{3x}{2}=13\);
Какой наименьший общий знаменатель будет?
Правильно \( \displaystyle 6\)!
Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на \( \displaystyle 2\), а второго на \( \displaystyle 3\), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.
А \( \displaystyle 13\) не трогаем, оно нам не мешает, имеем:
\( \displaystyle \frac{4x}{6}+\frac{9x}{6}=13\)
\( \displaystyle \frac{13x}{6}=13\),
А теперь делим обе части на \( \displaystyle 13\):
\( \displaystyle \begin{array}{l}\frac{x}{6}=1\\x=6\end{array}\)
Тут все просто?
Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, \( \displaystyle 6\), так \( \displaystyle 6\), ну можно для верности подставить этот ответ в исходное уравнение, получим \( \displaystyle 0=0\), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).
Дробно-рациональные уравнения
А вот еще одно уравнение \( \displaystyle \frac{5}{x+1}+\frac{4{x}-6}{(x+1)\cdot (x+3)}=3\).
Это уравнение целое? НЕТ!!! Тут есть деление на переменную \( \displaystyle x\), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет \( \displaystyle (x+1)\cdot (x+3)\).
Важный момент!
В предыдущем примере, где было целое уравнение мы не стали свободный член \( \displaystyle 13\) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель \( \displaystyle (x+1)\cdot (x+3)\).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
\( \displaystyle \frac{5(x+1)\cdot (x+3)}{x+1}+\frac{(4{x}-6)\cdot (x+1)\cdot (x+3)}{(x+1)\cdot (x+3)}=3\cdot (x+1)\cdot (x+3)\).
Что-то оно огромное получилось, надо все посокращать:
\( \displaystyle 5(x+3)+(4{x}-6)=3\cdot (x+1)\cdot (x+3)\).
Раскроем скобки и приведем подобные члены:
\( \displaystyle \begin{array}{l}9x+9=3{{x}^{2}}+12x+9\\3{{x}^{2}}+3x=0.\end{array}\)
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: \( \displaystyle 3x\cdot (x+1)=0\)
У этого уравнения два решения, его левая сторона принимает нулевое значение при \( \displaystyle x=0\) и \( \displaystyle x=-1\).
Вроде бы все, ну ладно давайте напоследок подставим корни \( \displaystyle x=0\) и \( \displaystyle x=-1\) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим \( \displaystyle 0\), получается \( \displaystyle 3=3\) –нет претензий?
С ним все нормально. А теперь \( \displaystyle -1\), и тут же видим в знаменателе первого члена \( \displaystyle -1+1\)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ — Области Допустимых Значений!
(если забыл что это, повтори тему «ОДЗ — область допустимых значений»!)
Всякий раз когда ты видишь уравнение, где есть переменные (\( \displaystyle x,y\) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.
Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: \( \displaystyle x+1\ne 0\) и \( \displaystyle x+3\ne 0\) \( \displaystyle \Rightarrow x\ne -1\) и \( \displaystyle x\ne -3\).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами \( \displaystyle x=0\) и \( \displaystyle x=-1\) мы смело исключаем \( \displaystyle x=-1\), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, \( \displaystyle x=0\).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Алгоритм решения рационального уравнения
- Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);
- Определить ОДЗ;
- Найти общий знаменатель дробей и умножить на него обе части уравнения;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль знаменатель дробей.
Усвоил, говоришь? А ты докажи! 🙂 Вот тебе примеры на закрепление. Попробуй решить сам, а потом сверься с ответом.
Три примера на закрепление
- \( \displaystyle \frac{x-1}{2}+\frac{2x}{3}=\frac{5x}{6};\)
- \( \displaystyle \frac{x-3}{x-5}+\frac{1}{x}=\frac{x+5}{x(x-5)};\)
- \( \displaystyle \frac{33+{{x}^{2}}}{9-{{x}^{2}}}+\frac{7+x}{x-3}=-2+\frac{4-x}{x+3}.\)
Справился? Давай проверим:
Рациональные выражения, уравнения и дробно-рациональные уравнения
Повторим еще раз то, что прошил в предыдущих разделах, больше используя язык математики.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной \( \displaystyle x\) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Ну а рациональное уравнение – это равенство двух рациональных выражений.
Дробно-рациональные уравнения – рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.
Например:
\( \displaystyle \frac{{{x}^{2}}-2{x}-3}{{x}-1}-\frac{x+1}{{x}-3}={{x}^{2}}-1\) (чаще всего мы встречаем именно дробно рациональные уравнения).
В общем случае при решении рациональных уравнений мы стремимся преобразовать его к виду: Произведение = «\( \displaystyle 0\)» или Дробь = «\( \displaystyle 0\)«, например:
\( \displaystyle \frac{\left( {x}-2 \right)\left( x+3 \right)\left( {{x}^{2}}+1 \right)}{x\cdot \left( {x}-3 \right)}=0\).
Тогда мы сможем сказать, что любой из множителей числителя может быть равен нулю, но знаменатель при этом нулю не равен.
Для этого нам нужно сначала всё перенести в левую часть уравнения (не забываем при этом поменять знаки между слагаемыми: «\( \displaystyle +\)» на «\( \displaystyle —\)» и наоборот).
Затем мы обычно приводим все к общему знаменателю, и пишем систему:
\( \displaystyle \left\{ \begin{array}{l}Числитель=0,\\Знаменатель\ne 0.\end{array} \right.\)Например:
\( \displaystyle \begin{array}{l}\frac{{x}-2}{{{x}^{2}}+2{x}-3}-\frac{x+1}{{{x}^{2}}+5x+6}=\frac{3}{x+3}\Leftrightarrow \\\Leftrightarrow \frac{{x}-2}{\left( {x}-1 \right)\left( x+3 \right)}-\frac{x+1}{\left( x+2 \right)\left( x+3 \right)}-\frac{3}{x+3}=0\Leftrightarrow \end{array}\) \( \displaystyle \Leftrightarrow \frac{{{x}^{2}}-4-\left( {{x}^{2}}-1 \right)-3\left( {{x}^{2}}+{x}-2 \right)}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}=0\Leftrightarrow \frac{-3{{x}^{2}}-3x+3}{\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)}=0\Leftrightarrow \) \( \displaystyle \Leftrightarrow \left\{ \begin{array}{l}{{x}^{2}}+{x}-1=0\\\left( {x}-1 \right)\left( x+2 \right)\left( x+3 \right)\ne 0\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x=\frac{-1+\sqrt{5}}{2}\\x=\frac{-1-\sqrt{5}}{2}\end{array} \right.\\x\ne 1\\x\ne -2\\x\ne -3\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}x=\frac{-1+\sqrt{5}}{2}\\x=\frac{-1-\sqrt{5}}{2}.\end{array} \right.\)Если знаменателя нет, или он является числом, – тем лучше, не придется решать неравенство.
Как бы то ни было, в ЕГЭ все рациональные выражения степени больше \( \displaystyle 2\) легко преобразуются в произведение более простых выражений при помощи либо перегруппировки, либо замены переменных (см. раздел «Разложение многочлена на множители»).
Преобразование рационального выражения в более простое
Перегруппировка и замена переменных
\( \displaystyle \left( {x}-1 \right)\left( {x}-7 \right)\left( {x}-4 \right)\left( x+2 \right)=40.\)
Перегруппируем: \( \displaystyle \left( {x}-1 \right)\left( {x}-4 \right)\cdot \left( {x}-7 \right)\left( x+2 \right)=40;\)
Раскроем скобки в каждой группе: \( \displaystyle \left( {{x}^{2}}-5{x}+4 \right)\left( {{x}^{2}}-5{x}-14 \right)=40;\)
Сделаем замену: \( \displaystyle t={{x}^{2}}-5x.\)
Тогда:
Таким образом, нам пришлось решить три квадратных уравнения вместо одного уравнения 4-й степени.
Примеры дробно-рациональных уравнений
Попробуй сначала решить их самостоятельно, а потом посмотри решения.
- \( \displaystyle \frac{2{x}-3}{3{x}-7}=1\);
- \( \displaystyle \frac{1}{{x}-3}=\frac{1}{{{x}^{2}}-5x+6}\);
- \( \displaystyle \frac{1}{x+\frac{1}{1+\frac{x+2}{{x}-2}}}=\frac{12}{12{x}-7}\).
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике (практика решения задач)
ЕГЭ 15 Рациональные и иррациональные уравнения и неравенства. Метод интервалов
В этом видео ты узнаешь (вспомнишь) метод интервалов, поймёшь как и почему он работает.
Вспомнишь, как решать не только рациональные уравнения, но и квадратные, рациональные неравенства, а также неравенства с модулем и иррациональные.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Я иранец, и я счастлив узнать больше о математике. Это было хорошо. Большое спасибо
Спасибо, большое Porya! Вы хорошо знаете русский, если умеете читать такие тексты. Очень приятно!
Некоторые комментарии прошлых лет к этой статье:
Юля
19 марта 2018
Очень информативно! Спасибо)
ответить
Карина
05 ноября 2018
спасибо большое всё понятно и ясно ) даже очень понравилось рассказала друзьям теперь всё знаем ещё раз спасибо . ))) хи