Математическая статистика — основы
Слово «статистика» происходит от латинского слова «status» (статус), что означает «состояние и положение дел/вещей».
Статистика занимается изучением количественной стороны массовых общественных явлений и процессов в числовой форме, выявляя особые закономерности.
На сегодняшний день статистика применяется практически во всех сферах общественной жизни, начиная от моды, кулинарии, садоводства и заканчивая астрономией, экономикой, медициной.
Перво-наперво, при знакомстве со статистикой необходимо изучить основные статистические характеристики, применяемые для анализа данных.
Ну вот, с этого и начнем!
Математическая статистика — коротко о главном
Определения математической статистики:
Статистическая выборка – выбранное из всего числа объектов конкретное число объектов для исследования.
Объем выборки – количество элементов \( {{x}_{1}},{{x}_{2}},\ …,\ {{x}_{n}}\), попавших в выборку.
Размах выборки – разность между максимальным и минимальным значениями элементов выборки.
Или, размах выборки \( ={{x}_{\max }}-{{x}_{\min }}\)
Среднее арифметическое ряда чисел – это частное от деления суммы этих чисел на их количество (объем выборки).
Среднее арифметическое ряда чисел \( \left( {{x}_{cp.}} \right)\) – это частное от деления суммы этих чисел \( \left( {{x}_{1}}+{{x}_{2}}+…+{{x}_{n}} \right)\) на их количество \( \left( n \right)\)
Или: \( {{x}_{cp.}}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+…+{{x}_{n}}}{n}\)
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Медиана упорядоченного ряда чисел с нечетным числом членов – число, которое окажется посередине.
Медиана упорядоченного ряда чисел с четным числом членов –среднее арифметическое двух чисел, записанных посередине.
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
или…
Частота – число повторений определенного значения параметра в выборке.
Относительная частота – это отношение частоты к общему числу данных в ряду.
Для наглядности удобно представлять данные в виде соответствующих диаграмм/графиков.
Статистические характеристики
К основным статистическим характеристикам выборки данных…
Какая еще такая «выборка»!?
Под словом «выборка» подразумевается просто данные, которые ты собираешься исследовать.
Дальше на примерах будет все понятно.
Так вот к основным статистическим характеристикам выборки данных относятся:
- объем выборки,
- размах выборки,
- среднее арифметическое,
- мода,
- медиана,
- частота,
- относительная частота.
Стоп-стоп-стоп! Сколько новых слов! Давай обо всем по порядку.
Объем и размах выборки
Выборка состоит из элементов \( {{x}_{1}},{{x}_{2}},\ …,\ {{x}_{n}}\), попавших в нее. Количество этих элементов \( \left( n \right)\) называется объемом выборки.
Например, в таблице ниже приведен рост игроков сборной по футболу:

Данная выборка представлена \( \displaystyle 11\) элементами \( \displaystyle \left( {{x}_{1}}=183;\ {{x}_{2}}=194;\ {{x}_{3}}=187;\ …;\ {{x}_{11}}=181 \right)\).
Таким образом, объем выборки \( \displaystyle \left( n \right)\) равен \( \displaystyle 11\).
Разность между максимальным и минимальным значениями элементов выборки называется размахом выборки.
Или, размах выборки \( ={{x}_{\max }}-{{x}_{\min }}\)
Размах представленной выборки составляет \( {{x}_{\max }}-{{x}_{\min }}=194-176=18\) см.
Среднее арифметическое выборки
Среднее арифметическое ряда чисел \( \left( {{x}_{cp.}} \right)\) – это частное от деления суммы этих чисел \( \left( {{x}_{1}}+{{x}_{2}}+…+{{x}_{n}} \right)\) на их количество \( \left( n \right)\).
Или, \( {{x}_{cp.}}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+…+{{x}_{n}}}{n}\).
Не очень понятно? Давай смотреть на наш пример.

Определите средний рост игроков.
Ну что, приступим? Мы уже разбирались, что \( \displaystyle {{x}_{1}}=183;\ {{x}_{2}}=194;\ {{x}_{3}}=187;\ …;\ {{x}_{11}}=181\); \( \displaystyle n=11\).
Можем сразу смело все подставлять в нашу формулу:
\( \displaystyle {{x}_{cp.}}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+…+{{x}_{n}}}{n}\)
\( \displaystyle {{x}_{cp.}}=\frac{183+194+187+181+176+190+189+184+178+179+181}{11}=183,8\)
Таким образом, средний рост игрока сборной составляет \( \displaystyle 183,8\) см.
Ну или вот такой пример:
Ученикам 9 класса на неделю было задано решить как можно больше примеров из задачника. Количество примеров, решенных учениками за неделю, приведены ниже:

Найдите среднее количество решенных задач.
Итак, в таблице нам представлены данные по \( \displaystyle 20\) ученикам. Таким образом, \( \displaystyle n=20\). \( \displaystyle {{x}_{1}}=88;\ {{x}_{2}}=90;\ {{x}_{3}}=51;\ …;\ {{x}_{20}}=47.\)
Ну что ж, найдем для начала сумму (общее количество) всех решенных задач двадцатью учениками:
\( \displaystyle \begin{array}{l}88+90+51+85+58+105+77+89+100+109+77+83+92+77+\\+44+81+50+77+80+47=1560\end{array}\)
Теперь можем смело приступать к расчету среднего арифметического решенных задач, зная, что \( \displaystyle {{x}_{1}}+{{x}_{2}}+…+{{x}_{n}}=1560\), а \( \displaystyle n=20\):
\( \displaystyle {{x}_{cp.}}=\frac{1560}{20}=78\).
Таким образом, в среднем ученики 9 класса решили по \( \displaystyle 78\) задач.
Еще один пример:
На рынке помидоры реализуются \( \displaystyle 7\) продавцами, причем цены за \( \displaystyle 1\) кг распределены следующим образом (в руб.): \( \displaystyle 60,\text{ }55,\text{ }54,\text{ }70,\text{ }65,\text{ }67,\text{ }63\).
Какова средняя цена килограмма помидоров на рынке?
Решение.
Итак, чему в данном примере равно \( \displaystyle n\)? Все верно: семь продавцов предлагают семь цен, значит, \( \displaystyle n=7\)! \( \displaystyle {{x}_{1}}=60;\ {{x}_{2}}=55;\ …;\ {{x}_{n}}=63\).
Ну вот, со всеми составляющими разобрались, теперь можем приступить к расчету средней цены:
\( \displaystyle {{x}_{cp.}}=\frac{{{x}_{1}}+{{x}_{2}}+…+{{x}_{n}}}{n}=\frac{60+55+54+70+65+67+63}{7}=\frac{434}{7}=62\) (рубля)
Ну что, разобрался?
Тогда посчитай самостоятельно среднее арифметическое в следующих выборках:
- \( \displaystyle 34;\ 46;\ 67;\ 37;\ 45;\text{ }60\)
- \( \displaystyle 5;\ 4;\ 7;\ 9;\ 10;\ 12;\ 17;\ 8\)
- \( \displaystyle 156;\ 180;\ 164;\ 172\)
Ответы: \( \displaystyle 48,17;\text{ }9;\ 168\).
Решил? Можем двигаться дальше.
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:

Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число \( \displaystyle 181\), так как два игрока имеют рост \( \displaystyle 181\) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?

Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:


Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков \( \displaystyle 11\), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас \( \displaystyle 11\), значит, по краям остается по пять чисел, а рост \( \displaystyle 183\) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
А теперь разберем пример с нашими отчаянными ребятами из 9 класса, которые решали примеры в течение недели:

Готов искать в этом ряду моду и медиану?
Для начала, упорядочим этот ряд чисел (расположим от самого маленького числа к самому большому). Получился вот такой вот ряд:

Теперь можно смело определить моду в данной выборке. Какое число встречается чаще других? Все верно, \( \displaystyle 77\)!
Таким образом, мода в данной выборке равна \( \displaystyle 77\).
Моду нашли, теперь можем приступать к нахождению медианы. Но прежде, ответь мне: каков объем рассматриваемой выборки? Посчитал? Все верно, объем выборки равен \( \displaystyle 20\).
А \( \displaystyle 20\) – это четное число. Таким образом, применяем определение медианы для ряда чисел с четным количеством элементов.
То есть нам надо в нашем упорядоченном ряду найти среднее арифметическое двух чисел, записанных посередине. Какие два числа располагаются посередине?
Все верно, \( \displaystyle 80\) и \( \displaystyle 81\)!

Таким образом, медианой этого ряда будет среднее арифметическое чисел \( \displaystyle 80\) и \( \displaystyle 81\):
\( \frac{80+81}{2}=\frac{161}{2}=80,5\)\( 80,5\)— медиана рассматриваемой выборки.
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:

Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост \( 176\)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом \( 176\) в нашей выборке равна \( 1\).
Сколько игроков имеет рост \( 178\)? Да, опять же один игрок. Частота встречи игрока с ростом \( 178\) в нашей выборке равна \( 1\).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:

Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: \( 1+1+1+2+1+1+1+1+1+1=11\)
Перейдем к следующей характеристике – относительная частота.
| Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах. |
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем \( \left( n=11 \right)\) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:

А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
Графическое изображение данных
Очень часто для наглядности данные представляются в виде диаграмм/графиков. Остановимся на рассмотрении основных из них:
- столбчатая диаграмма,
- круговая диаграмма,
- гистограмма,
- полигон.
Столбчатая диаграмма
Столбчатые диаграммы используют тогда, когда хотят продемонстрировать динамику изменения данных во времени или распределения данных, полученных в результате статистического исследования.
Например, у нас есть вот такие данные об оценках написанной контрольной работы в одном классе:

Количество получивших такую оценку – это у нас и есть частота. Зная это, мы можем составить вот такую вот табличку:
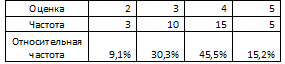
Теперь мы можем построить наглядные столбчатые графики на основе такого показателя как частота (на горизонтальной оси отражены оценки \( \displaystyle \left( 2,3,4,5 \right)\) на вертикальной оси откладываем количество учеников, получивших соответствующие оценки):
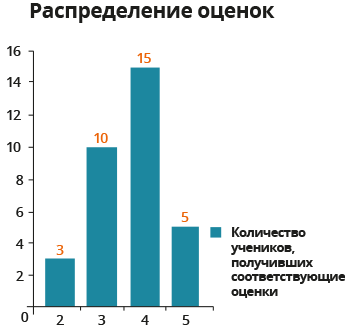
Или же можем построить соответствующий столбчатый график на основе относительной частоты:
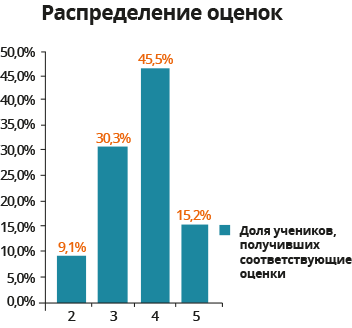
Рассмотрим пример по типу задания из ЕГЭ.
Пример.
На диаграмме показано распределение добычи нефти в \( \displaystyle 7\) странах мира (в тоннах) за 2011 год.
Среди стран первое место по добыче нефти занимала Саудовская Аравия, седьмое место – Объединенные Арабские Эмираты. Какое место занимали США?
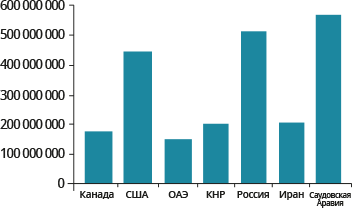
Ответ: третье.
Круговая диаграмма
Для наглядного изображения соотношения между частями исследуемой выборки удобно использовать круговые диаграммы.
По нашей табличке с относительными частотами распределения оценок в классе мы можем построить круговую диаграмму, разбив круг на секторы, пропорциональные относительным частотам.
Вот так:
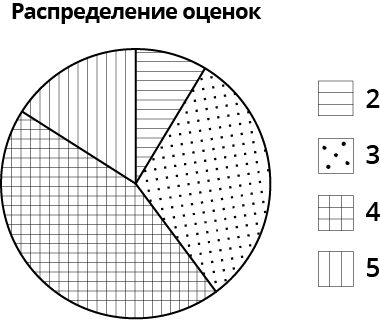
Круговая диаграмма сохраняет свою наглядность и выразительность только при небольшом числе частей совокупности. В нашем случае, таких частей четыре (в соответствии с возможными оценками \( \displaystyle 2,3,4,5\)), поэтому применение такого типа диаграммы достаточно эффективно.
Рассмотрим пример по типу задания 18 из ГИА.
Пример.
На диаграмме показано распределение расходов семьи во время отдыха на море. Определите, на что семья потратила больше всего?
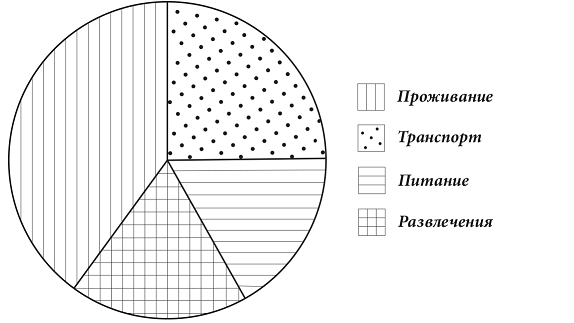
Ответ: проживание.
Полигон
Динамику изменения статистических данных во времени часто изображают с помощью полигона.
Для построения полигона отмечают в координатной плоскости точки, абсциссами которых служат моменты времени, а ординатами – соответствующие им статистические данные.
Соединив последовательно эти точки отрезками, получают ломанную, которую называют полигоном.
Вот, к примеру, нам даны среднемесячные температуры воздуха в Москве.

Сделаем приведенные данные более наглядными – построим полигон.
На горизонтальной оси отражены месяцы, на вертикальной – температура. Строим соответствующие точки и соединяем их.
Вот, что получилось:
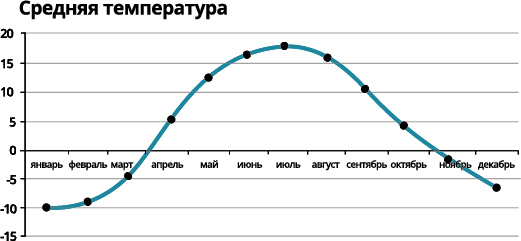
Согласись, сразу стало наглядней!
Полигон, используют также для наглядного изображения распределения данных, полученных в результате статистического исследования.
Вот построенный полигон на основе нашего примера с распределением оценок:

Рассмотрим типовое задание из ЕГЭ.
Пример.
На рисунке жирными точками показана цена алюминия на момент закрытия биржевых торгов во все рабочие дни с \( \displaystyle 7\) по \( \displaystyle 20\) августа \( \displaystyle 2014\) года.
По горизонтали указываются числа месяца, по вертикали — цена тонны алюминия в долларах США. Для наглядности жирные точки на рисунке соединены линией.
Определите по рисунку, какого числа цена алюминия на момент закрытия торгов была наименьшей за данный период.
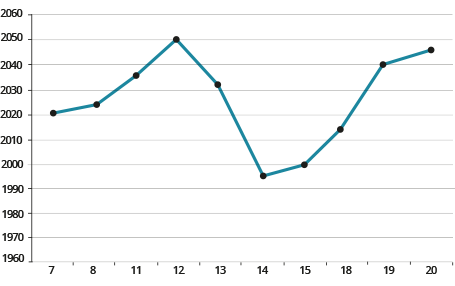
Ответ: \( \displaystyle 14\).
Гистограмма
Интервальные ряды данных изображают с помощью гистограммы.
Гистограмма представляет собой ступенчатую фигуру, составленную из сомкнутых прямоугольников. Основание каждого прямоугольника равно длине интервала, а высота – частоте или относительной частоте.
Таким образом, в гистограмме, в отличие от обычной столбчатой диаграммы, основания прямоугольника выбираются не произвольно, а строго определены длиной интервала.
Вот, к примеру, у нас есть следующие данные о росте игроков, вызванных в сборную:
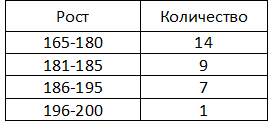
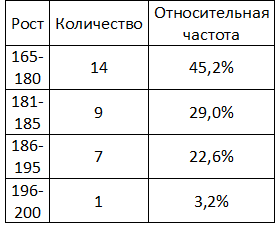
Итак, нам дана частота (количество игроков с соответствующим ростом). Мы можем дополнить табличку, рассчитав относительную частоту:
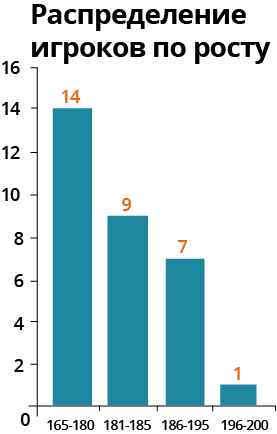
Ну вот, теперь можем строить гистограммы. Сначала построим на основании частоты.
Вот, что получилось:
А теперь на основании данных об относительной частоте:
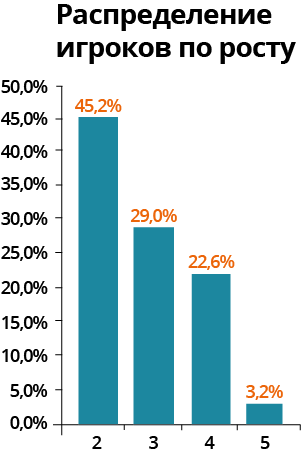
Пример.
На выставку по инновационным технологиям приехали представители \( \displaystyle 50\) компаний. На диаграмме показано распределение этих компаний по количеству персонала.
По горизонтали представлено количество сотрудников в компании, по вертикали — количество компаний, имеющих данное число сотрудников.
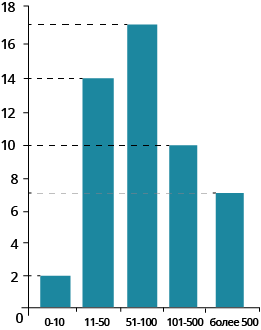
Какой процент составляют компании с общим числом сотрудников больше \( \displaystyle 50\) человек?
Ответ: \( \displaystyle 68\%\).
Бонус: Вебинары с нашего курса по подготовке к ЕГЭ
Этот вебинар по родственной математической статистике теме — теории вероятности.
А вот наша статья о теории вероятности.
ЕГЭ №4 Теория вероятности
Что вы узнаете на этом уроке?
20% урока — теория.
- Мы разберём, что такое вероятность;
- Узнаем, что можно называть случайным событием;
- Рассмотрим, на какие типы можно разделить события:
- Что такое совместные и несовместные события;
- Что такое зависимые и независимые события;
- Выучим формулы, которые нужно применять для разных типов событий.
80% урока — решение задач
- Мы решим 54 задачи на первом уроке и ещё 22 (посложнее) на втором;
- Отработаем все 6 типов задач, которые могут встретиться в ЕГЭ:
Подготовка к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org
А теперь твоя очередь!
Сейчас мы хотим услышать тебя. Напиши комментарий ниже и расскажи нам, помогла ли тебе эта статья? Какой момент показался самым сложным? Разобрался ли ты в нем?
А еще мы ответим на любые твои вопросы.
Очень важно уметь решать задачи на статистику. И сегодня ты не просто разобрал «еще один тип задач на экзамене», но и получил очень полезный навык.
Слышал когда-нибудь про data science? Если нет, поищи информацию в интернете. Удивлю ли я тебя, сказав, что ты уже научился делать очень многое, что относится к этой науке? Ведь ее основа – статистический анализ.
Удачи!



Неплохо бы посмотреть или почитать про распределение пуассонов
Да, пуассоны, к сожалению (или к счастью), в школьную программу не входят)
Но могу посоветовать почитать вот здесь: http://mathprofi.ru/raspredelenie_i_formula_puassona.html
спасибо огоромное)
И вам спасибо, Максон. Удача!