Линейные неравенства
Раз уж ты читаешь эту тему, то ты наверняка уже знаком с темой «Линейные уравнения».
Если нет, то лучше скорей отправляйся исправлять это недоразумение.
Без усвоенной этой темы спокойное плавание в линейных неравенствах не гарантировано.
А если тебе все с ними понятно, вперед, покорять неравенства.
Линейные неравенства — коротко о главном
Линейными неравенствами называются неравенства вида:
\( \displaystyle ax+b<0\)где \( \displaystyle a\) и \( \displaystyle b\) – любые числа, причем \( \displaystyle a\ne 0\); \( \displaystyle x\) — неизвестная переменная.
Правила преобразования неравенств:
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак \( \displaystyle >\) на знак \( \displaystyle <\), и наоборот; знак \( \displaystyle \ge \)на знак \( \displaystyle \le \), и наоборот).
Что такое линейное неравенство
Неформальное объяснение
Если ты ознакомился с линейными уравнениями, то уже знаком с Васей, который раздавал яблоки своим друзьям.
Так вот, предположим, что у Васи больше, чем \( \displaystyle 12\) яблок. Все свои яблоки он хочет раздать поровну троим друзьям. По сколько яблок получит каждый друг?
Если обозначить через \( \displaystyle x\) количество яблок, которое достанется каждому из трех друзей, то получим следующее линейное неравенство:
\( \displaystyle 3x>12\)
Дальше мы делим обе части составленного неравенства на \( \displaystyle 3\) и получаем:
\( \displaystyle x>\frac{12}{3}\)
\( \displaystyle x>4\)
Таким образом, каждый друг щедрого Васи получит больше, чем \( \displaystyle 4\) яблока.
Ну вот и справились с неравенством! Сейчас я введу формализованное определение линейного неравенства и будем разбираться с ним дальше.
Определение линейного неравенства:
Линейные неравенства — это неравенства вида:
\( \displaystyle ax+b>0\)
\( \displaystyle ax+b\ge 0\)
\( \displaystyle ax+b\le 0\)
где \( \displaystyle a\) и \( \displaystyle b\) – любые числа, причем \( \displaystyle a\ne 0\); \( \displaystyle x\) — неизвестная переменная.
Например:
\( \displaystyle 5x>16\)
\( \displaystyle \frac{4}{7}x+7<0\)
\( \displaystyle \frac{2}{3}x\ +8\ge 0\)
\( \displaystyle 4x\le -\frac{15}{19}\)
Все приведенные выше неравенства являются линейными.
Во всех них «сидит» очень важная особенность: в таких неравенствах нет иксов в квадрате, в кубе и т.д., кроме того в этих неравенствах нет деления на икс и икс не находится под знаком корня.
Чтобы лучше распознавать линейные неравенства, настоятельно рекомендую тебе еще раз заглянуть в раздел «Скрытые» линейные уравнения или…» темы «Линейные уравнения».
Линейные неравенства обладают не меньшим талантом «скрываться».
Чтобы не попасть впросак и с легкостью преобразовывать любые неравенства, надо знать и успешно применять 3 очень важных правила. Эти знания здорово упростят тебе жизнь на пути решения неравенств.
3 правила преобразования неравенств
Два неравенства равносильны, если они имеют одинаковые решения.
Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
Для упрощения процесса нахождения всех корней неравенства проводятся равносильные преобразования, то есть проводится замена данного неравенства более простым, при этом не должны потеряться никакие решения и не должно возникнуть никаких посторонних корней.
В общем, это все пока только слова. Давай разбираться прямо на правилах.
Правило №1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные).
Например,
\( \displaystyle 3{x}-4>7\text{ }\Rightarrow 3x>7+4\Rightarrow 3x>11\)
Таким образом, можно с уверенностью сказать, что \( \displaystyle 3{x}-4>7\) равносильно \( \displaystyle 3x>11\).
Или вот такой пример:
\( \displaystyle 12+4x\le 7-3x\)
В теме «Линейные уравнения» говорилось, что для удобства принято переносить слагаемые с переменной в левую часть, а остальные в правую – так и поступим:
\( \displaystyle 12+4x\le 7-3x\)
\( \displaystyle 12+4x\le 7-3x\)
\( \displaystyle 4x+3x\le 7-12\)
\( \displaystyle 7x\le -5\)
Здесь все должно быть понятно, перейдем к следующему правилу.
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Вернемся к нашим двум предыдущим примерам.
В первом примере мы остановились на \( \displaystyle 3x>11\). Применим правило 2, разделив обе части неравенства на положительное число \( \displaystyle 3\):
\( \displaystyle 3x>11\)
\( \displaystyle x>\frac{11}{3}\)
\( \displaystyle x>3\frac{2}{3}\)
Заметил, знак неравенства как был «больше», так и сохранился? Все это потому, что мы делили на положительное число.
Давай закрепим на втором примере, где мы остановились на \( \displaystyle 7x\le -5\). Разделим обе части неравенства на \( \displaystyle 7\):
\( \displaystyle 7x\le -5\)
\( \displaystyle x\le -\frac{5}{7}\)
Делили на положительное число \( \displaystyle 7\), поэтому знак неравенства сохранился.
Почему так акцентируется внимание на том, что знак неравенства \( \displaystyle \left( \le \right)\) сохраняется?
А вот потому, что в отличие от преобразований линейных уравнений, преобразования линейных неравенств имеют свою особенность, можно даже сказать «подводный камень». Что это за «камень» должно прояснить правило 3.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный
Иными словами, знак \( \displaystyle >\) на знак \( \displaystyle <\), и наоборот; знак \( \displaystyle \ge \) на знак \( \displaystyle \le \), и наоборот).
Заметил важное отличие от правила 2? Все верно:
- При умножении/делении на положительное число знак неравенства сохраняется
- При умножении/делении на отрицательное число знак неравенства меняется на противоположный
Например:
Делим на отрицательное число \( -4\), тогда знак неравенства меняется на противоположный:
\( \displaystyle -4x<3\)
\( \displaystyle x>-\frac{3}{4}\)
Заметил, знак \( \displaystyle <\) (меньше) заменили на знак \( \displaystyle >\) (больше)?
Или вот такой пример:
\( \displaystyle -7x\ge -8\)
Делим обе части на отрицательное число \( \displaystyle -7\), меняя при этом знак неравенства на противоположный:
\( \displaystyle -7x\ge -8\)
\( \displaystyle x\le \frac{8}{7}\)
Усвоил? Тогда давай закреплять на примерах.
Пять примеров для самостоятельной работы
Не пугайся, что примеры, на первый взгляд, сложней, чем мы с тобой разбирали. Мы ведь знаем все необходимые правила преобразования линейных неравенств, а значит, не пропадем.
Ну что, приступим? Как-никак, это не Эверест покорять.
1. \( \displaystyle 5\left( 14{x}-2 \right)+\frac{1}{4}\left( 12-4x \right)\ge 3\)
Раскроем для начала скобки и приведем подобные слагаемые:
\( \displaystyle 5\left( 14{x}-2 \right)+\frac{1}{4}\left( 12-4x \right)\ge 3\)
\( \displaystyle 5\cdot 14{x}-5\cdot 2+\frac{1}{4}\cdot 12-\frac{1}{4}\cdot 4x\ge 3\)
\( \displaystyle 70{x}-10+3-x\ge 3\)
\( \displaystyle 69{x}-7\ge 3\)
А теперь можем применять наши правила преобразования линейных неравенств:
2. \( \displaystyle 7\left( 3{x}-1 \right)+\frac{1}{3}\left( 6{x}-12 \right)\le 3\)
Все, как в первом примере: раскрываем скобки, приводим подобные слагаемые, осуществляем необходимые преобразования:
\( \displaystyle 7\left( 3{x}-1 \right)+\frac{1}{3}\left( 6{x}-12 \right)\le 3\)
\( \displaystyle 21{x}-7+2{x}-4\le 3\)
\( \displaystyle 23{x}-11\le 3\)
\( \displaystyle 23x\le 3+11\)
\( \displaystyle 23x\le 14\)
\( \displaystyle x\le \frac{14}{23}\)
Неравенство у нас нестрогое, поэтому число \( \displaystyle \frac{14}{23}\) включается в наш промежуток:
3. \( \displaystyle {{\left( x+2 \right)}^{2}}+{{\left( {x}-4 \right)}^{2}}\ge 2{{x}^{2}}\)
Думаешь это не линейное неравенство? А что мы говорили в теме Линейные уравнений об их «скрытности»?
Поспешных выводов делать не стоит, давай лучше проведем все возможные преобразования и убедимся, что это линейное неравенство, либо докажем обратное.
\( \displaystyle {{\left( x+2 \right)}^{2}}+{{\left( {x}-4 \right)}^{2}}\ge 2{{x}^{2}}\)
\( \displaystyle \left( {{x}^{2}}+4x+4 \right)+\left( {{x}^{2}}-8x+16 \right)\ge 2{{x}^{2}}\)
\( \displaystyle {{x}^{2}}+4x+4+{{x}^{2}}-8x+16\ge 2{{x}^{2}}\)
\( \displaystyle 2{{x}^{2}}-4x+20\ge 2{{x}^{2}}\)
\( \displaystyle 2{{x}^{2}}-2{{x}^{2}}-4x\ge -20\)
\( \displaystyle -4x\ge -20\)
Сейчас будем делить обе части неравенства на отрицательное число \( \displaystyle -4\). Что же тогда произойдет со знаком неравенства?
4. \( \displaystyle {{\left( {x}-6 \right)}^{2}}-{{\left( 5-x \right)}^{2}}<3\)
Проводим соответствующие преобразования:
\( \displaystyle {{\left( {x}-6 \right)}^{2}}-{{\left( 5-x \right)}^{2}}<3\)
\( \displaystyle \left( {{x}^{2}}-12x+36 \right)-\left( 25-10x+{{x}^{2}} \right)<3\)
\( \displaystyle {{x}^{2}}-12x+36-25+10{x}-{{x}^{2}}<3\)
\( \displaystyle -2x+11<3\)
\( \displaystyle -2x<3-11\)
\( \displaystyle -2x<-8\)
Делим обе части на отрицательное число \( \displaystyle \left( -2 \right)\), не забывая поменять знак неравенства на противоположный:
5. \( \displaystyle 4\left( 2-3x \right)>7-5x\)
Этот пример проще, поэтому сразу запишу ход решения без комментариев:
\( \displaystyle 4\left( 2-3x \right)>7-5x\) \( \displaystyle 8-12x>7-5x\) \( \displaystyle -12x+5x>7-8\) \( \displaystyle -7x>-1\) \( \displaystyle x<\frac{1}{7}\)Ответ: \( \displaystyle x\in \left( -\infty ;\frac{1}{7} \right)\)
Линейные неравенства с двумя переменными
В теме «Линейные уравнения» достаточно подробно разобрано понятие линейного уравнения с двумя переменными. Линейное неравенство представляет собой практически то же самое, только знак равенства меняется на знак неравенства \( \left( >,<,\ge ,\le \right)\).
Линейные неравенства с двумя переменными имеют вид:
\( ax+by+c>0\)
\( ax+by+c<0\)
\( ax+by+c\ge 0\)
\( ax+by+c\le 0\),
где \( a\), \( b\) и \( c\) – любые числа, \( a\ne 0\).
А вся разница с линейным неравенством с одной переменной только в том, что в неравенство добавляется еще одна переменная \( \left( y \right)\).
Решением неравенства с двумя переменными называется множество пар чисел \( \left( x;y \right)\), которые удовлетворяют этому неравенству (т.е. при подстановке этих точек неравенство верно).
Для решения линейных неравенств с двумя переменными, используется графический способ.
Графический способ решения линейных неравенств
Давай разберем вот такой пример:
\( 5x+4y>0\)Решение:
Как уже упоминалось, решается такое неравенство графически.
Построим график уравнения \( 5x+4y=0\). Как ты уже должен был знать из темы «Линейные уравнения», графиком будет прямая.
\( 5x+4y=0\) \( y=\frac{-5}{4}x\)Строим график по двум точкам, через которые проходит прямая, к примеру, \( B\left( 0;0 \right)\) и \( C\left( 4;-5 \right)\). Вот, что у меня получилось:
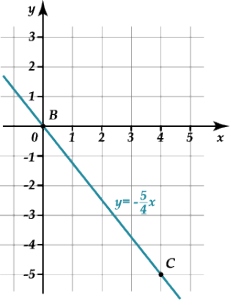
Так как неравенство в этом примере у нас строгое, то координаты точек самого графика прямой не будут являться решением исходного неравенства. Поэтому обозначим линию пунктиром на графике:
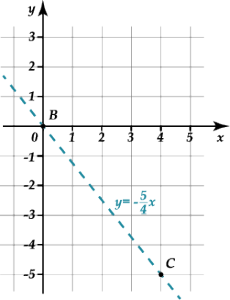
Как можно заметить, прямая разбила плоскость на две полуплоскости. Все точки одной из полуплоскостей будут являться решением исходного неравенства.
Так как в исходном неравенстве у нас стоит знак \( >\), то мы должны выбрать те точки, которые лежат выше графика прямой. Изобразим все решения неравенства на графике:
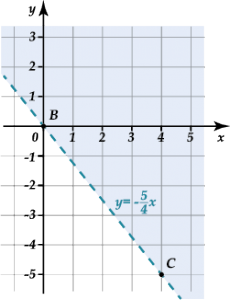
Все решения «затушеваны» голубым цветом. Вот и все, неравенство с двумя переменными решено. Это значит, что координаты \( x\) и \( y\) любой точки из закрашенной области – решения неравенства.
Бонус: вебинар из нашего курса подготовки к ЕГЭ по математике
Этот вебинар — на повторение линейных уравнений.
Линейные уравнения – основа всей алгебры. Научитесь решать линейные уравнения, и вам будет намного проще осваивать всё остальное (в том числе и линейные неравенства).
На вебинаре вы решите 65 (!) линейных уравнений, набьете руку, чтобы уж никогда не испытывать проблем с ними.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Тамара
21 октября 2017
Спасибо. всё чётко и ясно