Линейные уравнения
Линейные уравнения – основа всей алгебры.
Научись решать линейные уравнения, и тебе будет намного проще осваивать всю остальную алгебру!
Для этого нужно прочитать эту статью и посмотреть вебинар на линейные уравнения.
Посмотри также вебинары на решение других типов уравнений (в разделе «Бонусы»)
Поехали!
Линейные уравнения — коротко о главном
Линейное уравнение
Это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна \( \displaystyle 1\).
Линейное уравнение с одной переменной имеет вид:
\( \displaystyle ax+b=0\), где \( \displaystyle a\) и \( \displaystyle b\) – любые числа \( \displaystyle a\ne 0\);
Линейное уравнение с двумя переменными имеет вид:
\( \displaystyle ax+by+c=0\), где \( \displaystyle a\), \( \displaystyle b\) и \( \displaystyle c\)– любые числа \( \displaystyle a\ne 0\).
Тождественные преобразования
Не всегда сразу можно определить, является ли уравнение линейным или нет. Иногда, чтобы понять это, необходимо произвести тождественные преобразования:
- перенести влево/вправо подобные члены, не забыв изменить знак;
- умножить/разделить обе части уравнения на одного и тоже число.
Линейное уравнение — подробно
Все мы с детства знаем такую задачу: «У Васи есть \( \displaystyle 12\) яблок. Мальчик решил поделиться яблоками с \( \displaystyle 3\) друзьями. Сколько яблок досталось каждому другу?»
Каждый из нас, не задумываясь, ответит: «Каждому другу досталось по \( \displaystyle 4\) яблока».
Однако, отвечая на такой простой вопрос ты в голове решаешь линейное уравнение!
Смотри:
\( \displaystyle 3\cdot x=12\) или в устной форме – трем друзьям дали по \( \displaystyle x\) яблок из расчета, что всего в наличии у Васи \( \displaystyle 12\) яблок.
Соответственно, дальше ты находишь \( \displaystyle x\) путем деления произведения на известный тебе множитель:
\( \displaystyle x=\frac{12}{3}=4\)
И вот ты уже решил линейное уравнение…
Теперь дадим этому термину математическое определение.
Линейное уравнение – это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна \( \displaystyle 1\).
Оно выглядит следующим образом:
\( \displaystyle ax+b=0\), где \( \displaystyle a\) и \( \displaystyle b\) – любые числа и
\( \displaystyle a\ne 0\).
Для нашего случая с Васей и яблоками мы запишем:
\( \displaystyle 3\cdot {x}-12=0\) – «если Вася раздаст всем троим друзьям одинаковое количество яблок, у него яблок не останется»
Иными словами, линейное уравнение – это такое уравнение, у которого нет иксов в квадрате, в кубе и т.д., здесь есть дроби, но и нет иксов в знаменателях, т.е. нет деления на икс.
«Скрытые» линейные уравнения, или важность тождественных преобразований
Предыдущее определение выглядит все просто, да?
Однако надо быть внимательным, потому что линейными уравнениями называются не только уравнения вида \( \displaystyle ax+b=0\), но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду.
Например:
\( \displaystyle {{\left( {x}-6 \right)}^{2}}+{{\left( x+3 \right)}^{2}}=2{{x}^{2}}\)
Мы видим, что справа стоит \( \displaystyle {{x}^{2}}\), что, по идее, уже говорит о том, что уравнение не линейное.
Мало того, если мы раскроем скобки, то получим еще два слагаемых, в которых будет \( \displaystyle {{x}^{2}}\), но не надо торопиться с выводами!
Прежде, чем судить, является ли уравнение линейным, необходимо произвести все преобразования и таким образом, упростить исходный пример. При этом преобразования могут изменять внешний вид, но никак не саму суть уравнения.
Иными словами, данные преобразования должны быть тождественными или равносильными.
Таких преобразований всего два, но они играют очень, очень важную роль при решении задач. Рассмотрим оба преобразования на конкретных примерах.
Тождественные преобразования
Перенос влево-вправо
\( \displaystyle 15-2x=10+x\)
Еще в начальной школе нам говорили: «с иксами – влево, без иксов – вправо». Какое выражение с иксом стоит слеава? Правильно, \( \displaystyle -2x\), а не как не \( \displaystyle 2x\).
И это важно, так как при неправильном понимании этого, казалось бы простого вопроса, выходит неверный ответ. А какое выражение с иксом стоит справа? Правильно, \( \displaystyle +x\).
Теперь, когда мы с этим разобрались, переносим все слагаемые с неизвестными в левую сторону, а все, что известно – в правую, помня, что если перед числом нет никакого знака, например, \( \displaystyle 15\), то значит число положительно, то есть перед ним стоит знак «\( \displaystyle +\)».
ВАЖНО: при переносе через знак равенства, знаки при слагаемых меняются на противоположные.
Перенёс? Что у тебя получилось?
\( \displaystyle -2{x}-x=10-15\)
Все, что осталось сделать – привести подобные слагаемые. Приводим:
\( \displaystyle \begin{array}{l}-3x=-5\\x=\frac{5}{3}=1\frac{2}{3}\end{array}\)
Итак, первое тождественное преобразование мы успешно разобрали, хотя уверена, что ты и без меня его знал и активно использовал. Главное – не забывай про знаки при числах и меняй их на противоположные при переносе через знак равенства!
Умножение — деление
Начнем сразу же с примера
\( \displaystyle 4x=16\)
Смотрим и соображаем: что нам не нравится в этом примере? Неизвестное все в одной части, известные – в другой, но что-то нам мешает… И это что-то – четверка, так как если бы ее не было, все было бы идеально – икс равен числу – именно так, как нам и нужно!
Как можно от неё избавиться? Перенести вправо мы не можем, так как тогда нам нужно переносить весь множитель (мы же не можем ее взять и оторвать от \( \displaystyle x\)), а переносить весь множитель тоже не имеет смысла…
Пришло время вспомнить про деление, в связи с чем разделим все как раз на \( \displaystyle 4\)! Все – это означает и левую, и правую часть. Так и только так! Что у нас получается?
\( \displaystyle x=4\)
Вот и ответ.
Посмотрим теперь другой пример:
\( \displaystyle \frac{1}{2}x=3\)
Догадываешься, что нужно сделать в этом случае? Правильно, умножить левую и правую части на \( \displaystyle 2\)! Какой ты получил ответ? Правильно. \( \displaystyle 6\).
ВАЖНО: при делении, либо умножении на какое-либо число, действие совершается как в левой, так и в правой части уравнения
Наверняка все про тождественные преобразования ты и так уже знал. Считай, что мы просто освежили эти знания в твоей памяти и настало время для нечто большего…
Например, для решения нашего большого примера:
\( \displaystyle {{\left( {x}-6 \right)}^{2}}+{{\left( x+3 \right)}^{2}}=2{{x}^{2}}\)
Как мы уже говорили ранее, глядя на него, не скажешь, что данное уравнение является линейным, но нам необходимо раскрыть скобки и осуществить тождественные преобразования. Так что начнем!
Для начала вспоминаем формулы сокращенного умножения, в частности, квадрат суммы и квадрат разности.
Если ты не помнишь, что это такое и как раскрываются скобки, настоятельно рекомендую почитать тему «Формулы сокращенного умножения», так как эти навыки пригодятся тебе при решении практически всех примеров, встречающихся на экзамене.
Раскрыл? Сравниваем:
\( \displaystyle \begin{array}{l}{{\left( {x}-6 \right)}^{2}}+{{\left( x+3 \right)}^{2}}=2{{x}^{2}}\\{{x}^{2}}+36-12x+{{x}^{2}}+9+6x=2{{x}^{2}}\end{array}\)
Теперь пришло время привести подобные слагаемые. Помнишь, как нам в тех же начальных классах говорили «не складываем мухи с котлетами»? Вот напоминаю об этом.
Складываем все отдельно – множители, у которых есть \( \displaystyle {{x}^{2}}\), множители, у которых есть \( \displaystyle x\) и остальные множители, в которых нет неизвестных.
Как приведешь подобные слагаемые, перенеси все неизвестные влево, а все, что известно, – вправо. Что у тебя получилось?
\( \displaystyle \begin{array}{l}{{\left( {x}-6 \right)}^{2}}+{{\left( x+3 \right)}^{2}}=2{{x}^{2}}\\2{{x}^{2}}-2{{x}^{2}}-12x+6x+36+9=0\\-6x=-45\end{array}\)
Как ты видишь, иксы в квадрате исчезли, и здесь совершенно обычное линейное уравнение. Осталось только найти \( \displaystyle x\)!
\( \displaystyle x=\frac{-45}{-6}=7,5\)
И напоследок скажу еще одну очень важную вещь про тождественные преобразования.
Общие правила тождественных преобразований (или как упростить выражение)
Тождественные преобразования применимы не только для линейных уравнений, но и для квадратных, дробных рациональных и других.
Просто нужно запомнить, что…
При переносе множителей через знак равенства мы меняем знак на противоположный, а при делении или умножении на какое-то число мы умножаем/делим обе части уравнения на одно и то же число.
Что еще ты вынес из этого примера?
Что глядя на уравнение не всегда можно прямо и точно определить, является ли оно линейным или нет. Необходимо сначала полностью упростить выражение, и лишь потом судить, каким оно является.
Линейные уравнения. Примеры
Вот тебе еще пару примеров для самостоятельной тренировки – определи, является ли уравнение линейным и, если да, найди его корни:
- \( \displaystyle {{\left( {x}-2 \right)}^{2}}+{{\left( {x}-3 \right)}^{2}}=2{{x}^{2}}-7\)
- \( \displaystyle {{\left( 2{x}-4 \right)}^{2}}+3{{x}^{2}}+17={{\left( 3{x}-3 \right)}^{2}}\)
- \( \displaystyle \frac{6-x}{{{x}^{2}}+1}+\frac{5+6{{x}^{2}}}{3\left( {{x}^{2}}+1 \right)}=\frac{4{{x}^{2}}-2}{2\left( {{x}^{2}}+1 \right)}\)
Ответы:
1. Является.
\( \displaystyle \begin{array}{l}{{\left( {x}-2 \right)}^{2}}+{{\left( {x}-3 \right)}^{2}}=2{{x}^{2}}-7\\{{x}^{2}}+4-4x+{{x}^{2}}+9-6x=2{{x}^{2}}-7\\2{{x}^{2}}-10x+13=2{{x}^{2}}-7\\-10x=-20\\x=2\end{array}\)
2. Не является.
\( \displaystyle {{\left( 2{x}-4 \right)}^{2}}+3{{x}^{2}}+17={{\left( 3{x}-3 \right)}^{2}}\)
Раскроем скобки и приведем подобные слагаемые:
\( \displaystyle \begin{array}{l}4{{x}^{2}}+16-16x+3{{x}^{2}}+17=9{{x}^{2}}+9-18x\\7{{x}^{2}}-16x+33=9{{x}^{2}}+9-18x\\2{{x}^{2}}-2{x}-24=0\end{array}\)
Произведем тождественное преобразование – разделим левую и правую часть на \( \displaystyle 2\):
\( \displaystyle {{x}^{2}}-{x}-12=0\)
Мы видим, что уравнение не является линейным, так что искать его корни не нужно.
3. Является.
\( \displaystyle \begin{array}{l}\frac{6-x}{{{x}^{2}}+1}+\frac{5+6{{x}^{2}}}{3\left( {{x}^{2}}+1 \right)}=\frac{4{{x}^{2}}-2}{2\left( {{x}^{2}}+1 \right)}\\\frac{6\cdot \left( 6-x \right)}{6\cdot \left( {{x}^{2}}+1 \right)}+\frac{2\cdot \left( 5+6{{x}^{2}} \right)}{6\left( {{x}^{2}}+1 \right)}=\frac{3\left( 4{{x}^{2}}-2 \right)}{6\left( {{x}^{2}}+1 \right)}\\\frac{36-6x}{6\cdot \left( {{x}^{2}}+1 \right)}+\frac{10+12{{x}^{2}}}{6\left( {{x}^{2}}+1 \right)}=\frac{12{{x}^{2}}-6}{6\left( {{x}^{2}}+1 \right)}\end{array}\)
Произведем тождественное преобразование – умножим левую и правую часть на \( \displaystyle 6\left( {{x}^{2}}+1 \right)\ne 0\), чтобы избавиться от знаменателя.
Подумай, почему так важно, чтобы \( \displaystyle 6\left( {{x}^{2}}+1 \right)\ne 0\)?
Если ты знаешь ответ на этот вопрос, переходим к дальнейшему решению уравнения, если нет – обязательно загляни в тему «ОДЗ — область допустимых значений», чтобы не наделать ошибок в более сложных примерах.
Кстати, как ты видишь, ситуация, когда \( \displaystyle 6\left( {{x}^{2}}+1 \right)=0\) невозможна. Почему?
Итак, продолжаем и преобразовываем уравнение:
\( \displaystyle 36+6x+10+12{{x}^{2}}=12{{x}^{2}}-6\)
\( \displaystyle \begin{array}{l}36-6x+10+12{{x}^{2}}=12{{x}^{2}}-6\\-6x=-46-6\\-6x=-52\\x=\frac{-52}{-6}=8\frac{2}{3}\end{array}\)
Если ты без труда со всем справился, поговорим о линейных уравнениях с двумя переменными.
Линейные уравнения с двумя переменными
Теперь перейдем к чуть более сложному – линейным уравнениям с двумя переменными.
Линейные уравнения с двумя переменными имеют вид:
\( \displaystyle ax+by+c=0\), где \( \displaystyle a\), \( \displaystyle b\) и \( \displaystyle c\) – любые числа и \( \displaystyle a\ne 0\).
Как ты видишь, вся разница только в том, что в уравнение добавляется еще одна переменная. А так все то же самое – здесь нет иксов в квадрате, нет деления на переменную и т.д. и т.п.
Какой бы привести тебе жизненный пример… Возьмем того же Васю. Допустим, он решил, что каждому из 3-ех друзей он даст одинаковое количество яблок, а \( \displaystyle 2\) яблока оставит себе.
Сколько яблок нужно купить Васе, если каждому другу он даст по \( \displaystyle 1\) яблоку? А по \( \displaystyle 2\)? А если по \( \displaystyle 3\)?
Зависимость количества яблок, которое получит каждый человек к общему количеству яблок, которое необходимо приобрести будет выражена уравнением:
\( \displaystyle y=3x+2\), где
- \( \displaystyle x\) – количество яблок, которое получит \( \displaystyle 1\) человек (\( \displaystyle 1\), или \( \displaystyle 2\), или \( \displaystyle 3\));
- \( \displaystyle 2\) – количество яблок, которое Вася возьмет себе;
- \( \displaystyle y\) – сколько всего яблок нужно купить Васе с учетом количества яблок на человека.
Решая эту задачу, мы получим, что если одному другу Вася даст \( \displaystyle 1\) яблоко, то ему необходимо покупать \( \displaystyle 5\) штук, если даст \( \displaystyle 2\) яблока – \( \displaystyle 8\) и т.д.
И вообще. У нас две переменные. Почему бы не построить эту зависимость на графике?
Строим и отмечаем значение наших \( \displaystyle x\), то есть точки, с координатами \( \displaystyle 1\), \( \displaystyle 2\) и \( \displaystyle 3\)!
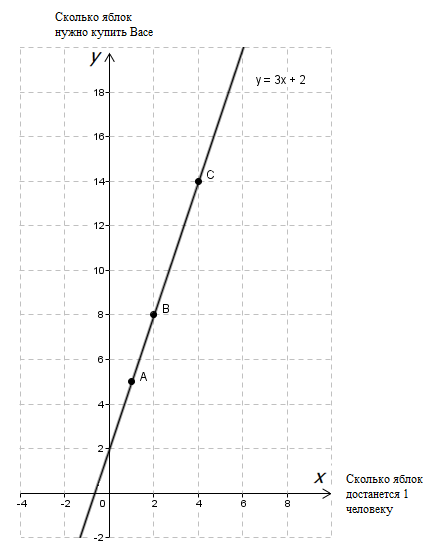
Как ты видишь, \( \displaystyle x\) и \( \displaystyle y\) зависят друг от друга линейно, отсюда и название уравнений – «линейные».
Графическое изображение линейных и нелинейных уравнений
Абстрагируемся от яблок и рассмотрим графически различные уравнения. Посмотри внимательно на два построенных графика – прямой и параболы, заданными произвольными функциями:
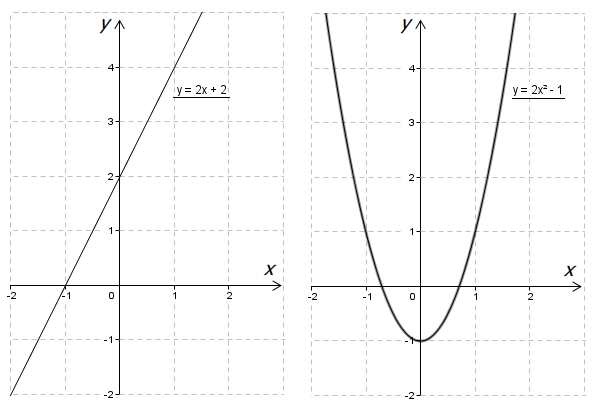
Найди и отметь на обоих рисунках точки \( \displaystyle x\), соответствующие \( \displaystyle y=2\).
Что у тебя получилось?
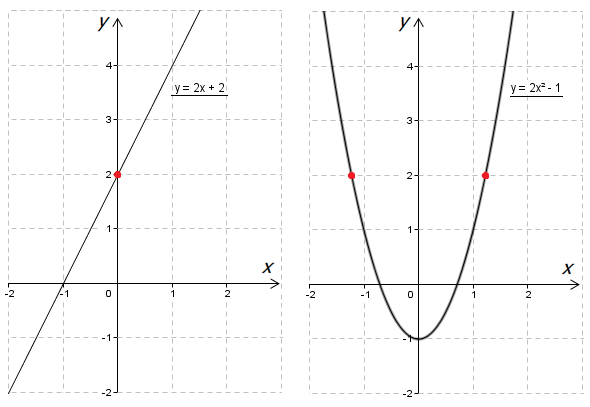
Ты видишь, что на графике первой функции одному \( \displaystyle y\) соответствует один \( \displaystyle x\).
То есть \( \displaystyle y\) и \( \displaystyle x\) линейно зависят друг от друга, что не скажешь про вторую функцию.
Конечно, ты можешь возразить, что на втором графике \( \displaystyle y=-1\) так же соответствует \( \displaystyle 1\) икс – \( \displaystyle x=0\) , но это только одна точка, то есть частный случай, так как ты все равно можешь найти такой \( \displaystyle y\), которому соответствует не только один \( \displaystyle x\).
Да и построенный график никак не напоминает линию, а является параболой.
Повторюсь, еще раз:
Графиком линейного уравнения должна быть прямая линия.
С тем, что уравнение не будет линейным, если у нас идет \( \displaystyle x\) в какой-либо степени – это понятно на примере параболы, хотя для себя ты можешь построить еще несколько простых графиков, например \( \displaystyle y={{x}^{3}}\) или \( \displaystyle y={{x}^{4}}\).
Но я тебя уверяю – ни один из них не будет представлять собой ПРЯМУЮ ЛИНИЮ.
Не веришь? Построй, а затем сравни с тем, что получилось у меня:
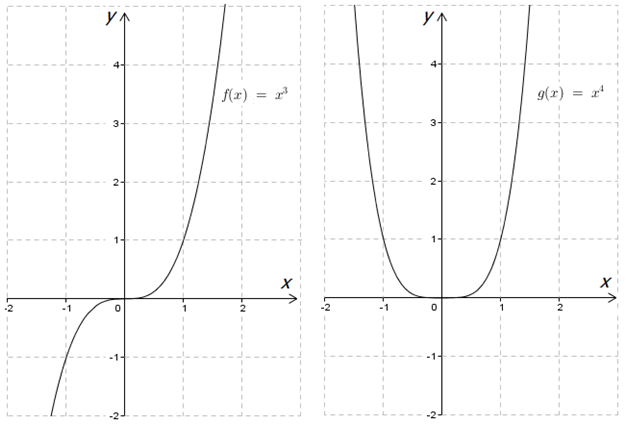
А что будет, если мы разделим что-то на \( \displaystyle x\), например, какое-то число? Будет ли линейная зависимость \( \displaystyle y\) и \( \displaystyle x\)?
Не будем рассуждать, а будем строить! Например, построим график функции \( \displaystyle y=\frac{1}{x}\).
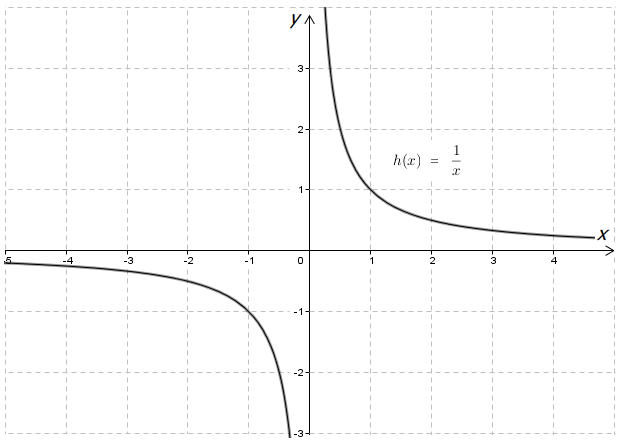
Как-то не выглядит построенное прямой линией… соответственно, уравнение не линейное.
Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
Линейные уравнения. 65 решенных уравнений.
Приёмы, которые мы узнаем в этом видео, применяются не только в линейных, но во всех типах уравнений, от квадратных до логарифмических.
Все приёмы будем разбирать на конкретных примерах и сразу же отрабатывать.
Мы решим разберём все возможные типы линейных уравнений, решив 65 уравнений.
Мы научимся:
- приводить подобные слагаемые
- «переносить» слагаемые через знак равно
- избавляться от коэффициентов (и заодно узнаем, что это такое – коэффициент:)
- раскрывать скобки (в том числе, если перед скобками минус)
- справляться с дробями в уравнениях
ЕГЭ 15. Показательные уравнения и неравенства. Сравнение чисел. Логарифмы
В этом видео мы научимся решать сложные показательные уравнения и показательные неравенства. Чаще всего они сводятся к квадратным или рациональным.
В сложных неравенствах нам никто не гарантирует, что концы интервалов получатся «красивыми» — частенько там возникают логарифмы.
Поэтому, чтобы знать, как эти точки располагаются на числовой прямой, нам необходимо уметь сравнивать значения логарифмов (друг с другом и с «обычными» числами).
Это мы также научимся делать.
ЕГЭ 13а. Решение тригонометрических уравнений
В этом видео вы увидите разбор одного из наиболее типичных для ЕГЭ тригонометрических уравнений (задача 13а). Вот какие темы мы разберем:
- 00:00 Введение. Простейшие тригонометрические уравнения. Стандартное решение. Арккосинус и арксинус
- 04:38 Решение тригонометрического уравнения (пункт а)
- 08:11 Нахождение всех корней тригонометрического уравнения, принадлежащих отрезку (пункт б)
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Спасибо огромное вам за ваш сайт, я просмотрела действительно огромное количество разных сайтов по подготовке по математике, но именно ваш сайт очень доходчиво объясняет материал а также в случае если какая-то тема до этого была упущена оставляется ссылка на прошлую тему. Удачи!
Соня, спасибо! Да, наша цель — сделать математику понятной:)