Свойства медианы треугольника
Привет!
Сегодня мы рассмотрим часть треугольника, которая не раз поможет тебе при решении многих задач, — медиану.
Эта приятная, лёгкая и полезная теория!
Поехали!
Медиана треугольника — коротко о главном
Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
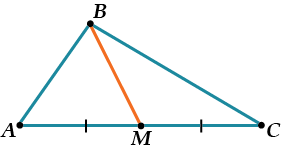
Медиана делит площадь треугольника пополам
Но \( \displaystyle AM=CM\), значит, \( \displaystyle {{S}_{\triangle ABM~}}={{S}_{\triangle BMC~}}\)
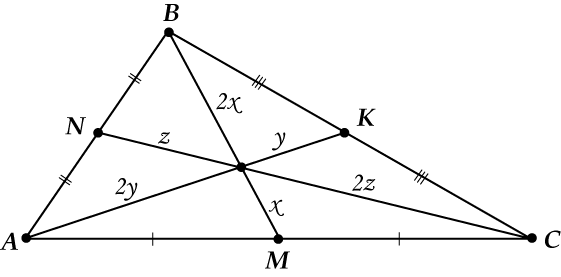
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины.
Но \( \displaystyle AM=CM\), значит, \( \displaystyle {{S}_{\triangle ABM~}}={{S}_{\triangle BMC~}}\)
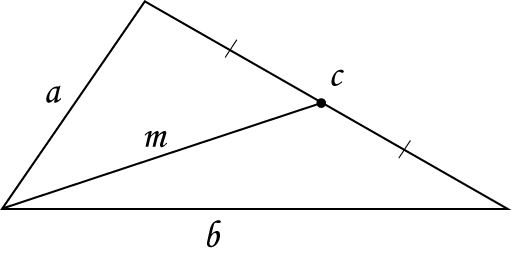
Длина медианы: \( \displaystyle {{m}^{2}}=\frac{1}{4}~\left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} \right)\)
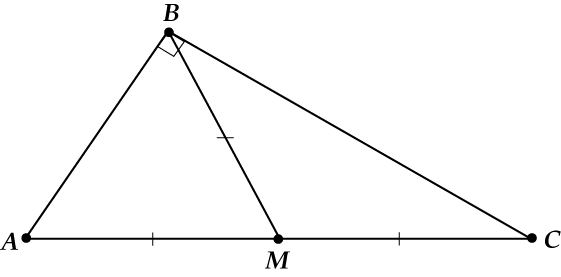
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
и наоборот…
Если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.
Определение медианы треугольника
Это очень просто! Возьми треугольник.
Отметь на какой-нибудь его стороне середину \( \displaystyle M\).
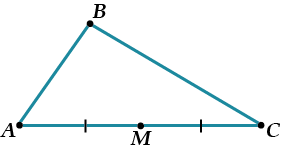
И соедини с противоположной вершиной!

Получившийся отрезок \( \displaystyle BM\) и есть медиана.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медиана в прямоугольном треугольнике
Медиана равна половине гипотенузы прямоугольного треугольника!
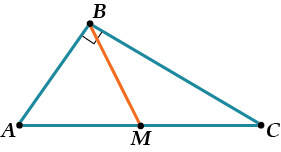
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.
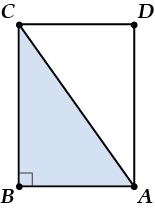
Ты заметил, что наш треугольник \( \displaystyle ABC\) – ровно половина этого прямоугольника?
Проведём диагональ \( \displaystyle BD\):
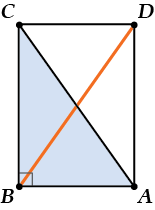
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?
Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»
Но одна из диагоналей – \( \displaystyle AC\) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы \( \displaystyle \Delta ABC\).
Она называлась у нас \( \displaystyle M\).
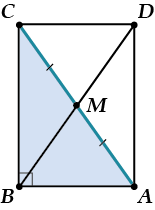
Значит, половина второй диагонали – наша медиана \( \displaystyle BM\). Диагонали равны, их половинки, конечно же, тоже. Вот и получим \( \displaystyle BM=MA=MC\)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?
Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
Решение задач на свойства медианы в прямоугольном треугольнике
Давай посмотрим, как это свойство помогает решать задачи.
Задача №1:
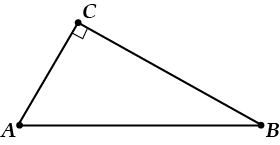
В \( \displaystyle \Delta ABC\) стороны \( \displaystyle AC=5\); \( \displaystyle BC=12\). Из вершины \( \displaystyle C\) проведена медиана \( \displaystyle CN\).
Найти \( \displaystyle AB\), если \( \displaystyle AB=2CN\).
Рисуем:
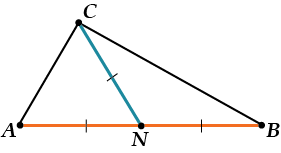
Сразу вспоминаем, это если \( \displaystyle CN=\frac{AB}{2}\), то \( \displaystyle \angle ACB=90{}^\circ \)!
Ура! Можно применить теорему Пифагора!
Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
Ответ: \( AB=13\)
А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении \( 2:1\), считая от вершины.
Сложно? Смотри на рисунок:
Медианы \( \displaystyle AM\), \( \displaystyle BN\) и \( \displaystyle CK\) пересекаются в одной точке.
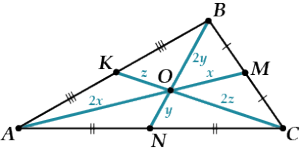
Запомни:
- \( \displaystyle AO\) – вдвое больше, чем \( \displaystyle OM\);
- \( \displaystyle BO\) – вдвое больше, чем \( \displaystyle ON\);
- \( \displaystyle CO\) – вдвое больше, чем \( \displaystyle OK\).
Задача №2:
В треугольнике \( \displaystyle ABC\) проведены медианы \( \displaystyle BM\) и \( \displaystyle AK\), которые пересекаются в точке \( \displaystyle O\). Найти \( \displaystyle BO\), если \( \displaystyle AB=3;\text{ }BC=4,\text{ }\angle B=90{}^\circ .\)
Решение:
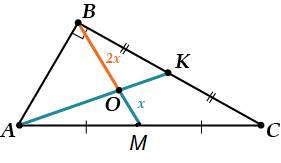
\( \displaystyle \angle B=90{}^\circ \) – треугольник прямоугольный!
Значит, \( BM=\frac{AC}{2}\).
(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).
Найдём \( \displaystyle AC\) по теореме Пифагора:
Теорема о медиане и площади треугольника
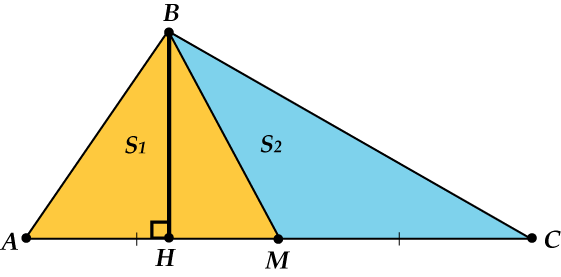
Медиана делит площадь треугольника пополам
Почему? А давай вспомним самую простую форму площади треугольника. \( S=\frac{1}{2}a~\cdot h\).
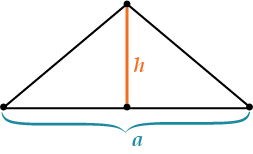
И применим эту формулу аж два раза!
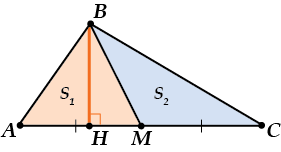
Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).
Но! Высота-то у них одна и та же – \( \displaystyle BH\)!
Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).
Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу
\( S=\frac{1}{2}a~\cdot h\).
1) B \( \displaystyle \triangle ABM\):
| «\( \displaystyle a\)» – это \( \displaystyle AM\) «\( \displaystyle h\)» – это \( \displaystyle BH\) | \( \displaystyle \Rightarrow {{S}_{\triangle ABM}}=\frac{1}{2}~AM~\cdot BH\) |
2) B \( \displaystyle \triangle BMC\):
| «\( \displaystyle a\)» – это \( \displaystyle CM\) «\( \displaystyle h\)» – это опять \( \displaystyle BH\) | \( \displaystyle \Rightarrow {{S}_{\triangle BMC}}=\frac{1}{2}~CM~\cdot BH\) |
Запишем ещё раз:
Теорема о трех медианах треугольника
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины.
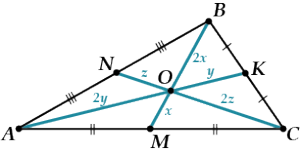
Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
1. Медианы треугольника пересекаются в одной точке.
2. Точкой пересечения медианы делятся в отношении \( \displaystyle 2:1\ \), считая от вершины.
Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.
Доказательство теоремы о трех медианах треугольника
Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой \( \displaystyle E\).
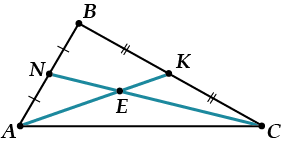
Соединим точки \( \displaystyle N\) и \( \displaystyle K\). Что получилось?

Конечно, \( \displaystyle NK\) – средняя линяя \( \displaystyle \triangle ABC\). Ты помнишь, что это значит?
- \( \displaystyle NK\) параллельна \( \displaystyle AC\);
- \( \displaystyle NK=\frac{AC}{2}\).
А теперь проведем ещё одну среднюю линию: отметим середину \( \displaystyle AE\) – поставим точку \( \displaystyle F\), отметим середину \( \displaystyle EC\) — поставим точку \( \displaystyle G\).
Теперь \( \displaystyle FG\) – средняя линия \( \displaystyle \triangle AEC\). То есть:
- \( \displaystyle FG\) параллельна \( \displaystyle AC\);
- \( \displaystyle FG=\frac{AC}{2}\).
Заметил совпадения? И \( \displaystyle NK\) , и \( \displaystyle FG\) – параллельны \( \displaystyle AC\). И \( \displaystyle NK=\frac{AC}{2}\), и \( \displaystyle FG=\frac{AC}{2}\).
Что из этого следует?
- \( \displaystyle NK\) параллельна \( \displaystyle FG\);
- \( \displaystyle NK=FG\)
Посмотри теперь на четырехугольник \( \displaystyle NKGF\). У какого четырехугольника противоположные стороны (\( \displaystyle NK\) и \( \displaystyle FG\)) параллельны и равны?
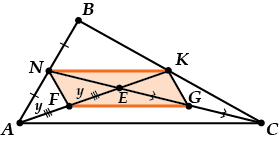
Конечно же, только у параллелограмма!
Значит, \( \displaystyle NKGF\) – параллелограмм. Ну и что?
А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
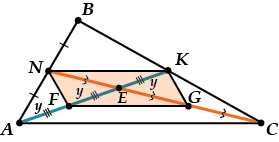
Получилось что:
Формула длины медианы треугольника
Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно?
Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем.
Итак, \( \displaystyle {{m}^{2}}=\frac{1}{4}~\left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} \right)\)

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам
Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно.
Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.
Как с этим справиться?
Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать.
ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники.
ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия
Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше.
И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ №16. Подобие треугольников. Задачи н доказательство
Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Бакыт
26 марта 2018
Очень полезно! Теперь я понял, как доказать, что медиана, проведенная к гипотенузе, равна половине этой же гипотенузы. Спасибо за объяснение, оно очень подробное и легкое!
Алмаз
22 апреля 2018
Спасибо вам большое, раньше не хотел учить, но теперь понял что пригодиться. Вернул утраченные знания!
Диана
13 ноября 2019
Все рассказано не сухим геометрическим доказательством, а реально с юмором. Подходит для закрепления информации
Деннкафф
03 апреля 2020
Спс очень доступно и полезно рассказал!