Параллелепипед
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Так и есть.
Читай статью, смотри вебинар и ты все про него будешь знать!
Параллелепипед — коротко о главном
Параллелепипед — это четырехугольная призма (многогранник с \( \displaystyle 6\) гранями), все грани которой — параллелограммы.
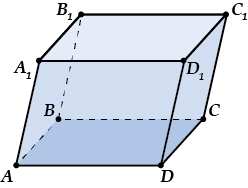
Прямой параллелепипед —это параллелепипед, у которого \( \displaystyle 4\) боковые грани — прямоугольники.
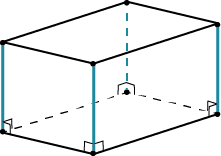
Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники
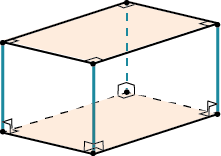
Куб — параллелепипед, у которого все грани квадраты.

Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства параллелепипеда
- Противолежащие грани параллелепипеда параллельны и равны.
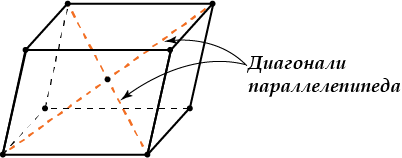
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений. \( \displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}\).

Параллелепипед — подробнее
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.

Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Далее смотри на картинки, запоминай и не путай!
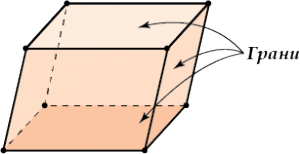
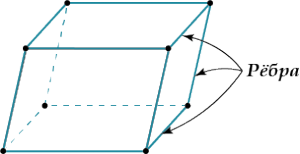

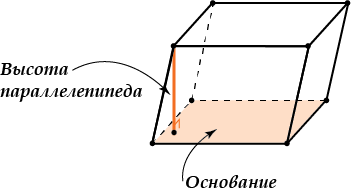

Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
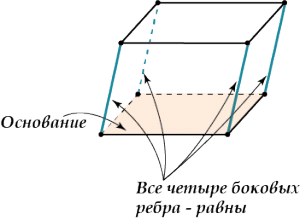
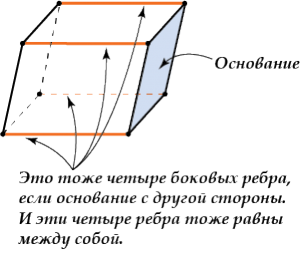
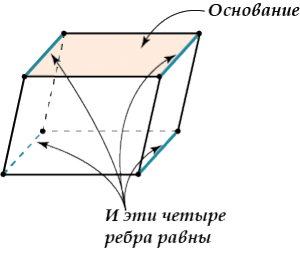
Та грань, на которую опущена высота, называется основанием.
Свойства параллелепипеда
- Все грани параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.
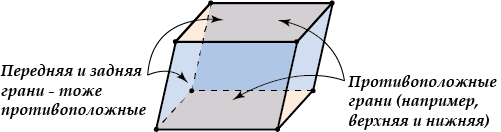
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.
- Боковые ребра параллелепипеда равны.
- Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
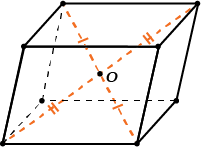
Прямой параллелепипед
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:

У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольный параллелепипед
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

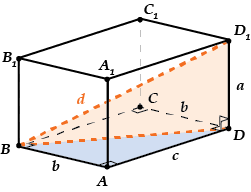
Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.\( \displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}\).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:
Куб
Куб – параллелепипед, у которого все грани квадраты.

Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
\( \displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}\),
То есть
\( \displaystyle d=a\sqrt{3}\)Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна \( \displaystyle 5\sqrt{3}\). Найти полную поверхность».
Решим ее.
Бонус. Видео из нашего курса по подготовке к ЕГЭ по математике
А теперь пора закрепить знания и порешать задачки. Иначе твои знания будут не полными!
На этом вебинаре мы на примере самых простых объемных фигур (куб, параллелепипед, призма — задание №8 из ЕГЭ) научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Бери ручку, тетрадь и решай задачи вместе с Алексеем!
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Скажите , пожалуйста, если разрезать куб на две равные половинки, как будет называться такая половинка-прямоугольный параллелепипед? Спасибо за такое наглядное очень подробное описание. Буду на досуге вдумчиво читать, разбираться
Наталья, зависит от того, как разрезать. Если разрез сделать параллельно граням, тогда да, прямоугольный параллелепипед.
Но если, например, разрезать по диагоналям двух противоположных граней («наискосок»), получатся треугольные призмы (и они тоже будут равными половинками). И таких способов разрезать очень много — главное, чтобы разрез проходил через центр куба.
Здравствуйте, Алексей!
Благодарю Вас!!! Вы можете посоветовать такой учебник для детей, где
наглядно и очень доступно были бы объяснены все эти объемные и плоские фигуры?
Всего доброго! С уважением, Наталья
Огромное вам СПАСИБО !всё понятно и интересно объяснили,спасибо,было такое ощущение,что вы рядом .
Спасибо, Левани!
Некоторые комментарии прошлых лет к этой статье:
Пульхерия Алексеевна
11 мая 2018
Спасибо огромное!!!!! Вы такая потрясающая женщина!!! Как вам это удалось????
Аноним
05 июня 2018
Прекрасная статья, большое спасибо!
Саша
09 января 2019
Шикарное объяснение! Спасибо!
Ольга
21 января 2019
Вот бы в школе так объясняли.!!! Всё по полочкам разложено. Спасибо!
гузаль
12 июня 2019
спасибо! все было понятно. И за мотивацию тоже спасибо)))