Параллельность прямых, прямой и плоскости и параллельность плоскостей в пространстве
Помнишь, на плоскости была тема «Параллельные прямые»?
Так вот, в пространстве тоже бывают параллельные прямые.
Но… всё немного иначе.
А еще есть параллельность плоскостей – очень важная штука в стереометрии.
Умея с ней работать, становится легче находить углы и значения величин в задачах, выполнять правильные построения.
Читай статью и будешь знать о параллельности плоскостей все!
Параллельность прямых в пространстве
Определение
Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Вот так:
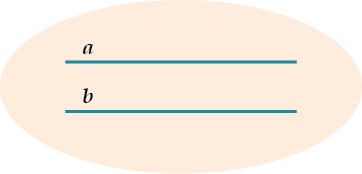
Обрати внимание! Здесь очень важны слова «лежат в одной плоскости».
Потому что в пространстве бывают другие, НЕ параллельные прямые, которые тоже НЕ пересекаются. Вот, например, такие:
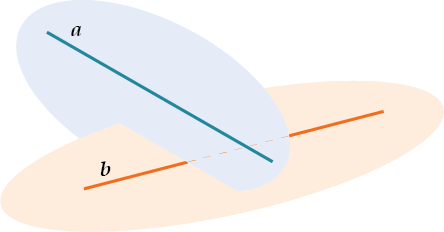
Видишь, через прямые \( \displaystyle a\) и \( \displaystyle b\) никак нельзя провести плоскость, но они и не пересекаются.
Такие прямые называются скрещивающиеся.
Не пересекающиеся! И не параллельные!
Итак, ещё раз:
Прямые в пространстве параллельны, если лежат в одной плоскости и не пересекаются.
Признаки параллельности прямых в пространстве
Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
Если в одной из пересекающихся плоскостей лежит прямая, параллельная другой плоскости, то она параллельна линии пересечения плоскостей.
Пример на признак параллельности прямых в пространстве
Пусть плоскости \( \displaystyle ABDC\) и \( \displaystyle CDFE\).
\( \displaystyle AB\parallel EF\), значит, \( \displaystyle AB\parallel CD\) по признаку параллельности прямых в пространстве.
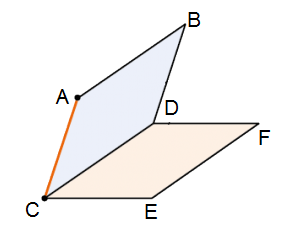
Параллельность прямой и плоскости
Определение параллельности прямой и плоскости
Прямая и плоскость параллельны, если они не пересекаются, сколько бы их ни продолжали.

Вот так: видишь, прямая как бы «висит» над плоскостью.
И представь себе, существует признак параллельности прямой и плоскости. Давай его сформулируем.
Признак параллельности прямой и плоскости

Прямая \(\displaystyle a \) параллельна плоскости \(\displaystyle \alpha \), если в этой плоскости есть (хоть одна!) прямая \(\displaystyle b \), параллельная \(\displaystyle a \).
Можно сказать и немного другими словами, но смысл остаётся тот же.
Если прямая \(\displaystyle a \) параллельна прямой \(\displaystyle b\), лежащей в плоскости \(\displaystyle \alpha\), то прямая \(\displaystyle a \) параллельна и всей плоскости \(\displaystyle \alpha \).
Пример на признак параллельности прямой и плоскости
Пусть \(\displaystyle SABCD\) – правильная 4 — угольная пирамида.
Тогда, например, \(\displaystyle AB \parallel SCD\). Почему? Но ведь \(\displaystyle AB \parallel CD\), а \(\displaystyle CD \) лежит в плоскости \(\displaystyle SCD\).

Значит (по признаку) \(\displaystyle AB \parallel SCD\).
Параллельность плоскостей
Определение параллельности плоскостей
Плоскости называются параллельными, если они не пересекаются, сколько бы их не продолжали
И так же, как для прямой и плоскости, есть признак параллельности плоскостей. Его формулировка немного длиннее.
Признак параллельности двух плоскостей
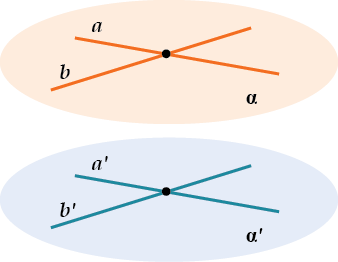
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.
Слишком много слов? А ты посмотри на картинку: если \( \displaystyle a \parallel {a}’\) и \( \displaystyle b \parallel {b}’\), то это значит, что \( \displaystyle \alpha \) и \( \displaystyle {{\alpha }’}\) (плоскости) — параллельны, то есть нигде не пересекутся.
Параллельность в пространстве: свойство транзитивности
Ух, ну и название! О чём же мы?
А вот ты задумайся над вопросом: правда ли, что если прямая \( \displaystyle a \) параллельна прямой \( \displaystyle b\), a \( \displaystyle b \parallel c\), то \( \displaystyle a \parallel c\)?
И есть ответ: правда! И как раз такой перенос с “\( \displaystyle a\)” через “\( \displaystyle b\)” на “\( \displaystyle c\)” и называется «транзитивность».
Давай-ка теперь рассмотрим несколько вариантов в буквах и картинках:
\( \displaystyle a \parallel b\) и \( \displaystyle b \parallel c \Rightarrow a \parallel c\).
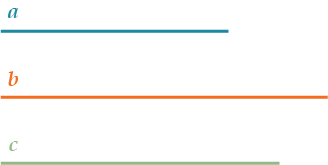
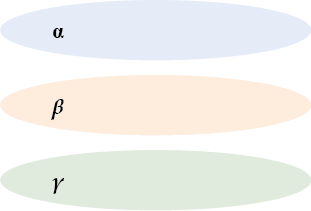
\( \displaystyle \alpha \parallel \beta\) и \( \displaystyle \beta \parallel \gamma \Rightarrow \alpha \parallel \gamma\).
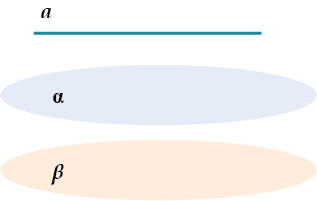
\( \displaystyle a\parallel \alpha\quad\) и \( \displaystyle \quad \alpha\parallel \beta\Rightarrow a\parallel \beta\).
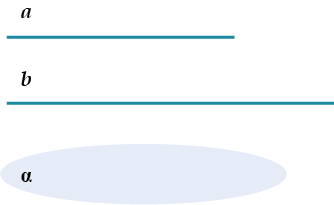
\( \displaystyle \alpha \parallel b\quad\) и \( \displaystyle\quad b\parallel \alpha \Rightarrow text{a}\parallel \alpha \)
И один неверный вариант:
\( \displaystyle a\parallel \alpha \) и \( \displaystyle \alpha \parallel b\) \( \displaystyle НЕ \Rightarrow \) \( \displaystyle a\parallel b\).
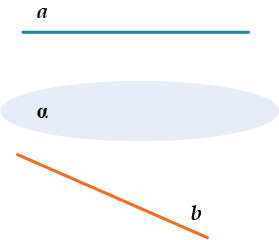
Посмотри – убедись!
Ну вот, мы обсудили определения и признаки параллельности прямых и плоскостей и даже немножко порисовали транзитивности. Давай теперь рассмотрим несколько примеров.
Пример на признак параллельности плоскостей
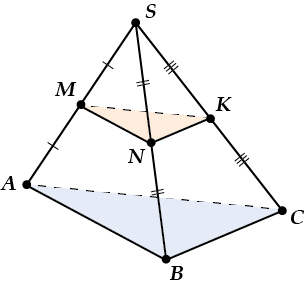
Пусть в пирамиде \( \displaystyle SABC\) проведена плоскость \( \displaystyle MNK\) через середины рёбер \( \displaystyle SA\), \( \displaystyle SB\) и \( \displaystyle SC\).
Тогда \( \displaystyle MNK\parallel ABC\). Почему?
Да просто \( \displaystyle MN\parallel AB\) (средняя линия), \( \displaystyle NK\parallel BC\) (тоже средняя линия, но в \( \displaystyle \Delta SBC\)).
Значит, получилось, что \( \displaystyle MN\) и \( \displaystyle NK\) – пересекающиеся прямые в одной плоскости соответственно параллельны \( \displaystyle AB\) и \( \displaystyle BC\) – пересекающимся прямым в другой плоскости – работает признак \( \displaystyle \Rightarrow \) \( \displaystyle MNK\parallel ABC\).
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Спасибо! Все понятно, доходчиво.
Спасибо, Валентина. Рады, что понравилось!
Некоторые комментарии прошлых лет к этой статье:
Валерия
04 декабря 2019
Полезный и хороший материал !
Александр (админ)
04 декабря 2019
Спасибо, Валерия!