Перпендикулярность прямой и плоскости
В пространстве перпендикулярными могут быть:
- две прямые
- прямая и плоскость
- две плоскости
Давай для полного понимания рассмотрим не только перпендикулярность прямой и плоскости, а все три случая перпендикулярности в пространстве.
Все относящиеся к ним определения и формулировки теорем.
А потом обсудим очень важную теорему о трёх перпендикулярах.
И ты будешь знать о перпендикулярности в пространстве все!
Поехали!
Перпендикулярность в пространстве — коротко о главном
Перпендикулярность двух прямых
Две прямые в пространстве перпендикулярны, если угол между ними \( 90{}^\circ \).
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.
Перпендикулярность плоскостей
Плоскости перпендикулярны, если двугранный угол между ними равен \( 90{}^\circ \).
Критерий перпендикулярности плоскостей
Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.
Теорема о трех перпендикулярах
Прямая \( a\), не лежащая в плоскости \( \alpha \), перпендикулярна прямой \( b\), лежащей в плоскости \( \alpha \), тогда и только тогда, когда проекция \( a\prime \) прямой a перпендикулярна прямой \( b\).
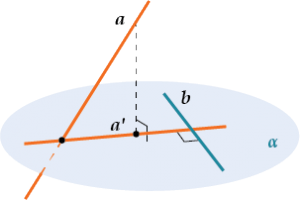
Перпендикулярность двух прямых
Определение:
Две прямые в пространстве перпендикулярны, если угол между ними \( \displaystyle 90{}^\circ \).
Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.
На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):

А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:
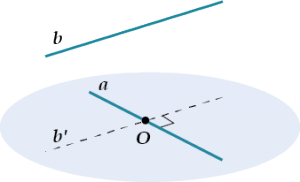
Прямая \( \displaystyle a\) перпендикулярна прямой \( \displaystyle b\), хотя и не пересекается с нею. Как так?
Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми \( \displaystyle a\) и \( \displaystyle b\), нужно через произвольную точку \( \displaystyle O\) на прямой a провести прямую \( \displaystyle {b}’\parallel b\).
И тогда угол между \( \displaystyle a\) и \( \displaystyle b\) (по определению!) будет равен углу между \( \displaystyle a\) и \( \displaystyle {{b}’}\).
Вспомнили? Ну вот, а в нашем случае – если окажутся перпендикулярны прямые \( \displaystyle a\) и \( \displaystyle {{b}’}\), то нужно считать перпендикулярными прямые \( \displaystyle a\) и \( \displaystyle b\).
Для полной ясности давай рассмотрим пример
Пусть есть куб \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\). И тебя просят найти угол между прямыми \( \displaystyle AC\) и \( \displaystyle {{B}_{1}}{{D}_{1}}\).
Эти прямые не пересекаются – они скрещиваются. Чтобы найти угол между \( \displaystyle AC\) и \( \displaystyle {{B}_{1}}{{D}_{1}}\), проведём \( \displaystyle BD\).
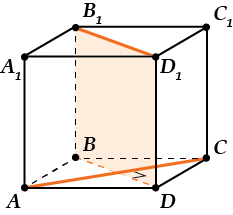
Из-за того, что \( \displaystyle B{{B}_{1}}{{D}_{1}}D\) — параллелограмм (и даже прямоугольник!), получается, что \( \displaystyle {{B}_{1}}{{D}_{1}}\parallel BD\).
А из-за того, что \( \displaystyle ABCD\) – квадрат, выходит, что \( \displaystyle AC\bot BD\). Ну, и значит \( \displaystyle AC\bot {{B}_{1}}{{D}_{1}}\).
Перпендикулярность прямой и плоскости
Определение:
Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.
Вот картинка:
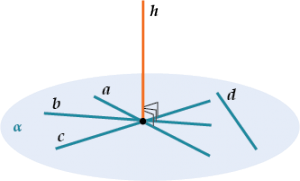
Прямая \( \displaystyle h\) перпендикулярна плоскости \( \displaystyle \alpha \), если она перпендикулярна всем-всем прямым в этой плоскости: и \( \displaystyle a\), и \( \displaystyle b\), и \( \displaystyle c\), и даже \( \displaystyle d\)!
И ещё миллиарду других прямых!
Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит!
Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости.
Формулируем:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Оцени, как здорово:
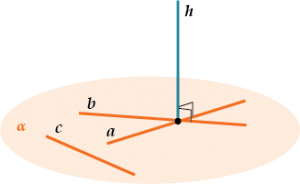
Если найдутся всего лишь две пересекающиеся прямые (\( \displaystyle a\) и \( \displaystyle b\)) в плоскости \( \displaystyle\alpha\), которым перпендикулярна прямая \( \displaystyle h\), то эта прямая сразу окажется перпендикулярна плоскости \( \displaystyle \alpha \),
То есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой \( \displaystyle c\)).
Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.

Что это за арка? Это значок «пересечение»! Хороший способ быстрее писать конспекты 🙂
Прямая перпендикулярна двум пересекающимся прямым!
И опять рассмотрим пример
Пусть нам дан правильный тетраэдр \( \displaystyle ABCD\).
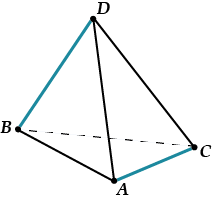
Задача: доказать, что \( \displaystyle BD\bot AC\).
Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!
А вот смотри:
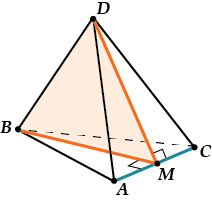
Давай отметим середину \( \displaystyle M\) ребра \( \displaystyle AC\) и проведём \( \displaystyle BM\) и \( \displaystyle DM\).
Это медианы в \( \displaystyle \Delta ABC\) и \( \displaystyle \Delta ADC\).
Треугольники – правильные \( \displaystyle \Rightarrow BM\bot AC\) и \( \displaystyle DM\bot AC\).
Вот оно, чудо: получается, что \( \displaystyle AC\bot BMD\), так как \( \displaystyle AC\bot BM\) и \( \displaystyle AC\bot DM\).
И далее, \( \displaystyle AC\bot BMD\Rightarrow AC\bot \) всем прямым в плоскости \( \displaystyle BMD\), а значит, и \( \displaystyle AC\bot BD\).
Доказали.
И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.
Перпендикулярность плоскостей
Определение:
Плоскости перпендикулярны, если двугранный угол между ними равен \( \displaystyle 90{}^\circ \).
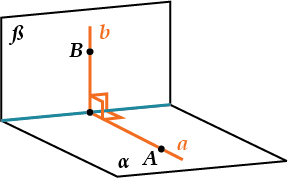
То есть (подробнее смотри в теме «двугранный угол») две плоскости (\( \displaystyle \alpha\) и \( \displaystyle \beta\)) перпендикулярны, если окажется, что угол между двумя перпендикулярами (\( \displaystyle a\) и \( \displaystyle b\)) к линии пересечения этих плоскостей равен \( \displaystyle 90{}^\circ \).
И есть теорема, которая связывает понятие перпендикулярных плоскостей с понятием перпендикулярность в пространстве прямой и плоскости.
Теорема эта называется: Критерий перпендикулярности плоскостей.
Критерий перпендикулярности плоскостей
Давай сформулируем:
Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.
Как всегда, расшифровка слов «тогда и только тогда» выглядит так:
- Если \( \displaystyle \alpha \bot \beta \), то \( \displaystyle \alpha \) проходит через перпендикуляр к \( \displaystyle \beta \).
- Если \( \displaystyle \alpha \) проходит через перпендикуляр к \( \displaystyle \beta \), то \( \displaystyle \alpha \bot \beta \).
(естественно, здесь \( \displaystyle \alpha \) и \( \displaystyle \beta \) — плоскости).
Теорема о трёх перпендикулярах
Эта теорема – одна из самых важных в стереометрии, но, к сожалению, и одна из самых непростых в применении.
Так что нужно быть очень внимательным!
Итак, формулировка:
Прямая \( \displaystyle a\), не лежащая в плоскости \( \displaystyle \alpha \), перпендикулярна прямой \( \displaystyle b\), лежащей в плоскости \( \displaystyle \alpha \), тогда и только тогда, когда проекция \( \displaystyle {{a}’}\) прямой a перпендикулярна прямой \( \displaystyle b\).
И снова расшифровка слов «тогда и только тогда». Теорема утверждает сразу две вещи (смотри на картинку):
- \( \displaystyle a\bot b\Rightarrow {a}’\bot b\)
- \( \displaystyle {a}’\bot b\Rightarrow a\bot b\).

Давай попробуем применить эту теорему для решения задачи.
Задача: дана правильная шестиугольная пирамида \( \displaystyle SABCDEF\). Найти угол между прямыми \( \displaystyle AS\) и \( \displaystyle CE\).
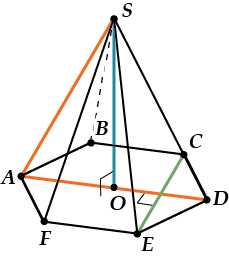
Решение:
Из-за того, что в правильной пирамиде вершина при проекции попадает в центр основания, оказывается, что прямая \( \displaystyle AD\) — проекция прямой \( \displaystyle AS\).
Но мы знаем, что в правильном шестиугольнике \( \displaystyle AD\bot CE\). Применяем теорему о трёх перпендикулярах:
\( \displaystyle AD\bot CE\Rightarrow AS\bot CE\)И пишем ответ: \( \displaystyle 90{}^\circ \).
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Очень грамотно и просто изложен материал. Рекомендую для повторения.
Спасибо, Ольга. Рады, что понравилось.