Правильные многогранники
Существует всего пять правильных многогранников:
- Тетраэдр
- Куб (Гексаэдр)
- Октаэдр
- Икосаэдр
- Додекаэдр
Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!
Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.
А также решим задачу №8.
О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».
Поехали!
Правильные многогранники — подробнее
Многогранник называется правильным, если:
- он выпуклый;
- все его грани являются правильными многоугольниками;
- в каждой его вершине сходится одинаковое число его ребер.
Пять правильных многогранников
Тетраэдр
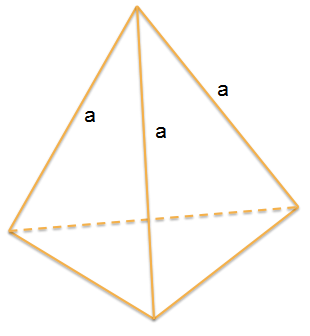
Тетраэдр состоит из четырёх равносторонних треугольников.
Фигура имеет 4 грани, 4 вершины и 6 ребер(a).
Площадь поверхности тетраэдра:
\( \displaystyle S={{a}^{2}}\sqrt{3}\)
Объем тетраэдра:
\( \displaystyle V=\frac{{{a}^{3}}}{12}\sqrt{2}\)
Радиус описанной вокруг тетраэдра сферы:
\( \displaystyle R=\frac{a}{4}\sqrt{6}\)
Радиус вписанной в тетраэдр сферы:
Куб (Гексаэдр)
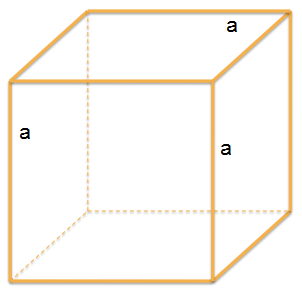
Куб состоит из шести квадратов.
Фигура имеет 6 граней, 8 вершин и 12 ребер (a).
Площадь поверхности куба:
\( \displaystyle S=6{{a}^{2}}\)
Объем куба:
\( \displaystyle V={{a}^{3}}\)
Радиус описанной вокруг куба сферы:
\( \displaystyle R=\frac{a}{2}\sqrt{3}\)
Радиус вписанной в куб сферы:
Октаэдр
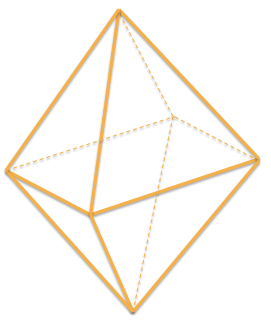
Октаэдр составлен из восьми равносторонних треугольников.
Фигура имеет 8 граней, 6 вершин и 12 ребер (a).
Площадь поверхности октаэдра:
\( \displaystyle S=2{{a}^{2}}\sqrt{3}\)
Объем октаэдра:
\( \displaystyle V=\frac{{{a}^{3}}}{3}\sqrt{2}\)
Радиус описанной вокруг октаэдра сферы:
\( \displaystyle R=\frac{a}{2}\sqrt{2}\)
Радиус вписанной в октаэдр сферы:
Икосаэдр
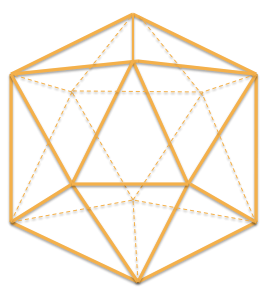
Икосаэдр составлен из двадцати равносторонних треугольников.
Фигура имеет 20 граней, 12 вершин и 30 ребер (a).
Площадь поверхности икосаэдра:
\( \displaystyle S=5{{a}^{2}}\sqrt{3}\)
Объем икосаэдра:
\( \displaystyle V=\frac{5{{a}^{3}}}{12}\left( 3+\sqrt{5} \right)\)
Радиус описанной вокруг икосаэдра сферы:
\( \displaystyle R=\frac{a}{4}\sqrt{2\left( 5+\sqrt{5} \right)}\)
Радиус вписанной в икосаэдр сферы:
Додекаэдр
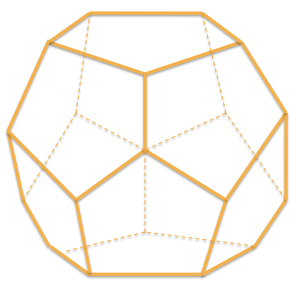
Додекаэдр составлен из двенадцати равносторонних пятиугольников.
Фигура имеет 12 граней, 20 вершин и 30 ребер (a).
Площадь поверхности додекаэдра:
\( \displaystyle S=3{{a}^{2}}\sqrt{5\left( 5+2\sqrt{5} \right)}\)
Объем додекаэдра:
\( \displaystyle V=\frac{{{a}^{3}}}{4}\left( 15+7\sqrt{5} \right)\)
Радиус описанной вокруг додекаэдра сферы:
\( \displaystyle R=\frac{a}{4}\left( 1+\sqrt{5} \right)\sqrt{3}\)
Радиус вписанной в додекаэдр сферы:
Решение задачи №8 на тему «Правильные многогранники»
Задача:
В кубе \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) с ребром \( \displaystyle \sqrt{12}\) найдите \( \displaystyle A{{C}_{1}}\).
Решение:
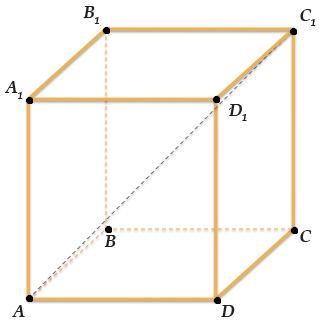
\( \displaystyle d=a\sqrt{3}\),
где \( \displaystyle d\) – диагональ куба,\( \displaystyle a\) – сторона куба.\( \displaystyle A{{C}_{1}}\) – это и есть диагональ куба.
Тогда \( \displaystyle A{{C}_{1}}=a\sqrt{3}=\sqrt{12}\cdot \sqrt{3}=\sqrt{36}=6\).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



ОТЛИЧНО ПОСТРОЕННАЯ СХЕМА ЧЕРТЕЖЕЙ СОГЛАСНО ФОРМУЛАМ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ ДЛЯ РЕШЕНИЯ ЭЛЕМЕНТАРНЫХ ЗАДАЧ