Определение расстояния между параллельными плоскостями

Расстояние между параллельными плоскостями – длина отрезка их общего перпендикуляра, заключенного между плоскостями

Вот так:

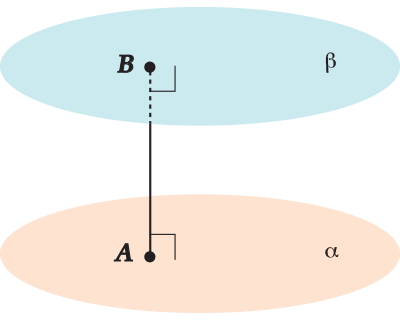
\( \displaystyle AB\) – расстояние между плоскостями.

Да, но как найти это расстояние в задачах?

Иногда бывает так, что по каким-то соображениям можно прямо увидеть этот общий перпендикуляр.

Вот, например:

Решение задачи №1

В кубе \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) найти расстояние между плоскостями \( \displaystyle {{A}_{1}}BD\) и \( \displaystyle {{B}_{1}}{{D}_{1}}{{C}_{1}}\), если ребро куба равно \( \displaystyle 1\).

В кубе \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) найти расстояние между плоскостями \( \displaystyle \ {{A}_{1}}BD\) и \( \displaystyle \ {{B}_{1}}{{D}_{1}}{{C}_{1}}\), если ребро куба равно \( \displaystyle 1\).

Решаем:

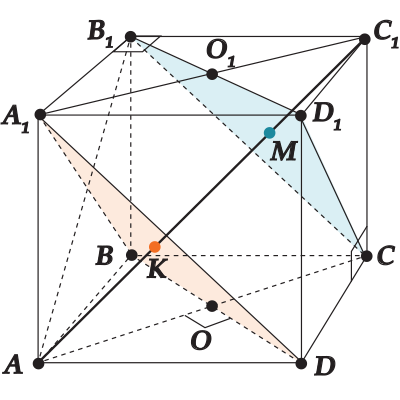
Проведем диагональ куба \( \displaystyle A{{C}_{1}}\).

Докажем, что \( \displaystyle A{{C}_{1}}\bot {{A}_{1}}BD\) (тогда будет и \( \displaystyle A{{C}_{1}}\bot B{{D}_{1}}C\))

1) \( \displaystyle C{{C}_{1}}\bot ABCD\rightarrow AC\) – проекция \( \displaystyle A{{C}_{1}}\) на \( \displaystyle ABCD\).

\( \displaystyle AC\bot BD\) т.к. (\( \displaystyle ABCD\) – квадрат), значит (Внимание!) по теореме о трех перпендикулярах \( \displaystyle A{{C}_{1}}\bot BD\)

2) \( \displaystyle {{C}_{1}}{{B}_{1}}\bot A{{A}_{1}}{{B}_{1}}B\rightarrow A{{B}_{1}}\) – проекция \( \displaystyle A{{C}_{1}}\) на плоскость \( \displaystyle A{{A}_{1}}{{B}_{1}}B\).

\( \displaystyle A{{B}_{1}}\bot {{A}_{1}}B\) (так как \( \displaystyle A{{A}_{1}}{{B}_{1}}B\) – квадрат) \( \displaystyle \rightarrow \) по теореме о трех перпендикулярах \( \displaystyle A{{C}_{1}}\bot {{A}_{1}}B\).

Итак, вышло:

\( \displaystyle \left. \begin{array}{l}A{{C}_{1}}\bot BD\\A{{C}_{1}}\bot {{A}_{1}}B\end{array} \right\}\Rightarrow A{{C}_{1}}\bot {{A}_{1}}BD\)

(смотри тему «Перпендикулярность в пространстве», если не совсем хорошо помнишь все теоремы).

Теперь нужно найти \( \displaystyle KM\) — и все!

Вспомним, что \( \displaystyle A{{C}_{1}}^{2}=A{{D}^{2}}+D{{C}^{2}}+C{{C}_{1}}^{2}=1+1+1=3\)\( \displaystyle A{{C}_{1}}=\sqrt{3}\).

Нарисуем теперь плоскость \( \displaystyle A{{A}_{1}}{{C}_{1}}C\) отдельно.

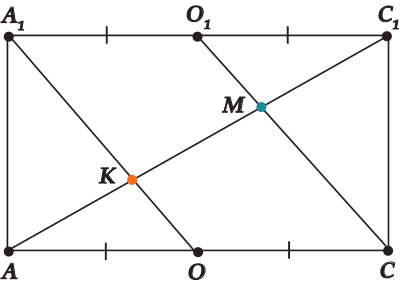
Посмотри внимательно и убедись, что чертеж именно такой! А теперь уже легко:

\( \displaystyle \begin{array}{l}\Delta {{O}_{1}}{{C}_{1}}M\sim \Delta CAM\Rightarrow \frac{{{O}_{1}}{{C}_{1}}}{AC}=\frac{{{C}_{1}}M}{MA}\Rightarrow \frac{1}{2}=\frac{{{C}_{1}}M}{MA}\Rightarrow \\\Rightarrow {{C}_{1}}M=\frac{1}{3}A{{C}_{1}}\end{array}\),

Точно так же \( \displaystyle \Delta AKO\sim \Delta {{C}_{1}}K{{A}_{1}}\Rightarrow AK=\frac{1}{3}A{{C}_{1}}\).

И в итоге: \( \displaystyle KM=A{{C}_{1}}-\frac{1}{3}A{{C}_{1}}-\frac{1}{3}A{{C}_{1}}=-\frac{1}{3}A{{C}_{1}}\).

\( \displaystyle KM=\frac{\sqrt{3}}{3}\).

Вот и нашли.

Не очень–то просто?

Но иногда бывает еще хуже: общего перпендикуляра не видно. Нельзя сказать: вот эта линия перпендикулярна обеим плоскостям. Что же тогда делать?

Для того, чтобы найти расстояние между параллельными плоскостями, часто нужно подобрать удобную точку на одной плоскости и найти расстояние от этой точки до другой плоскости.

Как найти расстояние от точки до плоскости, мы подробно обсуждаем в теме «Расстояние от точки до плоскости».

Здесь же мы рассмотрим один пример, чтобы понять, как же это «подобрать удобную точку» в конкретных задачах.

Решение задачи №2

В правильной шестиугольной пирамиде \( \displaystyle SABCDEF\) точки \( \displaystyle M\) и \( \displaystyle N\) — середины ребер \( \displaystyle SD\) и \( \displaystyle SE\) соответственно.

Найти расстояние между плоскостями \( \displaystyle MNC\) и \( \displaystyle SAB\), если сторона основания пирамиды равна \( \displaystyle 1\), а боковое ребро равно \( \displaystyle 2\).

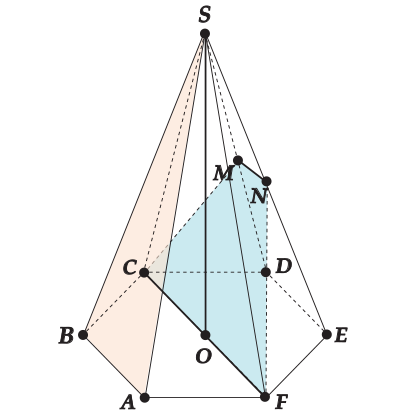
\( \displaystyle CF||MN\Rightarrow \) точка \( \displaystyle F\in CMN\) и \( \displaystyle CMNF\) – трапеция.

Какая же удобная точка?

Вот представь себе – это точка \( \displaystyle O\)!

Почему же?

Ну, во первых она лежит на плоскости \( \displaystyle CMN\) — это уже хорошо. А во-вторых из нее удобно опускать перпендикуляр на плоскость \( \displaystyle SAB\). Давай увидим это:

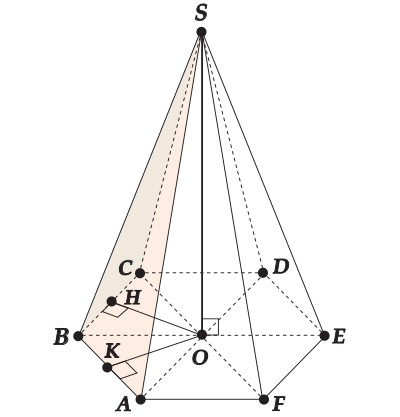
Пусть \( \displaystyle K\) – середина \( \displaystyle AB\).

Тогда \( \displaystyle SK\bot AB\) и \( \displaystyle OK\bot AB\).

Значит \( \displaystyle AB\bot SOK\)

Опустим \( \displaystyle OH\) – высоту в \( \displaystyle \Delta SOK\)

Тогда \( \displaystyle OH\bot SK\) – по построению и \( \displaystyle OH\bot AB\), т.к. \( \displaystyle AB\bot SOK\) \( \displaystyle \rightarrow OH\bot SAB\).

Значит, \( \displaystyle OH\) и есть расстояние между \( \displaystyle SAB\) и \( \displaystyle CMN\).

Осталось это \( \displaystyle OH\) найти.

\( \displaystyle OA=OB=AB=1\Rightarrow OK=1\cdot \sin 60{}^\circ =\frac{\sqrt{3}}{2}\)\( \displaystyle S{{O}^{2}}+O{{E}^{2}}=S{{E}^{2}}\left( \Delta SOE \right)\)

\( \displaystyle S{{O}^{2}}+1=4\Rightarrow S{{O}^{2}}=3\); \( \displaystyle SO=\sqrt{3}\).

\( \displaystyle S{{O}^{2}}+O{{K}^{2}}=S{{K}^{2}}\left( \Delta SOK \right)\Rightarrow \)

\( \displaystyle \Rightarrow 3+\frac{3}{4}=S{{K}^{2}}\); \( \displaystyle SK=\frac{\sqrt{15}}{2}\)

\( \displaystyle OH=\frac{SO\cdot OK}{SK}\) (высота прямоугольного треугольника)

\( \displaystyle OH=\frac{\sqrt{3}\cdot \frac{\sqrt{3}}{2}}{\frac{\sqrt{15}}{2}}=\sqrt{\frac{3}{5}}\)

Ответ: \( \displaystyle \sqrt{\frac{3}{5}}\)