Расстояние от точки до плоскости
Привет!
Стереометрия выглядит жутко… Вернее, сама-то стереометрия красивая!
Знаю, что, когда на уроках скучно, все мы любим порисовать на полях кубы и объемные рисунки 🙂
А вот задачи по стереометрии жутковатые. Однако, если в них хорошо разобраться, все будет легко!
Давай начнем с базы – с расстояния от точки до плоскости.
Поехали!
Расстояние от точки до плоскости — коротко о главном
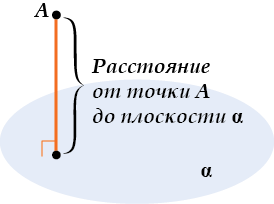
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Существует два способа найти расстояние от точки до плоскости:
- алгебраический;
- геометрический.
Плюсы и минусы обоих способов:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство. |
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно:
- Ввести систему координат;
- Найти координаты точки и уравнение плоскости;
- Применить формулу расстояния от точки до плоскости (Формулу Герона).
\( \displaystyle \rho \)— искомое расстояние
\( \displaystyle \left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)\) — координаты точки \( \displaystyle C\)
\( \displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}}D\) — коэффициенты в уравнении плоскости.
При геометрическом способе нужно:
- Построить перпендикуляр от точки до плоскости;
- Найти точку пересечения перпендикуляра с плоскостью;
- Выполнить необходимое дополнительное построение;
- Определяется расстояние от точки до точки, используя необходимые геометрические теоремы (по ситуации).
А теперь подробнее…
Расстояние от точки до плоскости
Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.
Способы нахождения расстояния от точки до плоскости
Существует, по крайней мере, два способа найти расстояние от точки до плоскости: геометрический и алгебраический.
При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой –то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.
После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).
При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.
Кажется с первого взгляда, что алгебраический способ легче, но это… далеко не всегда так. Проблемы обычно возникают как раз с нахождением координат точки и управления плоскости, особенно если система координат была введена не самым удобным способом. Для удобства приведём плюсы и минусы обоих способов в табличке:
| + | — | |
| АЛГ | Не нужно думать, можно просто применить несколько формул и стандартную процедуру. | Формулы громоздкие, их сложно запомнить, легко допустить ошибку. Особенно если система координат введена неудачно. |
| ГЕО | Не нужно запоминать длинных формул, вычисления обычно не длинные, арифметической ошибке трудно вкрасться. | Нужно уметь применять стереометрические теоремы и понимать, что такое доказательство |
Сейчас мы разберём один достаточно хитрый пример, двумя способами.
Задача: в кубе \( \text{ABCD}~{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) с ребром \( 2\) точки \( \displaystyle M\) — середина ребра \( {{A}_{1}}{{D}_{1}}\). Найти расстояние от точки \( \displaystyle C\) до плоскости \( \displaystyle A{{B}_{1}}M\).

Геометрический способ
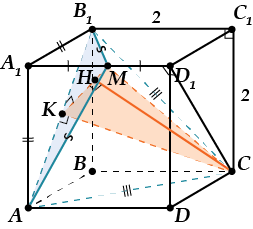
Куда же опускается перпендикуляр из точки \( \displaystyle C\) на плоскость \( \displaystyle A{{B}_{1}}M\)?
Смотрим на \( \displaystyle \Delta A{{B}_{1}}M\) – оказывается, он равнобедренный – \( \displaystyle {{B}_{1}}M=AM\)!
Проведём \( \displaystyle CA\) и \( \displaystyle C{{B}_{1}}\). Зачем? А они тоже равны \( \displaystyle CA\) и \( \displaystyle C{{B}_{1}}\).
Отметим точку \( \displaystyle K\) — середину \( \displaystyle A{{B}_{1}}\) — и проведём \( \displaystyle MK\) и \( \displaystyle CK\). Треугольники \( \displaystyle A{{B}_{1}}M\) и \( \displaystyle A{{B}_{1}}C\) — равнобедренные, поэтому \( \displaystyle MK\bot A{{B}_{1}}\) и \( \displaystyle CK\bot A{{B}_{1}}\).
И вот теперь! Стереометрическая теорема идёт в ход: признак перпендикулярности прямой и плоскости.
\( \displaystyle \left\{ \begin{array}{l}A{{B}_{1}}\bot MK\\A{{B}_{1}}\bot CK\end{array} \right.\Rightarrow A{{B}_{1}}\bot CMK\).
Остался один шаг: проведём \( \displaystyle CH\bot MK\) (в плоскости \( \displaystyle CMK\), естественно).
Что же можно сказать о \( \displaystyle CH\)?
\( \displaystyle CH\bot MK\) по построению
\( \displaystyle CH\bot A{{B}_{1}}\) – так как \( \displaystyle A{{B}_{1}}\bot CMK\) и значит, \( \displaystyle A{{B}_{1}}\) перпендикулярна всякой прямой в плоскости \( \displaystyle CMK\), в частности и \( \displaystyle CH\).
Итак,
\( \displaystyle \left\{ \begin{array}{l}CH\bot MK\\CH\bot A{{B}_{1}}\end{array} \right.\Rightarrow CH\bot A{{B}_{1}}M\) – Ура!
Искомый перпендикуляр из точки \( \displaystyle C\) на плоскость \( \displaystyle A{{B}_{1}}M\) — это высота в \( \displaystyle \Delta CMK\). Осталось найти эту высоту.
\( \displaystyle C{{D}_{1}}=\sqrt{{{2}^{2}}+{{2}^{2}}}=2\sqrt{2}\) (из \( \displaystyle C{{C}_{1}}{{D}_{1}}\)); \( \displaystyle M{{D}_{1}}=1\) (по условию)
\( \displaystyle CM=\sqrt{CD_{1}^{2}+{{D}_{1}}{{M}^{2}}}=\sqrt{8+1}=3\) (из \( \displaystyle \Delta C{{D}_{1}}M\))
Ищем \( \displaystyle KM\):
\( \displaystyle KM=\sqrt{{{B}_{1}}{{M}^{2}}+{{B}_{1}}{{K}^{2}}}=\sqrt{5-2}=\sqrt{3}\ (\Delta {{B}_{1}}KM)\)
Ищем \( \displaystyle CK\):
\( \displaystyle CK=\sqrt{CB_{1}^{2}+{{B}_{1}}{{K}^{2}}}=\sqrt{8-2}=\sqrt{6}\)
Теперь площадь \( \displaystyle \Delta KCM\) по формуле Герона:
Алгебраический способ
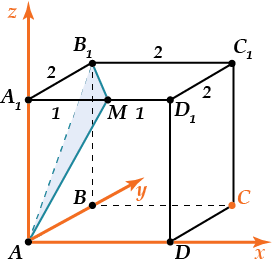
Введём в систему координат с центром в точке \( \displaystyle A\) и осями вдоль рёбер \( \displaystyle A{{D}_{1}}A{{B}_{1}}A{{A}_{1}}\).
Формула для вычисления расстояния от точки до плоскости:
\( \displaystyle \rho =\frac{Ax_0+By_0+Cz_0+D}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}}\)
Найдём всё это от простого к сложному.
Координаты точки \( \displaystyle C\):
\( \displaystyle {{x}_{0}}=2;\ {{y}_{0}}=2;\ {{z}_{0}}=0\).
Чтобы найти уравнение плоскости, сперва найдём три точки, через которые она проходит:
\( \displaystyle A(0;0;0);{{B}_{1}}\left( 0;2;2 \right);M\left( 1;0;2 \right)\).
Подставляем в уравнение плоскости:
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте! Почему не открываются учебники? Регистрацию прошла
Спасибо за ваши старания, помогло!
Отлично, Дмитрий! Успехов на всех экзаменах! )