Равнобедренный треугольник
Среди всех треугольников есть два особенных вида: прямоугольные и равнобедренные.
Чем же эти виды треугольников такие уж особенные?
Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными «действующими лицами» задач ЕГЭ первой части.
А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии.
Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники.
Поехали!
Равнобедренный треугольник — коротко о главном
Определение равнобедренного треугольника
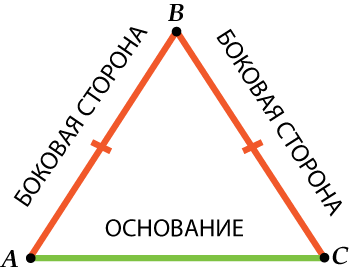
Равнобедренный треугольник – треугольник, у которого есть две равные стороны.
- \( \displaystyle AB=BC\) – боковые стороны
- \( \displaystyle AC\) – основание
Свойства равнобедренного треугольника
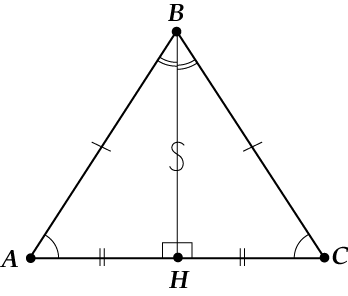
Углы при основании равнобедренного треугольника равны: \( \displaystyle \angle A\ =\angle C\);
Высота, проведённая к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой: \( \displaystyle BH\) — высота, медиана и биссектриса.
Признаки равнобедренного треугольника
Если в некотором треугольнике два угла равны, то он – равнобедренный;
Если в некотором треугольнике совпадают высота и биссектриса или высота и медиана или медиана и биссектриса, проведённые к одной стороне, то такой треугольник – равнобедренный.
Определение равнобедренного треугольника
Треугольник называется равнобедренным, если у него есть две равные стороны.
Посмотри как это выглядит:
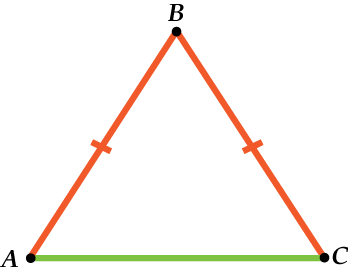
Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон.
Две равные стороны называются боковыми сторонами, а третья сторона – основанием.
И снова внимание на картинку:

Может быть, конечно, и так:
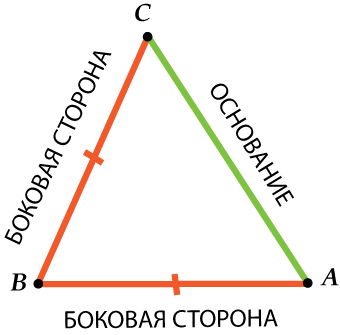
Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник?
Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
Высота равнобедренного треугольника
Высота — это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне.
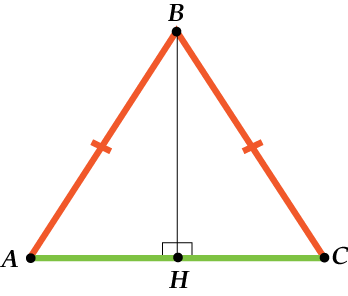
Итак, провели высоту. Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Смотри:
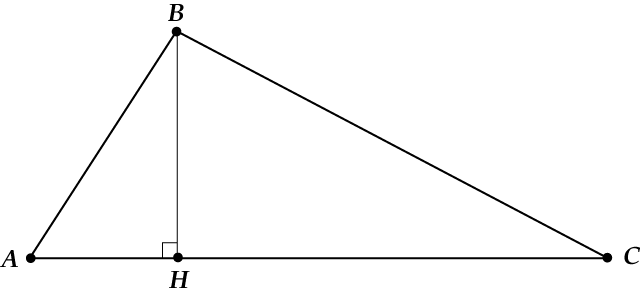
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
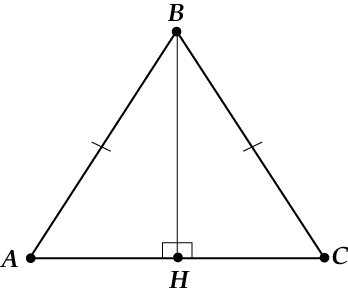
Видишь, два прямоугольных треугольника (Δ???????????? и Δ????????????) – одинаковые!
Или, как математики любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём?
Доказательство равенства треугольников
Посмотри внимательно, у нас есть:
- \( \displaystyle \underbrace{AB}_{гипотенуза \ в\ \Delta ABH}=\underbrace{BC}_{гипотенуза\ в\ \Delta СBH}\)
- \( \displaystyle BH\text{ }=\text{ }BH\) (ещё говорят, \( \displaystyle BH\)— общая)
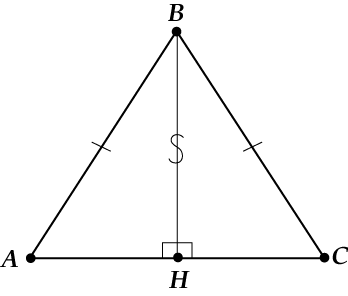
И, значит, \( \displaystyle AH\text{ }=\text{ }CH\)!
Почему?
Да мы просто найдём и \( \displaystyle AH\), и \( \displaystyle CH\) из теоремы Пифагора (помня ещё при этом, что \( \displaystyle AB=BC\))
\( \displaystyle AH=\sqrt{A{{B}^{2}}-B{{H}^{2}}}\)
\( \displaystyle CH=\sqrt{B{{C}^{2}}-B{{H}^{2}}}\)
Удостоверились? Ну вот, теперь у нас
\( \displaystyle \begin{array}{l}AB=BC\\BH=BH\\AH=CH\end{array}\)
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
Отметим на картинке все одинаковые элементы (углы и стороны).
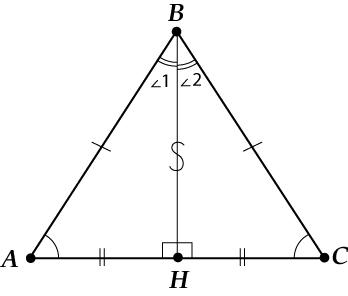
Видишь, как интересно? Получилось, что:
- В равнобедренном треугольнике углы при основании равны: \( \displaystyle \angle A=\angle C\);
- Высота, проведенная к основанию \( \displaystyle (ВH)\), совпадает с медианой и биссектрисой
- \( \displaystyle AH=CH\)
- \( \displaystyle \angle 1=\angle 2\).
Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – делит угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник.
Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?
То есть, как говорят математики, каковы признаки равнобедренного треугольника?
Признаки равнобедренного треугольника
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
Если в каком-то треугольнике есть два равных угла, то такой треугольник –равнобедренный (ну и естественно, углы эти окажутся при основании).
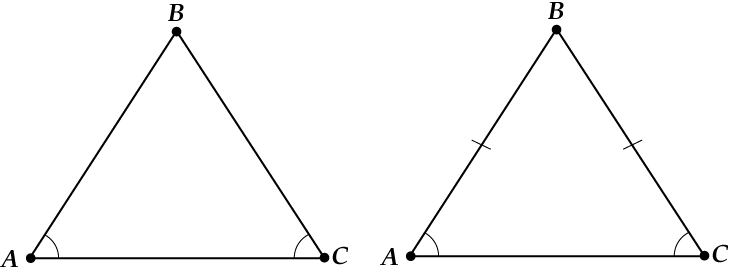
Если в каком-то треугольнике высота и медиана, или высота и биссектриса, или биссектриса и медиана, проведённые к какой-то стороне, совпадут, то такой треугольник – равнобедренный, а сторона эта – основание.
Ну вот смотри:
Если совпадают высота и медиана, то:
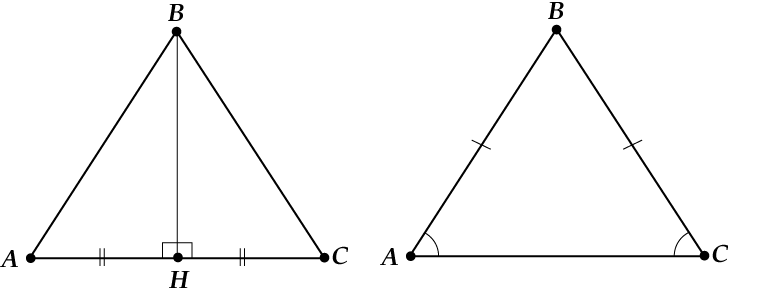
Если совпадают высота и биссектриса, то:
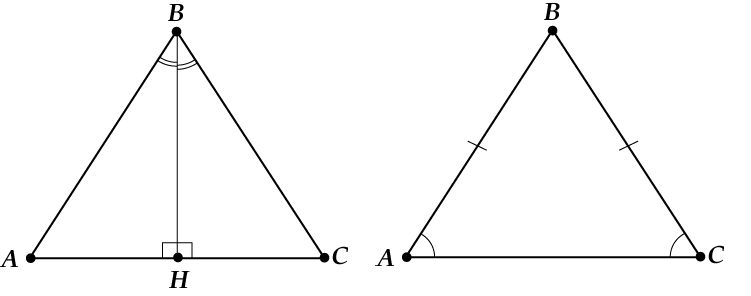
Если совпадают биссектриса и медиана, то:
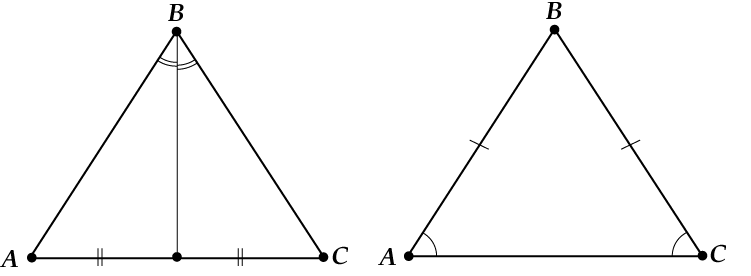
Ну вот, не забывай и пользуйся:
Как пользоваться признаками равнобедренного треугольника при решении задач
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… 🙂 );
- Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
- Если оказалось, что высота разделила угол полам – тоже равнобедренный;
- Если биссектриса разделила сторону пополам или медиана разделила угол, то это тоже бывает только в равнобедренном треугольнике.
Давай посмотрим, как это выглядит в задачах.
2 задачи на равнобедренный треугольник
Задача 1 (самая простая)
В треугольнике \( \displaystyle ABC\) стороны \( \displaystyle AB\) и \( \displaystyle AC\) равны, а \( \displaystyle \angle BAC=70{}^\circ \).
Найти \( \displaystyle \angle ABC\).
Решение
Сначала рисунок:
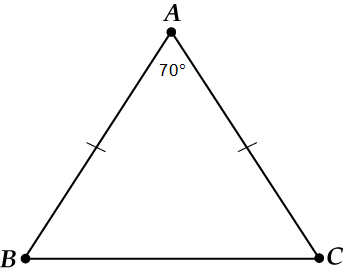
Что здесь основание? Конечно, \( \displaystyle BC\).
Вспоминаем, что если \( \displaystyle AB=AC\), то и \( \displaystyle \angle B=\angle C\).
Обновлённый рисунок:
Задача 2
(Тоже не очень хитрая, но нужно повторить тему «Прямоугольный треугольник»)
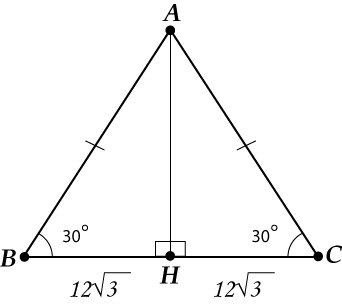
В треугольнике \( \displaystyle ABC\) \( \displaystyle \angle B=\angle C=30{}^\circ \), \( \displaystyle BC=24\sqrt{3}\).
Найти \( \displaystyle AB\).
Решаем:
Смотрим внимательно и соображаем, что раз \( \displaystyle \angle B=\angle C\), то \( \displaystyle AB=AC\).
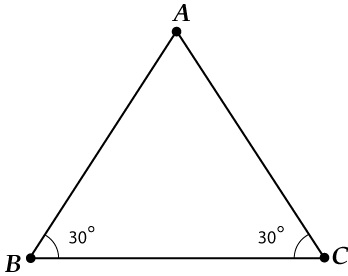
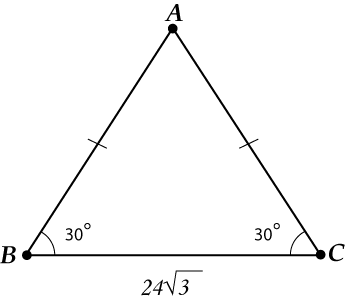
Треугольник-то равнобедренный! Проводим высоту (это и есть фокус, с помощью которого сейчас все решится).
Вспоминаем, что высота = медиана, то есть
\( BH=HC=12\sqrt{3}\).
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Это не просто вебинары, «бла-бла-бла» о теории математики. Это разбор задач в режиме реального времени.
Вы точно научитесь решать любые задачи на эти темы, если их прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.
Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но в этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
На этом уроке мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Также мы научимся решать и «обычные» треугольники. Убедимся в утверждении из прошлого урока — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Что означает обозначение «s» в треугольнике ∆ABC в контексте высоты BH, медианы или биссектрисы?
Это не буква S, это волнистая линия, которой обчно обозначают сторону, если она общая для двух треугольников.
!! ????
Супер коммент! 🙂
Некоторые комментарии прошлых лет к этой статье:
никита
26 сентября 2018
вау помогло все так кратко и понятно
Дмитрий
18 декабря 2019
Очень помогает