Равносторонний треугольник
И вот мы снова изучаем треугольники. Это всё больше похоже на заговор…
Не волнуйся: после прочтения этой статьи тайн не останется, ведь ты будешь знать всё о равностороннем треугольнике!
Тема простая, но очень важная!
Поехали!
Равносторонний треугольник — коротко о главном
Равносторонний треугольник —треугольник, у которого все стороны равны. \(AB=BC=AC=a\)
В равностороннем треугольнике все углы равны между собой и равны \({{60}^{o }}\).
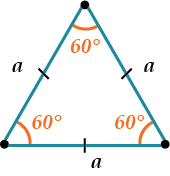
В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой, которые проведены из той же вершины;
Точки пересечения высот, биссектрис, медиан и серединных перпендикуляров равностороннего треугольника совпадают.
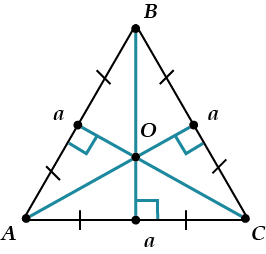
Центры вписанной и описанной окружностей равностороннего треугольника совпадают: точка \(O\);
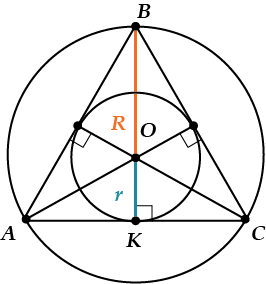
В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны \(a\):
- Высота=медиана=биссектриса: \(h=\frac{a\sqrt{3}}{2}\);
- Радиус описанной окружности: \(R=\frac{a\sqrt{3}}{3}\);
- Радиус вписанной окружности: \(r=\frac{a\sqrt{3}}{6}\);
- Площадь: \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\);
- Периметр: \(P=3a\);
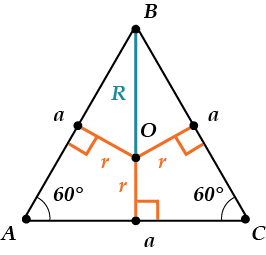
Определение равностороннего треугольника
Равносторонний треугольник —треугольник, у которого все стороны равны.

Какие же особенные свойства присущи равностороннему треугольнику?
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны \({{60}^{o }}\)
Естественно, не правда ли? Три одинаковых угла, в сумме \({{180}^{o }}\), значит, каждый по \({{60}^{o }}\)
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не \(12\) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. \(R=2\cdot r\)
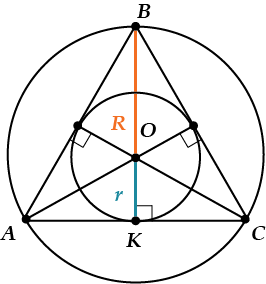
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка\( O\) – центр треугольника.
Значит, \(OB\) – радиус описанной окружности (обозначили его \(R\)), а \(OK\) – радиус вписанной окружности (обозначим \(r\)).
Но ведь точка \(O\) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Поэтому \(OB=2\cdot OK\), то есть \(R=2\cdot r\).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.
Высота равностороннего треугольника
\(h=\frac{a\sqrt{3}}{2}\)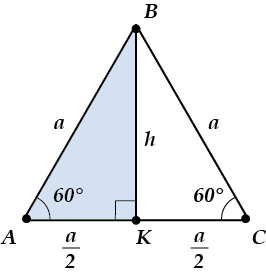
Почему?
Рассмотрим \(\Delta ABK\) – он прямоугольный.
\(\angle A={{60}^{o}}\Rightarrow h=a\cdot \sin {{60}^{o}}=\frac{a\sqrt{3}}{2}\)Радиус описанной окружности равностороннего треугольника
\(R=\frac{a\sqrt{3}}{3}\)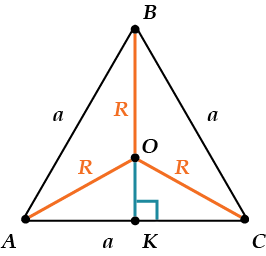
А это почему?
Радиус вписанной окружности равностороннего треугольника
\(r=\frac{a\sqrt{3}}{6}\)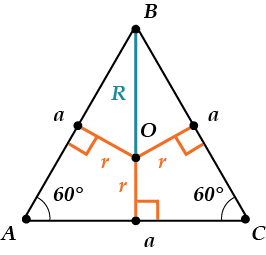
Это уже теперь должно быть совсем ясно:
Бонус 1. Статьи о других треугольниках
Подробная информация о других треугольниках в следующих статьях:
А в нашем учебнике по подготовке к ЕГЭ по математике вы найдете подробную информацию о других разделах математики:
Бонус 2: Вебинары о треугольниках, чтобы набить руку в решении задач
А в этих видео из нашего курса подготовки к ЕГЭ по математике вы можете потренироваться, решая задачи вместе с нашим репетитором Алексеем Шевчуком.
Это не просто вебинары, «бла-бла-бла» о теории математики. Это разбор задач в режиме реального времени.
Вы точно научитесь решать любые задачи на эти темы, если их прослушаете.
Хотите получить максимум от этих вебинаров? Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
ЕГЭ 6. Прямоугольный треугольник: свойства, теорема Пифагора, тригонометрия
Подавляющее большинство задач в планиметрии решается через прямоугольные треугольники.
Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.
Но в этом видео мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.
На этом уроке мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.
ЕГЭ 6. Равнобедренный треугольник, произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Также мы научимся решать и «обычные» треугольники. Убедимся в утверждении из прошлого урока — очень часто решение задач сводится к нескольким прямоугольным треугольникам.
ЕГЭ 16. Подобие треугольников. Задачи на доказательство
Итак, задача 16 профильного ЕГЭ. Подобие треугольников. Это одна из самых сложных задачи в профильном ЕГЭ.
Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Gabit
18 сентября 2019
Спасибо большое, хоть дочка и учится в школе с другим языком обучения, символы в математике едины и Ваша статья ей помогла.