Целые числа (натуральные и отрицательные числа, НОК и НОД)
Чтобы намного упростить себе жизнь когда надо что-то вычислить, чтобы выиграть драгоценное время на ОГЭ или ЕГЭ, чтобы сделать меньше глупых ошибок, – читай эту статью!
Вот чему ты научишься:
- как быстрее, легче и точнее считать, используя группировку чисел при сложении и вычитании,
- как без ошибок, быстро умножать и делить, используя правила умножения и признаки делимости,
- как значительно ускорить расчеты с помощью наименьшего общего кратного (НОК) и наибольшего общего делителя (НОД).
Поехали!
Целые числа — коротко о главном
Множество целых чисел состоит из 3 частей:
- натуральные числа;
- числа, противоположные натуральным;
- ноль – «0»
Множество целых чисел обозначается буквой Z.
Натуральные числа
Натуральные числа – это числа, которые мы употребляем для счета предметов.
1, 2, 3, 4…????
Множество натуральных чисел обозначается буквой N.
В операциях с целыми числами понадобится умение находить НОД и НОК.
Наибольший общий делитель (НОД)
Чтобы найти НОД, необходимо:
- Разложить числа на простые множители (на такие числа, которые нельзя разделить ни на что больше, кроме самого себя или на 1, например, 3, 7, 11, 13 и т.д.).
- Выписать множители, которые входят в состав обоих чисел.
- Перемножить их.
Наименьшее общее кратное (НОК)
Чтобы найти НОК, необходимо:
- Разложить числа на простые множители (это ты уже отлично умеешь делать).
- Выписать множители входящие в разложение одного из чисел (лучше брать самую длинную цепочку).
- Добавить к ним недостающие множители из разложений остальных чисел.
- Найти произведение получившихся множителей.
Отрицательные числа
Числа, противоположные натуральным, то есть:
−1; −2; −3; −4 и т.д.
Ноль
Не дели на ноль! ????
Натуральные числа
Множество целых чисел состоит из 3 частей:
- натуральные числа (рассмотрим их подробнее чуть ниже);
- числа, противоположные натуральным (все станет на свои места, как только ты узнаешь, что такое натуральные числа);
- ноль – «0« (куда уж без него?)
Множество целых чисел обозначается буквой Z.
«Бог создал натуральные числа, всё остальное – дело рук человеческих» (c) Немецкий математик Кронекер.
Натуральные числа – это числа, которые мы употребляем для счета предметов, и именно на этом основывается их история возникновения – необходимости считать стрелы, шкуры и т.д.
1, 2, 3, 4… n
Множество натуральных чисел обозначается буквой N.
Соответственно, в это определение не входит 0 (не можешь же ты посчитать то, чего нет?) и тем более не входят отрицательные значения (разве бывает -1 яблоко?).
Кроме этого, не входят и все дробные числа (мы также не можем сказать « у меня есть 1,5 ноутбука», или «я продал 2,5 машины»)
Любое натуральное число можно записать с помощью 10 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Таким образом, 14 – это не цифра. Это число. Из каких цифр оно состоит? Правильно, из цифр 1 и 4.
Натуральные числа можно складывать, вычитать, умножать и делить.
Сложение. Группировка при сложении чисел
Что интересного ты можешь сказать про эту процедуру?
Конечно, ты сейчас ответишь «от перестановки слагаемых значение суммы не меняется».
Казалось бы, примитивное, знакомое с первого класса правило, однако, при решении больших примеров оно моментально забывается!
Не забывай про него — используй группировку, чтобы облегчить себе процесс подсчета и снизить вероятность ошибок, ведь на ЕГЭ калькулятора у тебя не будет.
Смотри сам, какое выражение легче сложить?
- 4 + 5 + 3 + 6
- 4 + 6 + 5 + 3
Конечно же второе! Хотя результат один и тот же. Но! считая вторым способом у тебя меньше шансов ошибиться и ты все сделаешь быстрее!
Итак, ты в уме считаешь вот так:
4 + 5 + 3 + 6 = 4 + 6 + 5 + 3 = 10 + 5 + 3 = 18
Вычитание. Группировка при вычитании чисел
При вычитании мы также можем группировать вычитаемые числа, например:
32 — 5 — 2 — 6 = (32 — 2) — 5 — 6 = 30 — 5 — 6 = 19
А что, если вычитание чередуется в примере со сложением? Так же можно группировать, ответишь ты, и это правильно. Только прошу, не забывай о знаках перед числами, например: 32 — 5 — 2 — 6 = (32 — 2) — (6 + 5) = 30 — 11 = 19
Помни: неправильно проставленные знаки приведут к ошибочному результату.
Очевидно, что от перемены мест множителей значение произведения также не изменится:
2⋅4⋅6⋅5=(2⋅5)⋅(4⋅6)=10⋅24=240
Я не буду говорить тебе «используй это при решении примеров» (ты и сам понял намек, правда?), а лучше расскажу, как быстро умножать некоторые числа в уме.
Умножение. Как быстро умножать в уме
Итак, внимательно смотри таблицу:
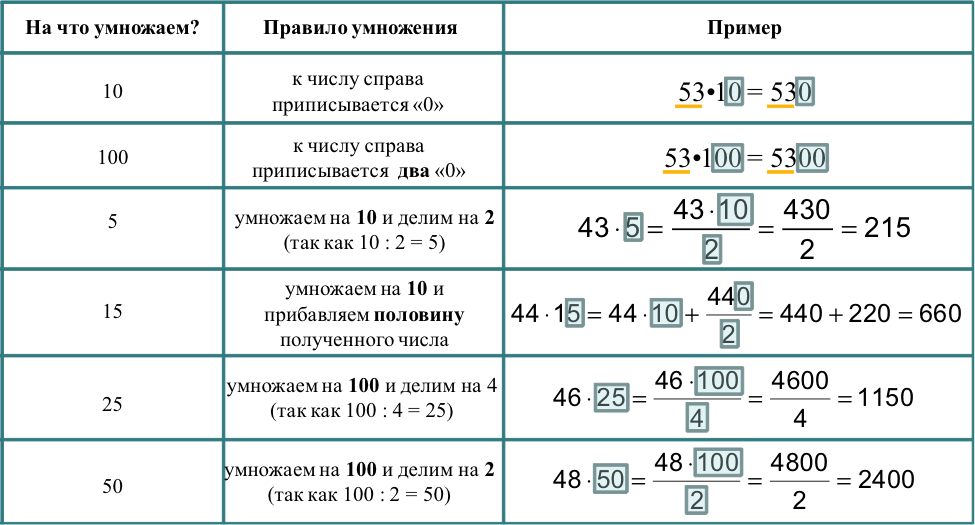
И еще немного об умножении. Конечно, ты помнишь два особых случая…
Догадываешься, о чем я?
Вот об этом:
а * 0 = 0
a * 1 = a
Ну что здесь можно сказать интересного?
Число может делиться на другое нацело (то есть, без остатка) и с остатком, который всегда меньше делителя, что вполне логично.
Особые случаи, если при делении у нас есть 0.
Чему будет равен пример, если 0 является делителем и чему равен пример, если он делимое?
Правильно:
a:0 – нельзя!
0:a=0
Ах да, еще рассмотрим признаки делимости.
Всего существует 7 правил по признакам делимости, из которых первые 3 ты точно уже знаешь!
А вот остальные совсем не сложно запомнить.
Признаки делимости чисел
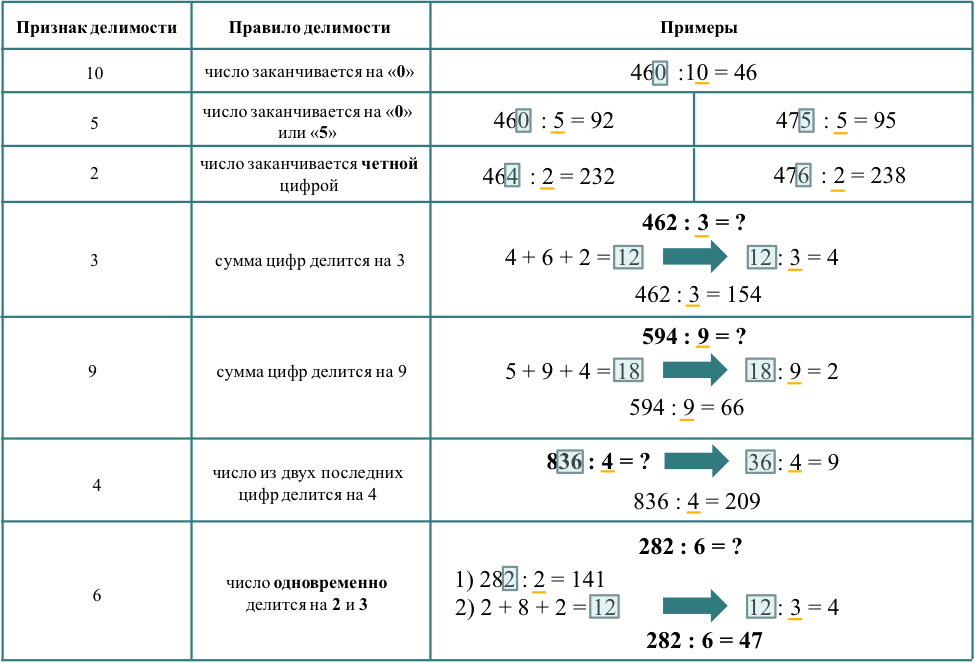
Первые три правила ты, конечно же, знаешь.
Четвертое и пятое легко запомнить – при делении на 3 и 9 мы смотрим, делится ли на это сумма цифр, составляющих число.
При делении на 4 мы обращаем внимание на две последние цифры числа — делится ли число, которое они составляют на 4?
При делении на 6 число должно одновременно делиться на 2 и на 3. Вот и вся премудрость.
Ты сейчас думаешь: «зачем мне все это»?
Во-первых, ЕГЭ проходит без калькулятора и данные правила помогут тебе сориентироваться в примерах.
А во-вторых, ты же слышал задачи про НОД и НОК? Знакомая аббревиатура? Начнем вспоминать и разбираться.
Наибольший общий делитель (НОД)
Наибольший общий делитель (НОД) — нужен для сокращения дробей и быстрых вычислений.
Допустим, у тебя есть два числа: 12 и 8.
На какое наибольшее число делятся оба этих числа? Ты, не задумываясь, ответишь 4, потому что знаешь, что:
12 = 4 * 3 = 2 * 2 * 3
8 = 4 * 2 = 2 * 2 * 2
Какие цифры в разложении общие?
Правильно, 2 * 2 = 4. Вот и твой ответ был 4.
Держа в голове этот простой пример, ты не забудешь алгоритм, как находить НОД.
Попробуй «выстроить» его у себя в голове. Получилось?
Чтобы найти НОД необходимо:
- Разложить числа на простые множители (на такие числа, которые нельзя разделить ни на что больше, кроме самого себя или на 1, например, 3, 7, 11, 13 и т.д.).
- Выписать множители, которые входят в состав обоих чисел.
- Перемножить их.
Понимаешь, зачем нам нужны были признаки делимости? Чтобы ты посмотрел на число и мог начать делить без остатка.
Найдем НОД числа 290
Глядя на него, ты сразу можешь сказать, что оно делится на 10, запишем:
290 = 29 * 10
29 больше разделить ни на что нельзя, а вот 10 можно – 5 и 2, получаем:
290 = 29 * 5 * 2
Найдем НОД числа 485.
По признакам делимости оно должно без остатка делиться на 5, так как на 5 заканчивается. Делим:
485 = 5 * 97
Проанализируем изначальное число.
На 2 оно делиться не может (последняя цифра – нечетная),
85 – не делится на 4, значит число тоже не делится на 4,
На 3 и на 9 также не делится (сумма цифр, входящих в число, не делится на 3 и на 9)
На 6 тоже не делится, так как не делится на 2 и 3,
На 8 тоже не делится, так как не делится на 2 и 4.
97 нельзя разделить на 7 нацело,
Значит, число 485 можно разложить только на 5 и 97.
А теперь найдем НОД этих чисел (290 и 485).
Какое это число?
Правильно, 5.
Совет: глядя на числа можно иногда сразу найти хотя бы один общий делитель. Раздели сначала на него, а потом уже раскладывай дальше. При этом, необязательно общий делитель раскладывать на его составляющие – все равно потом ты будешь их снова перемножать.
Задача №1. Найти НОД чисел 6240 и 6800
1) Делю сразу на 10, так как оба числа 100% делятся на 10:
6240 = 10 * 624
6800 = 10 * 680
2) Разделю на 4 оставшиеся большие числа (624 и 680), так как 24 и 80 без остатка делятся на 4 (при этом, 10раскладывать не буду – он и так общий делитель):
6240=10⋅4⋅156
6800=10⋅4⋅170
3) Оставлю 4 и 10 в покое и начну рассматривать числа 156 и 170. Оба числа точно делятся на 2 (заканчиваются на четные цифры (0 в таком случае представляем как 10, а 10 можно разделить на 2)):
6240=10⋅4⋅2⋅78
6800=10⋅4⋅2⋅85
4) Работаем с числами 78 и 85. Есть ли у них общие делители? Так легко, как в предыдущих действиях, и не скажешь, поэтому дальше просто разложим их на простые множители:
6240=10⋅4⋅2⋅2⋅39
6800=10⋅4⋅2⋅5⋅17
5) Как мы видим, мы были правы: у 78 и 85 общих делителей нет, и теперь нам нужно перемножить 10⋅4⋅2=80.
НОД (6240; 6800)=80
Задача №2. Найти НОД чисел 345 и 324
Здесь не могу быстро найти хоть один общий делитель, так что просто раскладываю на простые множители (как можно меньше):
345=5⋅69=5⋅3⋅23
324=2⋅162=2⋅2⋅81=2⋅2⋅9⋅9=2⋅2⋅3⋅3⋅3⋅3
Точно, НОД (345; 324)=3, а я изначально не проверила признак делимости на 3, и, возможно, не пришлось бы делать столько действий.
Но ты-то проверил, верно?
Молодец!
Как видишь, это совсем несложно.
Наименьшее общее кратное (НОК) — экономит время, помогает решить задачи нестандартно
Допустим, у тебя есть два числа – 8 и 16. Какое существует самое маленькое число, которое делится 8 и 16 без остатка(то есть нацело)? Сложно представить? Вот тебе визуальная подсказка:
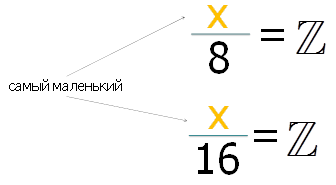
Ты же помнишь, что обозначается буквой ℤ? Правильно, как раз целые числа. Так какое наименьшее число подходит на место х? ????=16:
16:8=2
16:16=1
В данном случае НОК(8;16)=16.
Из этого простого примера вытекает несколько правил.
Наименьшее общее кратное (НОК)
Правила быстрого нахождения НОК.
Правило 1
Если одно из двух натуральных чисел делится на другое число, то большее из этих двух чисел является их наименьшим общим кратным.
Найди НОК у следующих чисел:
- 1НОК (7;21)
- 2НОК (6;12)
- 3НОК (5;15)
- 4НОК (3;33)
Конечно, ты без труда справился с этой задачей и у тебя получились ответы – 21,12, 15 и 33.
Заметь, в правиле мы говорим о ДВУХ числах, если чисел будет больше, то правило не работает.
Например, НОК (7;14;21) не равно 21, так как 21не делится без остатка на 14.
Правило 2
Если два (или более двух) числа являются взаимно простыми, то наименьшее общее кратное равно их произведению.
Найди НОК у следующих чисел:
- 1НОК (1;3;7)
- 2НОК (3;7;11)
- 3НОК (2;3;7)
- 4НОК (3;5;2)
Посчитал? Вот ответы – 21, 231, 42; 30.
Как ты понимаешь, не всегда можно так легко взять и подобрать этот самый х, поэтому для чуть более сложных чисел существует следующий алгоритм:
- Разложить числа на простые множители (это ты уже отлично умеешь делать).
- Выписать множители входящие в разложение одного из чисел (лучше брать самую длинную цепочку).
- Добавить к ним недостающие множители из разложений остальных чисел.
- Найти произведение получившихся множителей.
Найдем наименьшее общее кратное – НОК (345; 234)
Раскладываем каждое число:
345=5⋅69=5⋅3⋅23
234=3⋅2⋅39=3⋅2⋅3⋅13
Почему я сразу написал 3⋅2?
Вспомни признаки делимости на 6: делится на 2 (последняя цифра – четная) и сумма цифр делится на 3 (2+3+4=9).
Соответственно, можем сразу разделить 234 на 6, записав ее как 3⋅2.
Теперь выписываем в строчку наиболее длинное разложение – второе:
3⋅2⋅3⋅13
Добавим к нему числа из первого разложения, которых нет в том, что мы выписали:
3⋅2⋅3⋅13⋅5⋅23
Заметь: мы выписали все кроме 3, так как она у нас уже есть.
Теперь нам необходимо все эти числа перемножить!
3⋅2⋅3⋅13⋅5⋅23=18⋅13⋅5⋅23=18⋅65⋅23=26910
НОК(345;234)=26910
Найди наименьшее общее кратное (НОК) (6240;6800) и (345;324)
Какие ответы у тебя получились?
Вот, что вышло у меня:
НОК(6240;6800)=530400
НОК(345;234)=37260
Сколько времени ты потратил на нахождение НОК? Мое время – 2 минуты, правда я знаю одну хитрость, которую предлагаю тебе открыть прямо сейчас!
Если ты очень внимателен, то ты наверное заметил, что по заданным числам мы уже искали НОД и разложение на множители этих чисел ты мог взять из того примера, тем самым упростив себе задачу, но это далеко не все.
Посмотри на картинку, возможно, к тебе придут еще какие-нибудь мысли:
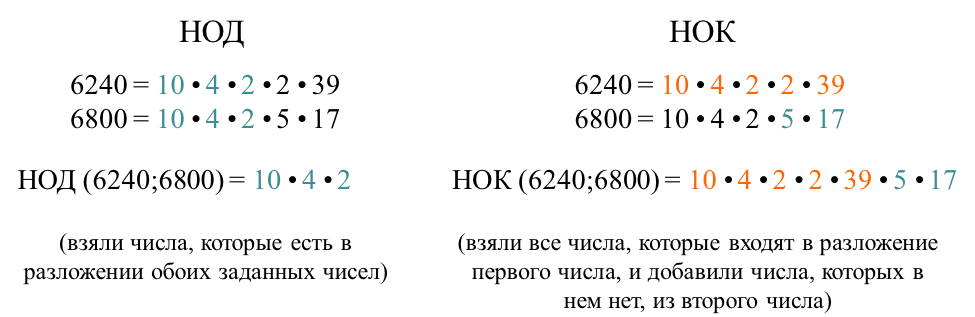
Ну что? Сделаю подсказку: попробуй перемножить НОК и НОД между собой и запиши все множители, которые будут при перемножении. Справился? У тебя должна получиться вот такая цепочка:
10⋅4⋅2⋅10⋅4⋅2⋅2⋅39⋅5⋅17
Присмотрись к ней повнимательней: сравни множители с тем, как раскладываются 6240 и 6800.
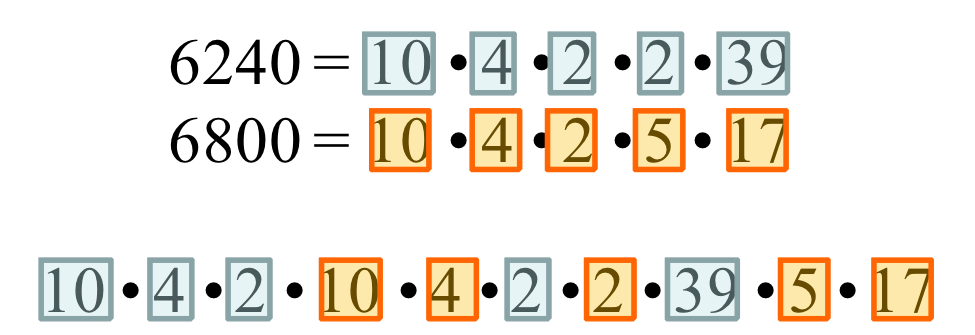
Какой вывод ты можешь сделать из этого? Правильно! Если мы перемножим значения НОК и НОД между собой, то мы получим произведение этих чисел.
Соответственно, имея числа и значение НОД (или НОК), мы можем найти НОК (или НОД) по такой схеме:
1. Находим произведение чисел:
6240⋅6800=42432000
2. Делим получившееся произведение на наш НОД (6240; 6800) = 80:
42432000:80=530400
Вот и все.
Запишем правило в общем виде:
НОК (????;????)⋅ НОД (????;????)=????⋅????
Попробуй найти НОД, если известно, что:
НОК(345; 234)=26910
Справился? НОД(345; 234)=3.
Отрицательные числа – «лжечисла» и их признание человечеством
Как ты уже понял, это числа, противоположные натуральным, то есть:
−1; −2; −3; −4 и т.д.
Отрицательные числа можно складывать, вычитать, умножать и делить – все как в натуральных.
Казалось бы, что в них такого особенного?
А дело в том, что отрицательные числа «отвоевывали» себе законное место в математике аж до XIX века (до этого момента было огромное количество споров, существуют они или нет).
Само отрицательное число возникло из-за такой операции с натуральными числами, как «вычитание».
Действительно, из 3 вычесть 11 – вот и получается отрицательное число. Именно поэтому, множество отрицательных чисел часто называют «расширением множества натуральных чисел».
Отрицательные числа долго не признавались людьми.
Так, Древний Египет, Вавилон и Древняя Греция – светочи своего времени, не признавали отрицательных чисел, а в случае получения отрицательных корней в уравнении (например, как у нас 3−11), корни отвергались как невозможные.
Впервые отрицательные числа получили свое право на существование в Китае, а затем в VII веке в Индии.
Как ты думаешь, с чем связано это признание?
Правильно, отрицательными числами стали обозначать долги (иначе — недостачу).
Считалось, что отрицательные числа – это временное значение, которое в результате изменится на положительное (то есть, деньги кредитору все же вернут). Однако, индийский математик Брахмагупта уже тогда рассматривал отрицательные числа наравне с положительными.
В Европе к полезности отрицательных чисел, а также к тому, что они могут обозначать долги, пришли значительно позже, эдак, на тысячелетие.
Первое упоминание замечено в 1202 году в «Книге абака» Леонарда Пизанского (сразу говорю — к Пизанской башне автор книги отношения никакого не имеет, а вот числа Фибоначчи – это его рук дело (прозвище Леонардо Пизанского — Фибоначчи)).
Далее европейцы пришли к тому, что отрицательные числа могут обозначать не только долги, но и нехватку чего бы то ни было, правда, признавали это не все.
Так, в XVII веке Паскаль считал что 0−4=0.
Как думаешь, чем он это обосновывал?
Верно, «ничто не может быть меньше НИЧЕГО».
Отголоском тех времен остается тот факт, что отрицательное число и операция вычитания обозначается одним и тем же символом – минусом «-». И правда: 6−8. Число «8» положительное, которое вычитается из 6, или отрицательное, которое суммируется к 6?… Что-то из серии «что первое: курица или яйцо?» Вот такая вот, своеобразная эта математическая философия.
Отрицательные числа закрепили свое право на существование с появлением аналитической геометрии, иначе говоря, когда математики ввели такое понятие как числовая ось.
Именно с этого момента наступило равноправие. Однако все равно вопросов было больше чем ответов, например:
пропорция \( \displaystyle \frac{1}{-1}=\frac{-1}{1}\)
Данная пропорция носит название «парадокс Арно». Подумай, что в ней сомнительного?
Давай рассуждать вместе «\( \displaystyle 1\)» больше, чем «\( \displaystyle -1\)» верно? Таким образом, согласно логике, левая часть пропорции должна быть больше, чем правая, но они равны… Вот он и парадокс.
В итоге, математики договорились до того, что Карл Гаусс (да, да, это тот самый, который считал сумму \( \displaystyle 40\) (или \( \displaystyle 100\)) чисел) в 1831 году поставил точку.
Он сказал, что отрицательные числа имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, так как дроби так же не применимы ко многим вещам (не бывает так, что яму роют \( \displaystyle 1,5\) землекопа, нельзя купить \( \displaystyle 4,5\) билета в кино и т.д.).
Успокоились математики только в XIX веке, когда Уильямом Гамильтоном и Германом Грассманом была создана теория отрицательных чисел.
Вот такие они спорные, эти отрицательные числа.
Возникновение «пустоты» или биография нуля
В математике \( \displaystyle 0\) – особенное число.
С первого взгляда, это ничто: прибавить \( \displaystyle 0\), отнять \( \displaystyle 0\) – ничего не изменится, но стоит только приписать его справа к «\( \displaystyle 1\)», и полученное число \( \displaystyle 10\) будет в \( \displaystyle 10\) раз больше изначального.
Умножением на ноль мы все превращаем в ничто, а разделить на «ничто», то есть \( \displaystyle 0\), мы не можем. Одним словом, волшебное число)
История нуля длинная и запутанная.
След нуля найден в сочинениях китайцев во 2 тыс. н.э. и ещё раньше у майя. Первое использование символа нуля, каковым он является в наши дни, было замечено у греческих астрономов.
Существует множество версий, почему было выбрано именно такое обозначение «ничего».
Некоторые историки склоняются к тому, что это омикрон, т.е. первая буква греческого слова ничто – ouden. Согласно другой версии, жизнь символу ноля дало слово «обол» (монета, почти не имеющая ценности).
Ноль (или нуль) как математический символ впервые появляется у индийцев (заметь, там же стали «развиваться» отрицательные числа).
Первые достоверные свидетельства о записи нуля относятся к 876 г., и в них «\( \displaystyle 0\)» – составляющая числа \( \displaystyle 270\).
В Европу ноль также пришел с запозданием — лишь в 1600г., и также как и отрицательные числа, сталкивался с сопротивлением (что поделаешь, такие они, европейцы).
«Нуль часто ненавидели, издавна боялись, а то и запрещали» — пишет американский математик Чарльз Сейф.
Так, турецкий султан Абдул-Хамид II в конце XIXв. приказал своим цензорам вычеркнуть из всех учебников химии формулу воды H2O, принимая букву «О» за нуль и не желая, чтобы его инициалы порочились соседством с презренным нулём».
На просторах интернета можно встретить фразу: «Ноль — самая могущественная сила во Вселенной, он может всё! Ноль создаёт порядок в математике, и он же вносит в неё хаос». Абсолютно верно подмечено:)
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Здравствуйте. Замечательная статья. Спасибо! Единственное, непонятно практическое применение НОКа.
Спасибо, Наталья. Да, наше упущение. Действительно в статье нет примеров применения НОК, но на самом деле все просто. Как обычно, математики — лентяи, поэтому придумывают способы как упростить себе жизнь и сократить вычисления. НОК и НОД необходимы для упрощения работы с целыми числами.
Самый простой пример — сложение и вычитание дробей, то есть необходимость привести дроби к общему знаменателю. Если в знаменателе небольшие простые числа, проблем нет. Например, если нужно из 2/3 вычесть 1/5, мы перемножаем 3 на 5, получаем 15 в общем знаменателе и спокойно решаем пример. 10/15-3/15=7/15
А если, например, нужно из 9/18 вычесть 5/24, то тут уже «не выгодно» просто перемножить 18 и 24, особенно когда этот пример — часть более сложного примера. Во-первых, устно не получится, во-вторых, можно наделать ошибок, в-третьих, времени займет больше. Вот тут и нужно посчитать НОД и взять его за общий знаменатель. Вместо числа 432 вы будете работать с числом 72. В итоге, меньше ошибок и меньше времени.
Ну и при решении 18 задачи на свойства чисел без умения находить НОК и НОД никуда. Вот примеры 18 задачи: https://youclever.org/book/19-ege-math-teoriya-chisel/
Некоторые комментарии прошлых лет к этой статье:
Алексей
26 декабря 2018
замечательный сайт, благодарность создателям
Александр (админ)
26 декабря 2018
Спасибо, Алексей! Очень приятно слышать!
Дмитрий
28 февраля 2019
Просто топ!!!
Александр (админ)
28 февраля 2019
Просто спасибо, Дмитрий!)
Маша
21 апреля 2019
Супер!!! Раньше тема НОК и НОД для меня была какой-то не очень интересной… Да и примеры на эту тему решались как-то долго и в основном неправильно… Теперь — всё понятно , я решаю примеры правильно и с удовольствием! P. S С ВАШИМ УЧЕБНИКОМ МАТЕМАТИКА ДЛЯ МЕНЯ СТАЛА ИНТЕРЕСНОЙ!!! КАК ЭТО КРУТО, ЧТО ВЫ ЕСТЬ!!! (Лучше учебника я реально не видела)
Александр (админ)
21 апреля 2019
Маша, ради таких комментариев я и поддерживаю этот учебник на плаву. Очень приятно! Спасибо и удачи на всех экзаменах жизни! 🙂
Дмитрий
09 июля 2019
Очень крутой сайт! Спасибо автору 🙂
Александр (админ)
09 июля 2019
Спасибо, Дмитрий! Очень приятно, что даже на каникулах кто-то читает наш сайт )
Алина
30 октября 2019
Очень нравится оформление сайта, темы удобно разделены и понятно расписаны. Хочу самостоятельно изучить математику, закрыть «дыры» в знаниях. Надеюсь, этот учебник мне в этом поможет. Огромная вам благодарность, Александр!
Александр (админ)
30 октября 2019
Очень приятно слышать такие слова, Алина. Спасибо большое. Учебник конечно же поможет. Я скоро выложу новые версии обоих моих сайтов, посвященных изучению математики: учебник YouClever и решебник 100gia. Надеюсь будет еще удобнее.