Скрещивающиеся прямые
Как определяется угол между скрещивающимися прямыми?
Ты можешь спросить, а чего тут определять? Угол, он и в Африке (то есть в пространстве) – угол!
И действительно, если прямые лежат в одной плоскости, то угол между ними ищется так же, как и на плоскости:
Наименьший из двух углов, образованных при пересечении.

Но что же делать, если прямые совсем не пересекаются?
Читай эту статью и всё узнаешь!
Скрещивающиеся прямые — коротко о главном
Если прямые лежат в разных плоскостях (т.е. не пересекаются), нужно через произвольную точку на одной прямой (например, прямой \( \displaystyle a\)) провести прямую, параллельную другой прямой (например, прямую \( \displaystyle {a}’||a\)).

Скрещивающиеся прямые — подробнее
Как найти угол, если прямые не пересекаются?
Вот, например: прямые \( \displaystyle a\) и \( \displaystyle b\) скрещиваются. Какой угол между ними?
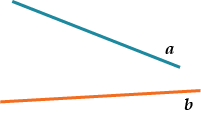
Чтобы это определить, делаем так: через произвольную точку одной прямой (например \( \displaystyle b\)), нужно провести прямую \( \displaystyle {a}’||a\).

И тогда угол между \( \displaystyle a\) и \( \displaystyle b\) будет равен (по определению!) углу между \( \displaystyle {{a}’}\) и \( \displaystyle b\).
Да, но как это применить в задачах? Давай посмотрим.
Решение задач на угол между скрещивающимися прямыми
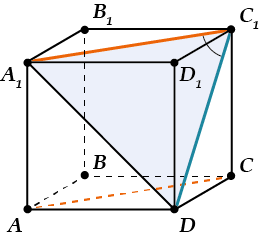
В кубе \( \displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) найти угол между \( \displaystyle AC\) и \( \displaystyle D{{C}_{1}}\).
Решаем:
Прямые \( \displaystyle AC\) и \( \displaystyle D{{C}_{1}}\) не пересекаются, но нужно как-то найти угол между ними.
Пользуемся правилом: через точку \( \displaystyle {{C}_{1}}\) проведем прямую \( \displaystyle {{A}_{1}}{{C}_{1}}\). Она будет параллельна \( \displaystyle AC\).
Значит, угол между \( \displaystyle AC\) и \( \displaystyle D{{C}_{1}}\) равен углу между \( \displaystyle {{A}_{1}}{{C}_{1}}\) и \( \displaystyle D{{C}_{1}}\). Осталось его найти.
Смотри: \( \displaystyle {{A}_{1}}{{C}_{1}}\), \( \displaystyle {{A}_{1}}D\) и \( \displaystyle D{{C}_{1}}\) – диагонали граней куба, поэтому \( \displaystyle {{A}_{1}}{{C}_{1}}={{C}_{1}}D={{A}_{1}}D\), то есть \( \displaystyle \Delta {{A}_{1}}{{C}_{1}}D\) – равносторонний.
Поэтому \( \displaystyle \angle {{A}_{1}}{{C}_{1}}D=60{}^\circ \).
Ответ: \( \displaystyle 60{}^\circ \).
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
Задачи на скрещивающиеся прямые и углы между ними попадаются сплошь и рядом в этом вебинаре.
ЕГЭ 8. Куб. Параллелепипед. Призма – расстояния и углы в пространстве
На этом уроке мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



ОЧЕНЬ КРУТО! ТАК ПОНЯТНО ! СПАСИБООО!
И вам спасибо! 🙂