Вписанный четырехугольник и его свойства
Мы видели, что вокруг всякого треугольника можно описать окружность. Вот так:

Вопрос: а можно ли получить вписанный четырехугольник?
Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?
Сейчас мы это выясним!
Вписанный четырехугольник — коротко о главном
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна \( \displaystyle 180{}^\circ \)
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна \( \displaystyle 180{}^\circ \), то такой четырехугольник вписанный.
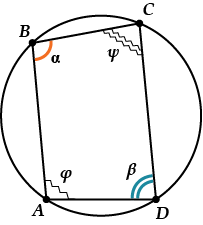
Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна \( \displaystyle 180{}^\circ \).
\( \displaystyle \angle B+\angle D=180{}^\circ \).
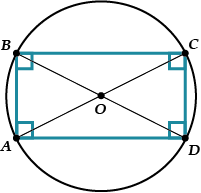
Параллелограмм, вписанный в окружность – непременно прямоугольник, и центр окружности совпадает с точкой пересечения диагоналей.
- Трапеция, вписанная в окружность – равнобокая.
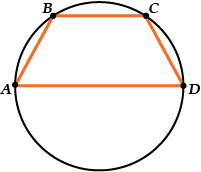
Вписанный четырехугольник — определения и теоремы
Вот оказывается, что это неправда!
НЕ ВСЕГДА четырехугольник можно вписать в окружность.
Есть очень важное условие:
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна \( \displaystyle 180{}^\circ \).
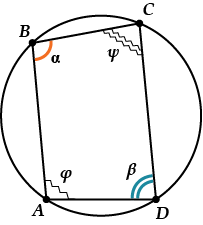
На нашем рисунке: \( \displaystyle \alpha +\beta =180{}^\circ \)
Посмотри, углы \( \displaystyle \alpha \) и \( \displaystyle \beta \) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами \( \displaystyle \varphi \) и \( \displaystyle \psi \)? Они вроде бы тоже противоположные?
Можно ли вместо углов \( \displaystyle \alpha \) и \( \displaystyle \beta \) взять углы \( \displaystyle \varphi \) и \( \displaystyle \psi \)?
Конечно, можно!
Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет \( \displaystyle 180{}^\circ \).
Оставшиеся два угла тогда сами собой тоже дадут в сумме \( \displaystyle 180{}^\circ \). Не веришь? Давай убедимся.
Смотри:
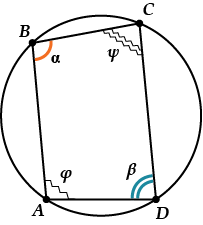
Пусть \( \displaystyle \alpha +\beta =180{}^\circ \). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, \( \displaystyle 360{}^\circ \).
То есть \( \displaystyle \alpha +\beta +\varphi +\psi =360{}^\circ \) — всегда! \( \displaystyle 180{}^\circ \)
Но \( \displaystyle \alpha +\beta =180{}^\circ \), →\( \displaystyle \varphi +\psi =360{}^\circ -180{}^\circ =180{}^\circ\).
Волшебство прямо!
Так что запомни крепко-накрепко:
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна \( \displaystyle 180{}^\circ \)
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна \( \displaystyle 180{}^\circ \), то такой четырехугольник вписанный.
Доказательство смотри чуть дальше.
А пока давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна \( \displaystyle 180{}^\circ \).
Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма?
Вписанный параллелограмм
Попробуем сперва «методом научного тыка»:
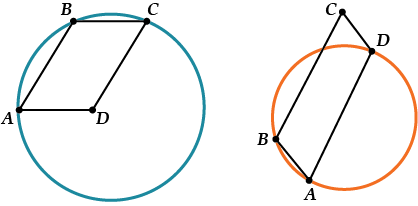
Вот как-то не получается. Теперь применим знание:

Предположим, что нам как-то удалось посадить на параллелограмм \( \displaystyle ABCD\) окружность. Тогда непременно должно быть: \( \displaystyle \alpha +\beta =180{}^\circ \), то есть \( \displaystyle \angle B+\angle D=180{}^\circ \).
А теперь вспомним о свойствах параллелограмма: у всякого параллелограмма противоположные углы равны.
То есть \( \displaystyle \angle B = \angle D\).
У нас получилось, что
\( \displaystyle \left\{ \begin{array}{l}\angle B=\angle D\\\angle B+\angle D=180{}^\circ \end{array} \right.\) → \( \displaystyle \left\{ \begin{array}{l}\angle B=90{}^\circ \\\angle D=90{}^\circ \end{array} \right.\)
А что же углы \( \displaystyle A\) и \( \displaystyle C\)?
Ну, то же самое конечно.
\( \displaystyle ABCD\) – вписанный → \( \displaystyle \angle A+\angle C=180{}^\circ \) → \( \displaystyle \angle A=90{}^\circ \)
\( \displaystyle ABCD\) — параллелограмм→ \( \displaystyle \angle A=\angle C\) → \( \displaystyle \angle C=90{}^\circ \)
Потрясающе, правда? Получилось, что…
Вписанная трапеция
А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция.
Почему?

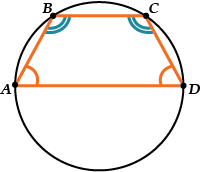
Вот пусть трапеция \( \displaystyle ABCD\) вписана в окружность.
Тогда опять \( \displaystyle \angle B+\angle D=180{}^\circ \), но из-за параллельности прямых \( \displaystyle AD\) и \( \displaystyle BC\) \( \displaystyle \angle B+\angle A=180{}^\circ \).
Значит, имеем: \( \displaystyle \left\{ \begin{array}{l}\angle B+\angle D=180{}^\circ \\\angle B+\angle A=180{}^\circ \end{array} \right.\) → \( \displaystyle \angle D=\angle A\) → трапеция равнобокая.
Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться:
Трапеция, вписанная в окружность – равнобедренная.
Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:
Главная теорема о вписанном четырехугольнике
Мы уже знаем, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность, что есть такая теорема:
Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна \( \displaystyle 180{}^\circ \).
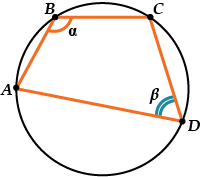
На нашем рисунке – \( \large\displaystyle \angle \alpha +\angle \beta =180{}^\circ \)
Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему.
Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.
Расшифровываем:
«Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна \( \displaystyle 180{}^\circ \)
«Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна \( \displaystyle 180{}^\circ \), то такой четырехугольник можно вписать в окружность
Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».
А теперь разбираемся, отчего же верно и 1, и 2?
Доказательство 1
Пусть четырехугольник \( \displaystyle ABCD\) вписан в окружность. Отметим её центр \( \displaystyle O\) и проведём радиусы \( \displaystyle OA\) и \( \displaystyle OC\).
Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального?
Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол».
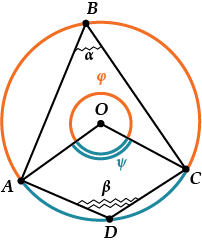
Итак,
Доказательство 2
Пусть оказалось так, что у четырехугольника \( \displaystyle ABCD\) сумма каких – то двух противоположных углов равна \( \displaystyle 180{}^\circ \). Скажем, пусть
\( \displaystyle \angle B+\angle D=180{}^\circ \)
Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника \( \displaystyle ABC\) мы гарантированно окружность описать можем. Так и сделаем это.
Если точка \( \displaystyle D\) не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.
Рассмотрим оба случая.
Пусть сначала точка \( \displaystyle D\) – снаружи.
Тогда отрезок \( \displaystyle AD\) пересекает окружность в какой-то точке \( \displaystyle E\). Соединим \( \displaystyle C\) и \( \displaystyle E\).
Получился вписанный (!) четырехугольник \( \displaystyle ABCE\).
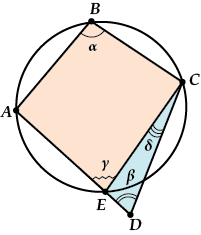
Следствие 1. Параллелограмм, вписанный в окружность, может быть только прямоугольником
Параллелограмм, вписанный в окружность, может быть только прямоугольником

Доказательство следствия 1
Давай-ка поймём, почему так. Пусть параллелограмм \( \displaystyle ABCD\) вписан в окружность. Тогда должно выполняться \( \displaystyle \angle B+\angle D=180{}^\circ \).
Но из свойств параллелограмма мы знаем, что \( \displaystyle \angle B=\angle D\).
То есть
\( \displaystyle \left\{ \begin{array}{l}\angle B+\angle D=180{}^\circ \\\angle B=\angle D\end{array} \right.\ \ \left\{ \begin{array}{l}\angle B=90{}^\circ \\\angle D=90{}^\circ \end{array} \right.\)
И то же самое, естественно, касательно углов \( \displaystyle A\) и \( \displaystyle C\).
Вот и получился прямоугольник – все углы по \( \displaystyle 90{}^\circ \).

Но, кроме того, есть ещё дополнительный приятный факт:
Центр окружности, описанной около прямоугольника, совпадает с точкой пересечения диагоналей.
Давай поймём почему. Надеюсь, ты отлично помнишь, что угол, опирающийся на диаметр – прямой.
Следствие 2. Трапеция, вписанная в окружность – равнобедренная
Трапеция, вписанная в окружность – равнобедренная

Докажем?
Пусть трапеция \( \displaystyle ABCD\) вписана в окружность. Тогда \( \displaystyle \angle B+\angle D=180{}^\circ \).
Но \( \displaystyle AD\parallel BC \Rightarrow \angle B+\angle A=180{}^\circ \)
То есть…
\( \displaystyle \left\{ \begin{array}{l}\angle B+\angle D=180{}^\circ \\\angle B+\angle A=180{}^\circ \end{array} \right.\) \( \displaystyle \Rightarrow \angle D=\angle A\). И так же \( \displaystyle \angle B=\angle C\).

«Секретный» способ распознавания вписанного четырехугольника
Всё ли мы обсудили?
Не совсем. На самом деле есть ещё один, «секретный» способ, как узнавать вписанный четырехугольник. Мы этот способ сформулируем не очень строго (но понятно).
Итак:
Если в четырёхугольнике можно наблюдать такую картинку, как здесь на рисунке (тут углы, «смотрящие» на сторону \( \displaystyle AD\) из точек \( \displaystyle B\) и \( \displaystyle C\), равны), то такой четырехугольник – вписанный.

Это очень важный рисунок – в задачах часто бывает легче найти равные углы, чем сумму углов \( \displaystyle B\) и \( \displaystyle D\).
Несмотря на совершенное отсутствие строгости в нашей формулировке, она верна, и более того, всегда принимается проверяющими ЕГЭ. Ты должен писать примерно так:
«\( \displaystyle \angle ABD=\angle ACD\Rightarrow ABCD\) — вписанный» — и всё будет отлично!
Не забывай этот важный признак – запомни картинку, и, возможно, она тебе вовремя бросится в глаза при решении задачи.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



почему «Секретный» способ распознавания вписанного четырехугольника оставлен без док-ва?
Некоторые комментарии прошлых лет к этой статье:
Ольга
01 апреля 2019
Спасибо очень интересно почему авторы учебников не пишут это
Лариса
28 ноября 2019
Супер, ты классный!! Лариса, 70 лет, помогаю внуку. Большое спасибо. Как говорил Г.Сковорода : «Дурный не той, хто не знае, а той, хто не хоче знаты» (Прошу прощения за вольный украинский, но это оригинал)
Михаил Сергеевич Сычёв
21 апреля 2020
Грамотно все расписано и разложено по полочкам