Биссектриса угла
Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.
Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…
Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!
Приступим!
Биссектриса угла — коротко о главном
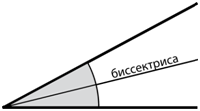
Биссектриса угла — это линия, делящая угол пополам.
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
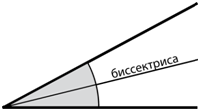
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
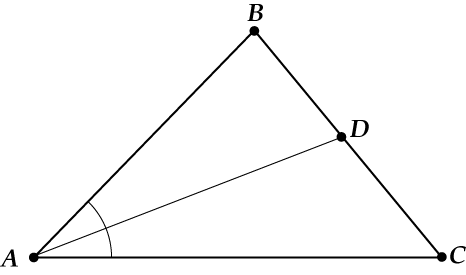
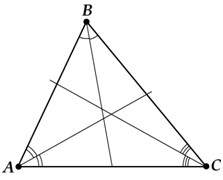
Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
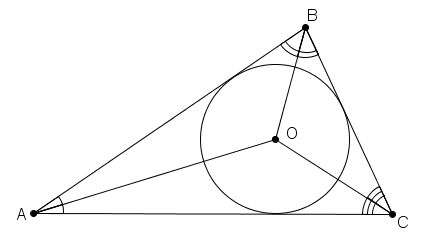
Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
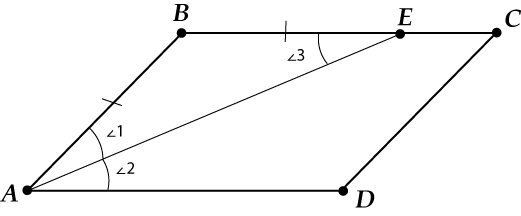
Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.
Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
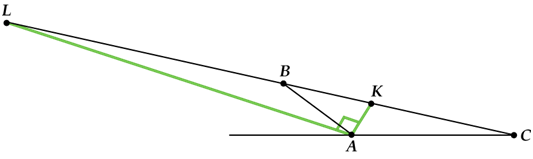
Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.


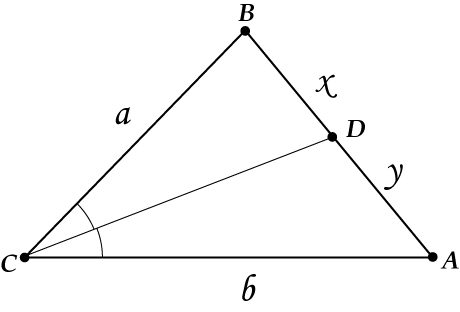
Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.
\( \displaystyle \frac{x}{y}=\frac{a}{b}\)
А теперь подробнее…
Определение биссектрисы угла
Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?
Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):
Биссектриса угла – это линия, делящая угол пополам.
Или еще вот такое определение биссектрисы:
Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.
А вот определение биссектрисы треугольника:
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.
Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.
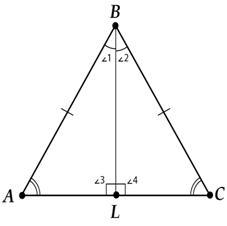
Биссектриса равнобедренного треугольника
Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.
Но представляешь, это ещё не всё. Верна ещё и обратная теорема:
Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.
Мы скоро докажем обе этих теоремы, а пока твердо запомни:
Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!
Зачем же это твердо запоминать? Как это может помочь?
А вот представь, что у тебя задача:
Дано: \( AB=5,~\angle ~ABD=~\angle DBC,~AD=DC. \)
Найти: \( \displaystyle BC. \)
Ты тут же соображаешь, \(\displaystyle BD \) биссектриса и, о чудо, она разделила сторону \( \displaystyle AC \) пополам! (по условию…).
Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.
Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!
Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике
Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?
Как это доказать?
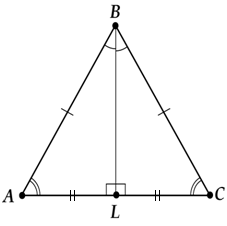
Смотри: у \( \triangle ABL \) и \( \triangle CBL \) равны стороны \( AB \) и \( BC \), сторона \( BL \) у них вообще общая и \( \angle 1=\angle 2\). (\( BL \) – биссектриса!)

И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.
Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что \( \triangle ABL=\triangle CBL \), а значит \( AL \)= \( CL \) и \( \angle 3=\angle 4 \).
\( AL \) = \( CL \) – это уже хорошо – значит, \( BL \) оказалась медианой.
А вот что такое \( \angle 3=\angle 4 \)?
Готов дальше?
Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.
Биссектриса, медиана, высота — определения и отличия
Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?
Если нет, не страшно. Сейчас разберемся.
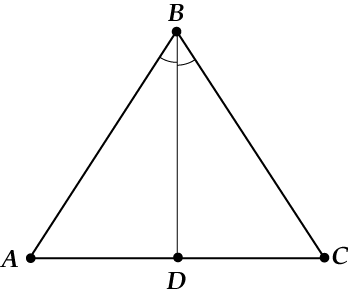
- Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно – это сторона \( AC. \);
- Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова \( AC \) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.;
- Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.
Чем биссектриса, медиана и высота похожи между собой?
Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.
Чем биссектриса, медиана и высота отличаются между собой?
- Биссектриса делит угол, из которого выходит, пополам.
- Медиана делит противоположную сторону пополам.
- Высота всегда перпендикулярна противоположной стороне.
Вернемся к нашим баранам — к свойствам биссектрисы…
Угол между биссектрисами любого треугольника
B \( \triangle ABC \)проведем две биссектрисы \( AO \)и \( OC \).
Они пересеклись. Какой же угол получился у точки \( O \)?
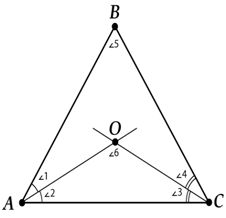
Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна \( 180{}^\circ \) ?
Применим этот потрясающий факт. С одной стороны, из \( \triangle ABC \):
\( \angle A+\angle B+\angle C=180{}^\circ \), то есть \( \angle B=180{}^\circ \text{ }-\text{ }\left( \angle A+\angle C \right) \).
Теперь посмотрим на \( \triangle AOC \):
\( \angle 2+\angle 6+\angle 3=180{}^\circ \)
Но биссектрисы, биссектрисы же!
\( \angle 2=\frac{\angle A}{2};\ \ \angle 3=\frac{\angle C}{2} \)
Значит \( \left( \triangle AOC \right) \)
\( \frac{\angle A}{2}+\angle 6+\frac{\angle C}{2}=180{}^\circ \), то есть
\( \angle 6=180{}^\circ -\frac{\angle A}{2}-\frac{\angle C}{2} \);
\( \angle 6=180{}^\circ -\frac{\angle A+\angle C}{2} \)
Вспомним про \( \triangle ABC : \angle A+\angle C=180{}^\circ -\angle B \)
Значит, \( \angle 6=180{}^\circ -\frac{180{}^\circ -\angle B}{2}=90+\frac{\angle B}{2} \)
Теперь через буквы
\( \angle AOC=90{}^\circ +\frac{\angle B}{2} \)
Не удивительно ли?
Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!
Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?
Или будет так:
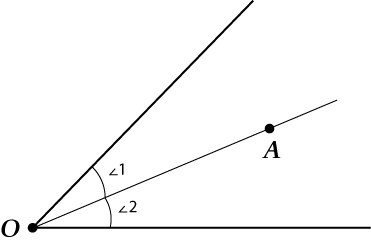
Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла
Ленивые математики как обычно в двух строчках спрятали четыре.
Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу два утверждения:
- Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
- Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.
Видишь разницу между утверждениями 1 и 2? Если не очень, то вспомни Шляпника из «Алисы в стране чудес»: «Так ты еще чего доброго скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», — одно и то же!»
Итак, нам нужно доказать утверждения 1 и 2, и тогда утверждение: «биссектриса – это геометрическое место точек, равноудаленных от сторон угла» будет доказано!
Почему же верно 1?
Возьмём любую точку на биссектрисе и назовём её \( \displaystyle A. \)
Опустим из этой точки перпендикуляры \( \displaystyle \) AB и \( \displaystyle AC \) на стороны угла.
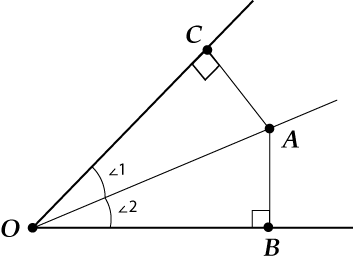
А теперь… Приготовились вспоминать признаки равенства прямоугольных треугольников! Если ты их подзабыл, то загляни в раздел «Прямоугольный треугольник».
Итак… Два прямоугольных треугольника: \( \displaystyle AOC \) и \( \displaystyle AOB. \) У них:
Почему же верно 2?
Возьмем какую-то точку \( \displaystyle E\) внутри угла, для которой расстояние до сторон угла равны.
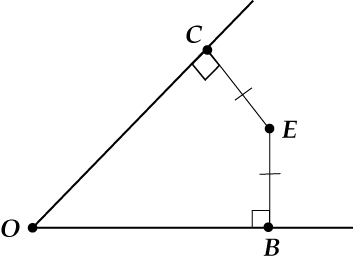
И соединим точки \( \displaystyle E\) и \( \displaystyle O\).
Теперь \( \displaystyle \triangle EOC=\triangle EOB\) как прямоугольные по катету и гипотенузе.
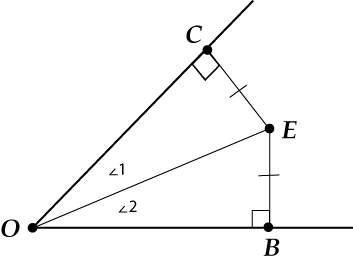
Значит, \( \displaystyle \angle 1=\angle 2\), то есть \( \displaystyle E\) лежит на биссектрисе!
Вот и всё!
Как же все это применить при решении задач? Вот например, в задачах часто бывает такая фраза: «Окружность касается сторон угла….». Ну, и найти нужно что-то.
То быстро соображаешь, что:
- Окружность касается сторон угла – значит, \( \displaystyle AC=AB\). (Правда, для этого нужно ещё знать, что радиус, проведённый в точку касания, перпендикулярен касательной)
- А раз \( \displaystyle AC=AB\), то \( \displaystyle AO\) – точно биссектриса!
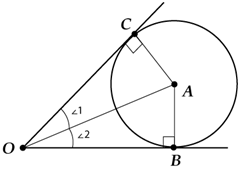
И можно пользоваться равенством \( \displaystyle \angle 1=\angle 2\).
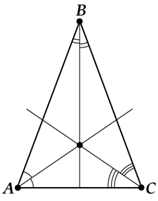
Три биссектрисы в треугольнике пересекаются в одной точке
Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:
Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.
Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?
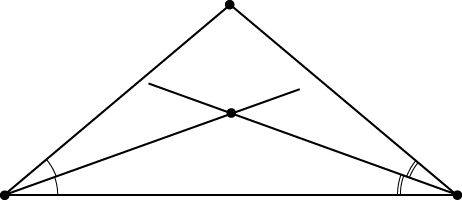
А третья биссектриса могла бы пройти так:
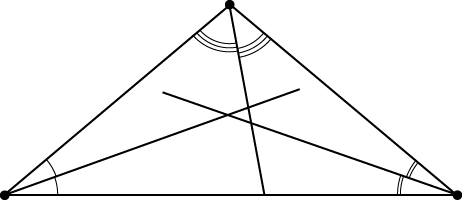
Но на самом деле-то всё гораздо лучше!
Давай рассмотрим точку пересечения двух биссектрис. Назовём её \( \displaystyle O\).
Эта точка лежит на биссектрисе \( \displaystyle AD\). Что из этого следует?
Правильно! \( \displaystyle OK=OM\)!
Точка \( \displaystyle O\) лежит ещё и на биссектрисе \( \displaystyle CE\), поэтому \( \displaystyle OK=ON\).
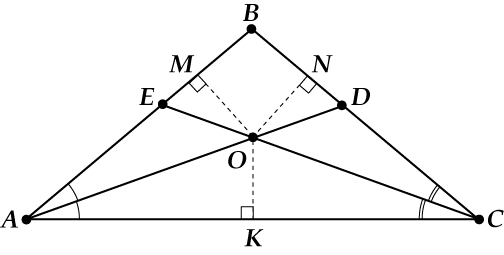
Что мы тут оба раза применяли?
Да пункт 1, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.
Вот и получилось \( \displaystyle OK=OM\) и \( \displaystyle OK=ON\).
Но посмотри внимательно на эти два равенства! Ведь из них следует, что:
Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.
Биссектриса и параллельность, биссектрисы смежных углов
Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например, некоторые из них:
Случай 1
Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Здорово, правда? Давай поймём, почему так.
С одной стороны, \( \displaystyle \angle 1=\angle 2\) — мы же проводим биссектрису!
Но, с другой стороны, \( \displaystyle \angle 2=\angle 3\) — как накрест лежащие углы (вспоминаем тему «Параллельные прямые»).
И теперь выходит, что:
Случай 2
Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.
Представь треугольник (или посмотри на картинку)
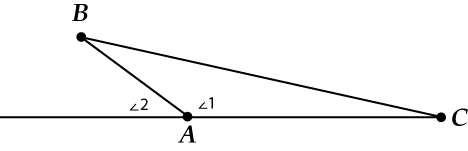
Давай продолжим сторону \( \displaystyle AC\) за точку \( A\). Теперь получилось два угла \( \displaystyle A\):
- \( \displaystyle \angle 1\) – внутренний угол \( \displaystyle \triangle ABC\)
- \( \displaystyle \angle 2\) – внешний угол \( \displaystyle \triangle ABC\) – он же снаружи, верно?
Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для \( \displaystyle \angle 1\), и для \( \displaystyle \angle 2\). Что же получится?

А получится прямоугольный \( \displaystyle \triangle ALK\)!
Удивительно, но это именно так.
Разбираемся.

Как ты думаешь, чему равна сумма \( \displaystyle \angle 1+\angle 2+\angle 3+\angle 4\)?
Случай 3
Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Видишь, что здесь все так же, как и для внутреннего и внешнего углов?

Или ещё раз подумаем, почему так получается?
Снова, как и для смежных углов,
\( \angle 1+\angle 2+\angle 3+\angle 4=180{}^\circ \) (как соответственные при параллельных основаниях).
И опять, \( \angle 2+\angle 3 \) составляют ровно половину от суммы \( \angle 1+\angle 2+\angle 3+\angle 4=180{}^\circ \)
Значит, \( \angle 2+\angle 3=90{}^\circ \).
Вывод:
Биссектриса и противоположная сторона
Оказывается, биссектриса угла треугольника делит противоположную сторону не как-нибудь, а специальным и очень интересным образом:
\( \displaystyle \frac{x}{y}=\frac{a}{b}\)
То есть:
Отношение отрезков, на которые биссектриса поделила сторону \( \displaystyle AB\), такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.
Удивительный факт, не правда ли?
Сейчас мы этот факт докажем, но приготовься: будет немного сложнее, чем раньше.

Снова – выход в «космос» — дополнительное построение!
Проведём прямую \( BK\parallel AC\).
Зачем? Сейчас увидим.

Продолжим биссектрису \( \displaystyle CD\) до пересечения с прямой \( \displaystyle BK\).
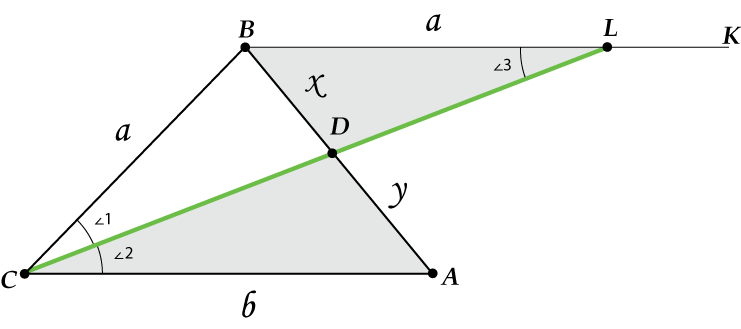
Знакомая картинка? Да-да-да, точно так же, как в пункте 4, случай 1 – получается, что \( \angle 1=\angle 2\) (\( \displaystyle CD\) – биссектриса)
\( \angle 2=\angle 3\) — как накрест лежащие
\( \Rightarrow \angle 1=\angle 3\) и \( BC=BL\)
Значит, \( BL\) – это тоже \( a\).
А теперь посмотрим на треугольники \( ACD\) и \( BLD\).
Что про них можно сказать?
Теперь можешь смело использовать! Разберём ещё одно свойство биссектрис углов треугольника. Самое сложное кончилось – будет проще.
Угол между биссектрисами треугольника
Пусть \( AO\) и \( CO\) – биссектрисы.
Найдём \( \angle AOC\) (помним, что сумма углов треугольника равна \( \displaystyle 180{}^\circ \)).
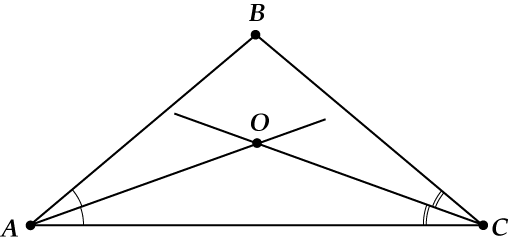
Получаем, что
\( \angle \text{ }\!\!~\!\!\text{ AOC}=90{}^\circ +\frac{\angle B}{2}\)
Это знание можно применить в тех задачах, где участвуют две биссектрисы и дан лишь угол \( B\), а искомые величины выдерживаются через \( \angle AOC\) или, наоборот, \( \angle AOC\) дан, а нужно найти что-то с участием угла \( B\).
Основные знания о биссектрисе закончились. Комбинируя эти факты, ты найдёшь ключ к любой задаче о биссектрисе!
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Алекс
05 января 2018
Отличное Объяснение! Всё подробно и понятным языком…Спасибо огромное!
Сабина
09 декабря 2018
Как же все аккуратно разложено по полочкам. Все доступно пониманию. Спасибо за ваш труд.
Данил
14 декабря 2019
Спасибо огромное