Касательные к окружности
В обычной жизни ты очень хорошо представляешь себе, что значит слово «коснуться».
И вот представь себе, в математике тоже существует такое понятие.
В этой теме мы разберёмся с выражениями «прямая касается окружности» и «две окружности касаются».
Касательные к окружности. Коротко о главном
Касательная – прямая, которая имеет с окружностью только одну общую точку.
Касательная окружности перпендикулярна радиусу, проведённому в точку касания.

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла: \( \displaystyle \angle CAB=\frac{1}{2}\angle AOB\), где:

Касание окружностей: если две окружности касаются, то точка касания лежит на прямой, соединяющей их центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей:
Внешнее касание
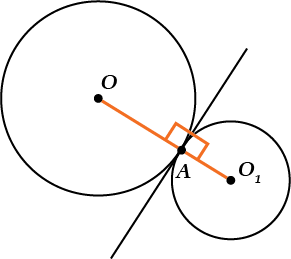
Внутреннее касание

Для двух окружностей с центрами \( \displaystyle {{O}}\) и \( \displaystyle {{O}_{1}}\), и радиусами \( \displaystyle R=OA\) и \( \displaystyle r={{O}_{1}}A\):
Касательные к окружности. Определения и основная теорема
Прямая касается окружности, если имеет с ней ровно одну общую точку.

Такая прямая называется касательной к данной окружности.
Посмотри-ка внимательно: очень похоже на жизнь, не правда ли? Прямая на картинке лишь чуть-чуть дотрагивается до окружности, касается ее.
Ну вот, и точно так же:
Две окружности касаются, если имеют ровно одну общую точку.

Что же тебе нужно знать о касательных и касающихся окружности?
Самая важная теорема гласит, что:
Радиус, проведённый в точку касания, перпендикулярен касательной.

Запомни это прямо как таблицу умножения! Все остальные факты о касательных и касающихся окружностях основаны именно на этой теореме.
Доказывать её мы здесь не будем, а вот как эта самая важная теорема работает, увидим сейчас несколько раз.
Угол между касательной и хордой
Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.

Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».
Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу.
То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!

Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.
Смотри, хорда \( \displaystyle AB\) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла \( \displaystyle BAC\), а другая дуга – внутри угла \( \displaystyle BAD\).

И теорема об угле между касательной и хордой говорит, что \( \displaystyle \angle CAB\) равен ПОЛОВИНЕ угла \( \displaystyle AOB\), \( \displaystyle \angle DAB\) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла \( \displaystyle AOB\).
При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?
Сейчас и увидим. \( \displaystyle OA\) – радиус, \( \displaystyle AC\) – касательная.
Значит, \( \displaystyle \angle OAC=90{}^\circ \).
Поэтому:\( \displaystyle \angle 1=90{}^\circ -\angle 4\).
Но \( \displaystyle \angle 2=\angle 1\) (\( \displaystyle OA\) и \( \displaystyle OB\) – радиусы)\( \displaystyle \angle 2=90{}^\circ -\angle 4\).
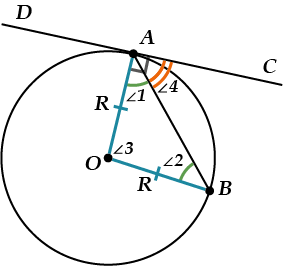
И осталось вспомнить, что сумма углов треугольника \( \displaystyle AOB\) равна \( \displaystyle 180{}^\circ \).
Пишем:
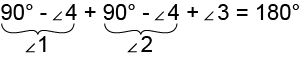
Короче:
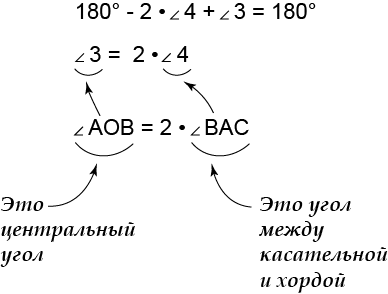
Здорово, правда? И самым главным оказалось то, что \( \displaystyle \angle OAC=90{}^\circ \).
Равенство отрезков касательных
Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:
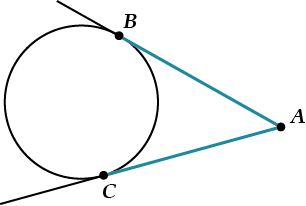
А ещё более удивительный факт состоит в том, что:
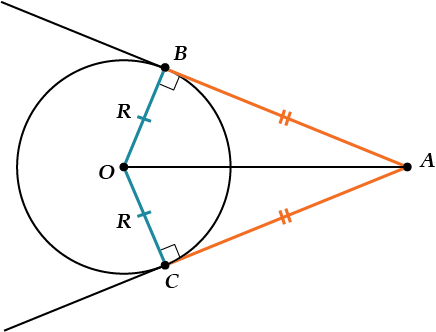
Отрезки касательных, проведённых из одной точки к одной окружности, равны.
То есть, на нашем рисунке, \( \displaystyle AB=AC\).
И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.
Вот, убедись.
Проведём радиусы \( \displaystyle OB\) и \( \displaystyle OC\) и соединим \( \displaystyle O\) и \( \displaystyle A\).
\( \displaystyle OB\) – радиус.
\( \displaystyle AB\) – касательная, значит, \( \displaystyle OB\bot AB\).
Ну, и так же \( \displaystyle OC\bot AC\).
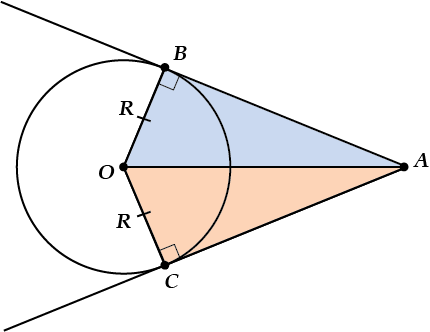
Получилось два прямоугольных треугольника \( \displaystyle AOB\) и \( \displaystyle AOC\), у которых:
\( \displaystyle \Rightarrow \Delta AOB\ =\ \Delta AOC\)(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).
Но раз \( \displaystyle \Delta AOB=\Delta AOC,\) то\( \displaystyle AB=AC\). УРА!

И ещё раз повторим – этот факт тоже очень важный:
Отрезки касательных, проведённых из одной точки, – равны.
И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.
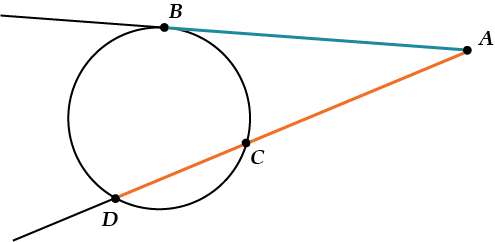
Для любой прямой \( \displaystyle AD\), пересекающей окружность,\( \displaystyle AD\cdot AC=A{{B}^{2}}\), где \( \displaystyle AB\) – отрезок касательной.

Хитроумными словами об этом говорят так:
«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».
Страшно? Не бойся, помни только, что в буквах это:
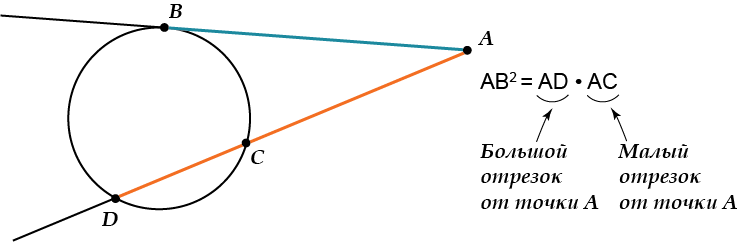
Общая касательная к двум окружностям
Прямая, которая касается двух окружностей, называется их общей касательной.

Общие касательные бывают внешние и внутренние. Смотри на картинки.
Две внутренние общие касательные:

Две внешние общие касательные:
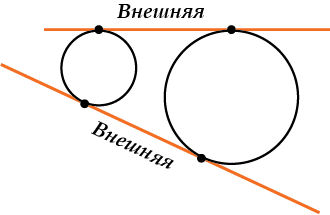
А всего – четыре! Не больше, но может быть меньше.
Вот так:
Есть только две внешние общие касательные.
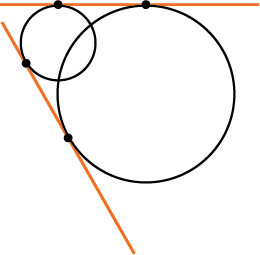
Или так: одна внутренняя и две внешних.

А может быть вообще так:
Только одна общая касательная.

И снова факты:
Длины отрезков двух внутренних общих касательных равны
Длины отрезков двух внешних общих касательных равны.
НО! При этом: внешние и внутренние касательные – разные! (а некоторых, может, и вообще нет…)
Касающиеся окружности
Касание окружностей бывает внешним и внутренним.
Вот такая картинка называется «окружности касаются внешним образом»:

А вот такая картинка называется «окружности касаются внутренним образом»:

Что же самое главное нужно знать?
Если две окружности касаются, то точка касания лежит на прямой, соединяющей центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей.

Если тебе показалось слишком длинно – посмотри картинку. Может быть ещё так:

Ура, теперь ты полностью вооружён на борьбу с касательными – дерзай! 🙂
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Камиль Богуцкий
15 октября 2017
Замечательно подобранный материал. Спасибо!
Александр Кель (админ)
15 октября 2017
Камиль, большое спасибо! Передам ваш отзыв автору этого материала Елене Евгеньевне Баштовой
Юлия Рябова
04 ноября 2017
Более толкового, полного, наглядного и потому очень понятного и доброжелательного объяснения, не встречала. Спасибо уважаемой Елене Евгеньевна. Браво.
Александр (админ)
04 ноября 2017
Юлия, огромное спасибо! Елене Евгеньевне, думаю, будет приятно слышать! )
Vufkan
07 ноября 2019
Спасибо вам вы очень помогли!
Александр (админ)
07 ноября 2019
Спасибо Vufkan! Очень рады! Заходи еще )
Еlen
22 января 2020
Привет из Латвии. Огромное спасибо за исчерпывающую информацию.
Александр (админ)
22 января 2020
Привет, Латвия! )) Спасибо, Elen. Очень приятно, что понравилось!