Квадратный корень — все, что нужно для сдачи ОГЭ и ЕГЭ
Зачем нужен квадратный корень? Очень хороший вопрос…
Попробуй на калькуляторе извлечь корень из трех.
Получается число, которое никогда не кончается: \( \sqrt{3}=1,732050807568\ldots \)
Как же такое число запомнить? А как его записать, если, допустим, нельзя округлять? Например на ЕГЭ?
Очень просто. С помощью квадратного корня. Пишешь \( \sqrt{3} \) и все.
Именно для упрощения записи таких чисел и было введено понятие квадратного корня. К слову такие числа называются иррациональными.
Ну и давай теперь разберемся с квадратным корнем…
Квадратный корень. Коротко о главном
Определение квадратного корня
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \( \displaystyle a\) называется такое неотрицательное число, квадрат которого равен \( \displaystyle a\).
Главное!
Если мы просто извлекаем квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Свойства арифметического квадратного корня
| СВОЙСТВО | ПРИМЕР |
|---|---|
| Корень произведения равен произведению корней: \( \displaystyle \sqrt[{}]{ab}=\sqrt[{}]{a}\cdot \sqrt[{}]{b}\) | \( \displaystyle \sqrt[{}]{64\cdot 9}=\sqrt[{}]{64}\cdot \sqrt[{}]{9}=8\cdot 3=24\) |
| Корень из дроби — это корень из числителя и корень из знаменателя: \( \displaystyle \sqrt[{}]{\frac{a}{b}}=\frac{\sqrt[{}]{a}}{\sqrt[{}]{b}}\), если \( \displaystyle a\ge 0\ ,\ b > 0\) | \( \displaystyle \sqrt[{}]{\frac{64}{9}}=\frac{\sqrt[{}]{64}}{\sqrt[{}]{9}}=\frac{8}{3}=2\frac{2}{3}\) |
| Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: \( \displaystyle {{\left( \sqrt{a} \right)}^{n}}={{\left( \sqrt{{{a}^{n}}} \right)}^{{}}}\), при \( \displaystyle a\ge 0\) | \( \displaystyle {{\left( \sqrt{2} \right)}^{4}}=\sqrt{{{2}^{4}}}=\sqrt{16}=4\) |
Что такое арифметический квадратный корень
Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа \(a\) называется такое неотрицательное число, квадрат которого равен \(a\). \( (\sqrt{a}=x,\ {{x}^{2}}=a;\ x,\ a\ge 0)\).
А почему же число \( a\) (число под корнем) должно быть обязательно неотрицательным?
Например, чему равен \( \sqrt{-9}\)?
Так-так, попробуем подобрать. Может, три?
Проверим: \( {{3}^{2}}=9\), а не \( -9\).
Может, \( \left( -3 \right)\)?
Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\).
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!
Число или выражение под знаком корня должно быть неотрицательным!
Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!
Ведь в определении сказано, что «квадратным корнем из числа\( a\)называется такое неотрицательное число, квадрат которого равен\( a\)».
Но подождите! В самом начале мы разбирали пример \( {{x}^{2}}=4\) и один из ответов был отрицательным числом!
Мы подбирали числа, которые можно возвести в квадрат и получить при этом \( \displaystyle 4\). Ответом были \( \displaystyle 2\) и \( \displaystyle -2\)
А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?
Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.
К примеру, \( \displaystyle {{x}^{2}}=4\) (квадратное уравнение) не равносильно выражению \( x=\sqrt{4}\) (арифмитический квадратный корень).
Из \( {{x}^{2}}=4\) следует, что
\( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2\); \( {{x}_{2}}=-2\)
(не помнишь почему так? Почитай тему «Модуль числа»!)
А из \( x=\sqrt{4}\) следует, что \( x=2\).
Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как \( 2\), так и \( x=-2\).
Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.
Наглядный пример разницы между квадратным уравнением и квадратным корнем
Этот наглядный пример привёл наш читатель Игорь, спасибо ему за это:
Пусть есть две ситуации:
1) \( x^2=64;\)
2) \( x= \sqrt{64}.\)
В первом случае у нас квадратное уравнение и его решением будет \( |х| =\sqrt{64}\) (уже видно отличие от второго случая) и далее получаем два корня \( x_1 = +8\text{ и }х_2 = -8.\)
Во втором случае у нас нет квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8.
Запись иррациональных чисел с помощью квадратного корня
А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.
Двигаемся дальше \( \displaystyle x=1\); \( \displaystyle {{1}^{2}}=1\) – меньше трех, тоже отметаем.
А что если \( \displaystyle x=2\)?
Проверим: \( \displaystyle {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( \displaystyle 1\) и \( \displaystyle 2\), а также между \( \displaystyle -2\) и \( \displaystyle -1\).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции \( \displaystyle y={{x}^{2}}\) и отметим на нем решения.

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!
Извлечем корень из \( \displaystyle 3\), делов-то!
Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568\ldots \) Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.
Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.
Еще один пример для закрепления
Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной \( \displaystyle 1\) км, сколько км тебе предстоит пройти?
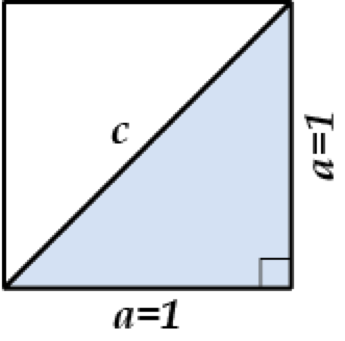
Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: \( {{c}^{2}}={{a}^{2}}+{{a}^{2}}\).
Таким образом, \( {{c}^{2}}=1+1=2\).
Так чему же здесь равно искомое расстояние?
Очевидно, что расстояние не может быть отрицательным, получаем, что \( c=\sqrt{2}\). Корень из двух приблизительно равен \( \displaystyle 1,41\), но, как мы заметили раньше, \( c=\sqrt{2}\) — уже является полноценным ответом.
Извлечение корней
Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.
Для этого необходимо знать, по меньшей мере, квадраты чисел от \( \displaystyle 1\) до \( \displaystyle 20\), а также уметь их распознавать.
То есть, тебе необходимо знать, что \( \displaystyle 15\) в квадрате равно \( \displaystyle 225\), а также, наоборот, что \( \displaystyle 225\) – это \( \displaystyle 15\) в квадрате.
Первое время в извлечении корня тебе поможет эта таблица.

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.
Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:
- \( \sqrt{0}=?\);
- \( \sqrt{64}=?\);
- \( \sqrt{121}=?\);
- \( \sqrt{289}=?\);
Ответы:
- \( \displaystyle 0\);
- \( \displaystyle 8\);
- \( \displaystyle 11\);
- \( \displaystyle 17\);
Ну как, получилось? Теперь давай посмотрим такие примеры:
- \( \sqrt{0,0196}=?\);
- \( \sqrt{0,0961}=?\);
- \( \sqrt{0,0144}=?\).
Ответы:
- \( \displaystyle 0,14\);
- \( \displaystyle 0,31\);
- \( \displaystyle 0,12\);
Свойства арифметического квадратного корня
Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:
- умножение;
- деление;
- возведение в степень.
Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:
| СВОЙСТВО | ПРИМЕР |
|---|---|
| Корень произведения равен произведению корней: \( \displaystyle \sqrt[{}]{ab}=\sqrt[{}]{a}\cdot \sqrt[{}]{b}\) | \( \displaystyle \sqrt[{}]{64\cdot 9}=\sqrt[{}]{64}\cdot \sqrt[{}]{9}=8\cdot 3=24\) |
| Корень из дроби — это корень из числителя и корень из знаменателя: \( \displaystyle \sqrt[{}]{\frac{a}{b}}=\frac{\sqrt[{}]{a}}{\sqrt[{}]{b}}\), если \( \displaystyle a\ge 0\ ,\ b > 0\) | \( \displaystyle \sqrt[{}]{\frac{64}{9}}=\frac{\sqrt[{}]{64}}{\sqrt[{}]{9}}=\frac{8}{3}=2\frac{2}{3}\) |
| Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: \( \displaystyle {{\left( \sqrt{a} \right)}^{n}}={{\left( \sqrt{{{a}^{n}}} \right)}^{{}}}\), при \( \displaystyle a\ge 0\) | \( \displaystyle {{\left( \sqrt{2} \right)}^{4}}=\sqrt{{{2}^{4}}}=\sqrt{16}=4\) |
Попробуем решить по несколько примеров на каждое свойство!
Умножение корней
Взглянул еще раз на табличку… И, поехали!
Начнем с простенького:
- \( \sqrt{5}\cdot \sqrt{3}=\sqrt{15}\)
- \( \sqrt{2}\cdot \sqrt{6}=\sqrt{12}\)
Минуууточку.
\( 12\) это \( \displaystyle 4\cdot 3\), а это значит, что мы можем записать вот так:
\( \sqrt{2}\cdot \sqrt{6}=\sqrt{12}=\sqrt{4\cdot 3}=\sqrt{4}\cdot \sqrt{3}=2\sqrt{3}\)Усвоил? Вот тебе следующий:
\( \displaystyle \sqrt{4}\cdot \sqrt{6}=2\cdot \sqrt{6}=2\sqrt{6}\)Корни из получившихся чисел ровно не извлекаются? Не беда – вот тебе такие примеры:
\( \displaystyle \sqrt{2}\cdot \sqrt{8}=\sqrt{16}=4\) \( \displaystyle \sqrt{12}\cdot \sqrt{3}=\sqrt{36}=6\)А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:
\( \displaystyle \sqrt{5}\cdot \sqrt{3}\cdot \sqrt{2}=\sqrt{10\cdot 3}=\sqrt30\)Теперь полностью самостоятельно:
- \( \displaystyle \sqrt{4}\cdot \sqrt{6}\cdot \sqrt{5}\)
- \( \displaystyle \sqrt{3}\cdot \sqrt{6}\cdot \sqrt{7}\)
- \( \displaystyle \sqrt{32}\cdot \sqrt{2}\)
Ответы:
- \( \displaystyle \sqrt{4}\cdot \sqrt{6}\cdot \sqrt{5}=\sqrt{4\cdot 6\cdot 5}=\sqrt{120}=\sqrt{4\cdot 30}=2\sqrt{30}\);
- \( \displaystyle \sqrt{3}\cdot \sqrt{6}\cdot \sqrt{7}=\sqrt{3\cdot 6\cdot 7}=\sqrt{126}\);
- \( \displaystyle \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8\).
Молодец! Согласись, все очень легко, главное знать таблицу умножения!
Деление корней
С умножением корней разобрались, теперь приступим к свойству деления.
Напомню, что формула в общем виде выглядит так:
\( \displaystyle \sqrt[{}]{\frac{a}{b}}=\frac{\sqrt[{}]{a}}{\sqrt[{}]{b}}\), если \( \displaystyle a\ge 0\ ,\ b>0\).
А значит это, что корень из частного равен частному корней.
Ну что, давай разбираться на примерах:
\( \displaystyle \frac{\sqrt{12}}{\sqrt{3}}=\sqrt{\frac{12}{3}}=\sqrt{4}=2\)Вот и вся наука. А вот такой пример:
\( \displaystyle \frac{\sqrt{12}}{3}=\frac{\sqrt{12}}{\sqrt{9}}=\sqrt{\frac{12}{9}}=\sqrt{\frac{4}{3}}=\frac{2}{\sqrt{3}}\)Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.
А что, если попадется такое выражение:
\( \displaystyle \sqrt{\frac{144}{225}}=?\)Надо просто применить формулу в обратном направлении:
\( \displaystyle \sqrt{\frac{144}{225}}=\frac{\sqrt{144}}{\sqrt{225}}=\frac{12}{15}=\frac{4}{5}=0,8\)А вот такой примерчик:
\( \displaystyle \sqrt{0,16}=\sqrt{\frac{16}{100}}=\frac{4}{10}=0,4\)Еще ты можешь встретить такое выражение:
\( \displaystyle \sqrt{5\frac{19}{25}}=?\)Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!
\( \displaystyle \sqrt{5\frac{19}{25}}=\sqrt{\frac{144}{25}}=\frac{12}{5}=2,4\)Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.
Возведение в степень
А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа \( \displaystyle a\) – это число, квадратный корень которого равен \( \displaystyle a\).
Так вот, если мы возводим число, квадратный корень которого равен \( \displaystyle a\), в квадрат, то что получаем?
Ну, конечно, \( \displaystyle a\)!
Рассмотрим на примерах:
\( \displaystyle {{\left( \sqrt{12} \right)}^{2}}=12\)
\( \displaystyle {{\left( \sqrt{17} \right)}^{2}}=17\)
Все просто, правда? А если корень будет в другой степени? Ничего страшного!
Придерживайся той же логики и помни свойства и возможные действия со степенями.
Забыл?
Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.
Вот, к примеру, такое выражение:
\( \displaystyle {{\left( \sqrt{5} \right)}^{6}}={{\left( {{\left( \sqrt{5} \right)}^{2}} \right)}^{3}}={{5}^{3}}=125\)В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:
\( \displaystyle {{\left( \sqrt{5} \right)}^{7}}={{\left( \sqrt{5} \right)}^{6}}\cdot \sqrt{5}=125\sqrt{5}\)С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:
\( \displaystyle \sqrt{{{3}^{2}}}=\sqrt{9}=3\)Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:
\( \displaystyle \sqrt{{{3}^{6}}}=\sqrt{{{\left( {{3}^{3}} \right)}^{2}}}={{3}^{3}}=27\)
\( \displaystyle \sqrt{{{3}^{5}}}=\sqrt{{{3}^{4}}\cdot 3}=\sqrt{{{\left( {{3}^{2}} \right)}^{2}}\cdot 3}={{3}^{2}}\cdot \sqrt{3}=9\sqrt{3}\)
Ну как, все понятно? Тогда реши самостоятельно примеры:
- \( \displaystyle \sqrt{{{\left( -3 \right)}^{2}}}\)
- \( \displaystyle \sqrt{{{6}^{6}}}\)
- \( \displaystyle {{\left( \sqrt{8} \right)}^{7}}\)
А вот и ответы:
Внесение под знак корня
Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!
Это совсем легко!
\( \displaystyle 4\sqrt{6}-2\sqrt{3}\cdot \sqrt{8}=\sqrt{16\cdot 6}-\sqrt{4\cdot 3\cdot 8}=\sqrt{96}-\sqrt{96}=0\)Допустим, у нас записано число \( \displaystyle 3\sqrt{5}\)
Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из \( \displaystyle 9\)!
\( \displaystyle 3\sqrt{5}=\sqrt{9}\cdot \sqrt{5}=\sqrt{45}\)Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:
\( \displaystyle 3\sqrt{10}-\sqrt{45}\cdot \sqrt{2}=\sqrt{90}-\sqrt{90}=0\)Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.
Реши самостоятельно вот этот пример — \( \displaystyle 4\sqrt{6}-2\sqrt{3}\cdot \sqrt{8}\)
Справился? Давай смотреть, что у тебя должно получиться:
\( \displaystyle 4\sqrt{6}-2\sqrt{3}\cdot \sqrt{8}=\sqrt{16\cdot 6}-\sqrt{4\cdot 3\cdot 8}=\sqrt{96}-\sqrt{96}=0\)Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!
Сравнение корней
Зачем нам учиться сравнивать числа, содержащие квадратный корень?
Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)
Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!
Например, определи, что больше: \( \displaystyle 3\sqrt{7}\) или \( \displaystyle 2\sqrt{17}\)?
Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?
Тогда вперед:
\( \displaystyle 3\sqrt{7}=\sqrt{9\cdot 7}=\sqrt{63}\) \( \displaystyle 2\sqrt{17}=\sqrt{4\cdot 17}=\sqrt{68}\)Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!
Т.е. если \( \displaystyle 68>63\), значит, \( \displaystyle \sqrt{68}>\sqrt{63}\).
Отсюда твердо делаем вывод, что \( \displaystyle 3\sqrt{7}<2\sqrt{17}\).
И никто не убедит нас в обратном!
Извлечение корней из больших чисел
До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!
\( \displaystyle \sqrt{98}=\sqrt{49\cdot 2}=\sqrt{49}\cdot \sqrt{2}=7\sqrt{2}\)Можно было пойти по иному пути и разложить на другие множители:
\( \displaystyle \sqrt{98}=\sqrt{7\cdot 14}\)Что дальше? А дальше раскладываем на множители до самого конца:
\( \displaystyle \sqrt{98}=\sqrt{7\cdot 14}=\sqrt{7\cdot 7\cdot 2}=\sqrt{{{7}^{2}}\cdot 2}=7\sqrt{2}\)Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.
Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:
\( \displaystyle \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}\)Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:
А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):
\( \displaystyle \sqrt{15}\cdot \sqrt{180}\cdot \sqrt{12}=\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}\)Разве это конец? Не останавливаемся на полпути!
\( \displaystyle \begin{array}{l}\sqrt{5\cdot 3}\cdot \sqrt{36\cdot 5}\cdot \sqrt{2\cdot 6}=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 12\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}=\\=\sqrt{5\cdot 3}\cdot \sqrt{3\cdot 2\cdot 2\cdot 3\cdot 5}\cdot \sqrt{2\cdot 3\cdot 2}\end{array}\)На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:
\( \displaystyle \begin{array}{l}\sqrt{5\cdot 3\cdot 3\cdot 2\cdot 2\cdot 3\cdot 5\cdot 2\cdot 3\cdot 2}=\sqrt{5\cdot 5\cdot 3\cdot 3\cdot 3\cdot 3\cdot 2\cdot 2\cdot 2\cdot 2}=\\=\sqrt{25}\cdot \sqrt{81}\cdot \sqrt{16}=5\cdot 9\cdot 4=180\end{array}\)Вот и все, не так все и страшно, правда?
\( \displaystyle \sqrt{15}\cdot \sqrt{54}\cdot \sqrt{10}=?\)Получилось \( \displaystyle 90\)? Молодец, все верно!
А теперь попробуй вот такой пример решить:
\( \displaystyle \sqrt{4225}=?\)А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.
Подготовка к ЕГЭ на 90+ в мини-группах
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



спасибо!
Пожалуйста, Алекс!
Большое спасибо! очень здорово написано! Все последовательно и понятно!
Я сейчас учусь в 10 классе и я очень благодарен за этот ваш сайт. Очень помогло. Спасибо большое.
Спасибо, Абдурахмон! Очень приятно слышать. Заходите к нам ещё.
хоть я и в 8 классе большое спасибо , очень помогли
Рожик, очень рады слышать! Кстати, учебник рассчитан и на 8 класс тоже, потому что каждая тема идет от простого к сложному. У нас есть ученики из 5-го класса )
Некоторые комментарии прошлых лет к этой статье:
Люба
13 ноября 2017
спасибо огромное очень помогли
Александр (админ)
13 ноября 2017
Люба, и тебе спасибо. Очень рады помочь!
илгар
21 августа 2019
спасибо очень понравилось отличная я сам с нуля изучаю физику физика самый классный предмет
Александр (админ)
21 августа 2019
Илгар, удачи в изучении физики. Физика очень интересный предмет!
Анна
13 ноября 2017
Спасибо. Я начала понимать алгебру благодаря вашему сайту !
Александр (админ)
13 ноября 2017
Анна, очень приятно слышать. Особенно нашим преподавателям, которые писали этот учебник Шевчуку Алексею Сергеевичу и Баштовой Елене Евгеньевне. Удачи, тебе на экзаменах.
Алевтина
15 ноября 2017
я работаю достаточно долго. а работа -ах как мне понравилась! спасибо!
Александр (админ)
15 ноября 2017
Отлично, Алевтина! Спасибо!
кыса
15 ноября 2017
шыкарнае обясненее. я сразу всё понила.
Александр (админ)
15 ноября 2017
СпасЫбо, Кыса! ))
БезгрАмАдный Оркадий
22 ноября 2017
шЫкарнА длА пАвтАрения перИт кАнтрольнАй))) А если нормально, но действительно годная теория))
Оликсандэр (админ)
23 ноября 2017
«Паффтарения» пишыца чириc дфа фэ… Спасибо! :))
Ирина
23 ноября 2017
СПАСИИИИБОО!!!!! 10 лет назад закончила учебу, а сейчас понадобилась математика вновь. Очень доходчиво и легко пишете. Огромное спасибо!
Александр
23 ноября 2017
Ничего себе! Через 10 лет понадобилась школьная математика? Мы рады, что помогло, Ирина.
Ксения
23 ноября 2017
Супер! Спасибо !
Александр (админ)
23 ноября 2017
Ксения, спасибо и тебе! Удачи на экзаменах!
сара
28 ноября 2017
спасибо…
Александр (админ)
28 ноября 2017
Пожалуйста, Сара!
28 ноября 2017
Благодарю:3 Очень помогло! Я не поняла корни на уроке, а тут просто и четко объяснили! Спасибо огромное)
Александр (админ)
28 ноября 2017
Очень рады, что помогло! Теперь если что не понятно, ты знаешь где искать простое и четкое объяснение 🙂 На youclever )
Нина
30 ноября 2017
Спасибо огромное! Думала репетитора придётся нанимать. Молодцы всё очень понятно!!!
Александр (админ)
30 ноября 2017
Пожалуйста, Нина. Очень приятно слышать такую оценку… но если захотите все-таки нанимать репетитора, посмотрите сначала наши курсы на 100gia.ru… Пишите )
Арсений
01 декабря 2017
Очень помогла теория и тут же закрепила практикой. Спасибо за понятную теорию!
Александр (админ)
01 декабря 2017
Рады слышать… Пожалуйста… (не знаю как обращаться, Арсений?). А где закрепляла практикой? Здесь же в учебнике? Или где-то еще. Вопрос не праздный… Очень надо знать.
Илья
08 декабря 2017
Всё очень понятно, но здесь к сожалению нет примеров, с которыми у меня возникают трудности: это когда под корнем ещё один корень( а под ним может быть ещё один, и т.д.).
Александр (админ)
10 декабря 2017
Илья, замечание принято. К сожалению мы не успеваем учитывать все, но вот какое объяснение я нашел на стороннем ресурсе. Может будет понятно… https://www.youtube.com/watch?v=5rntedrQ7NY
Алик
10 декабря 2017
Спасибо! За 10 минут я понял всю тему чем за 45 минут урока….
Александр (админ)
10 декабря 2017
Алик, как приятно слышать! Мы, вся команда, математики, консультанты, администраторы именно этого и добивались, чтобы было понятно за 10 минут. Удачи на экзаменах!)
Полина
12 декабря 2017
Очень доходчиво! Буду надеяться что сдам конторошку… Кстати не знаю нужно это вам или нет, НО мы сейчас час проходим такие примеры: Под корнем 17 в степени 2 минус 8 в степени 2(это на пример) В общем я думаю вам бы понадобилось и это записать)
Александр (админ)
12 декабря 2017
Полина, спасибо! Лучики тепла тебе и удачи ни контрошке… Может быть тебе будет интересно… у нас на 100gia.ru есть возможность за небольшие деньги купить «Тренировку по теме». Там по каждой теме много задач, с решениями и ответами моментальными и с объяснениями. Как раз чтобы подготовиться к конкретной контрошке (хорошее слово, кстати) 🙂
Алексей Шевчук
20 декабря 2017
Полина, посмотри в теме «Формулы сокращённого умножения» — разность квадратов: https://youclever.org/book/formuly-sokrashhennogo-umnozheniya-1#raznost-kvadratov
Юлька
19 декабря 2017
А про построение графиков с арифметическими корнями, если они возводятся в квадрат. y=(√x+3)^2+(√5-x)^2 при x>5 корень над всем выражением в скобках
Алексей Шевчук
21 декабря 2017
Юля, если корень возводится в квадрат, нужно написать ОДЗ и убрать корни вместе с квадратами. Если же это корень из квадрата выражения (то есть квадрат под корнем), то он превращается в модуль выражения.
Алла
22 декабря 2017
И все же. если в примере стоит корень из 64, то в ответе надо писать 8 или + — 8?
Игорь
22 декабря 2017
Насколько я понимаю есть две ситуации: 1) x^2=64. и 2) x= √64. В первом случае у нас квадратное уравнение и его решением будет «модуль х =√64» (уже видно отличие от второго случая) и, далее получаем два корня x1 = +8 и х2 = -8 Во втором случае у нас НЕТ квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда «одно неотрицательное число», то есть 8. (Это из определения корня, см выше)
Сергей
18 января 2018
Ответьте мне пожалуйста на 1 вопрос. Зачем он нужен этот квадратный корень? Я начинающий программист в школе учился хорошо, сейчас для общего развития решаю задачки со всякими алгоритмами в том числе с квадратным корнем. Чем умнее я становлюсь тем больше убеждаюсь что вся эта муть простому человеку нафиг не нужна ну серьёзно. Чтобы делать сайты не нужно быть математиком, я уже не говорю про гуманитариев, которые даже таблицу умножения могут не помнить уже. Так зачем всё это нужно?
Александр (админ)
18 января 2018
Хороший вопрос, Сергей ). По мне, так вопрос «Зачем?» самый важный и интересный. В особенности в математике. Ответ есть в нашем тексте. Почитайте внимательно. Математики люди ленивые и потому сообразительные. Чтобы записывать иррациональные числа более простым способом ввели понятие квадратного корня. Вот и все.
RedTea01
20 февраля 2018
Админ, спасибо за помощь)))
Александр (админ)
20 февраля 2018
Всегда рад! 🙂
Егор
21 февраля 2018
В школе ничего не понял, зашел на сайт и разобрал темы на 3 урока вперед. Спасибо вам, доходчиво и с подробными объяснениями.
Александр (админ)
21 февраля 2018
Егор, вот ради таких комментариев мы и работаем. ОЧЕНЬ приятно слышать всей нашей команде!
Светлана
12 марта 2018
Мне 72 , внучка задала вопрос по возведению в степень корня. Подзабыла. с удовольствием вспомнила. Спасибо з!амечательно
Александр
12 марта 2018
О как! Светлана, здравствуйте! Очень приятно слышать! Удачи Вашей внучке на экзаменах! )
Семён
13 мая 2018
А мне 77 лет. С удовольствием заполняю досуг, благо свободного времени хватает. И такое удовольствие получаю. Вот бы так учили в мои школьные годы. Израиль
Александр (админ)
13 мая 2018
Вот это комментарий!!! Семен, это ОЧЕНЬ приятно слышать. У нас были сомнения о том, как писать учебник: как обычно или «человеческим» языком. Видимо мы нашли правильный способ подачи материала. Спасибо Вам и отличного времяпровождения )
Александр
14 марта 2018
Ребята Огромное спасибо, я после армии, нужно сдать экзамен)) вы очень помогли!!!
Александр (админ)
14 марта 2018
Привет, Александр. Приятно слышать. Сам через это проходил: сдавал вступительные экзамены в институт (тогда ЕГЭ не было) после армии. Это очень трудно. Удачи на экзаменах.
Евгения
04 мая 2018
Спасибо огромное! Всё очень понятно и даже увлекательно) Кажется я начинаю любить математику:З
Александр (админ)
04 мая 2018
Ого! Евгения, это то, на что даже мы не рассчитывали! 🙂 На самом деле очень приятно… Удачи тебе с математикой. Она не такая и страшная, правда ведь? )
Шерзод
01 ноября 2018
Добрый день! Есть вопросы?
Сергей.
05 ноября 2018
Спасибо Вашей программе. Мне 72 , решил помочь внуку и чтобы не выглядеть неучем , вошел в вашу программу освежить немножко то что забыл. Объяснение очень доходчиво . СПАСИБО!
Александр (админ)
05 ноября 2018
Сергей, спасибо Вам! Очень ценно для нас слышать такие отзывы. Мы старались написать программу так, чтобы люди без подготовки и без знаний математики смогли ее понять. Удачи Вам и Вашему внуку.
Рам
02 декабря 2018
Вообще клево , инфа не теряет свойств со временем 🙂 Надо глянуть , что у вас тут еще есть по корням и теме , к ним прилежащей !
Александр (админ)
02 декабря 2018
Спасибо, Рам!
лол
17 января 2019
Спосыба аграмнае, очинь панятна
Александр (админ)
17 января 2019
Пажылуста ни мение агромнае!
SpaceJumpsuit
03 февраля 2019
Я уже 2 года учусь только по вашему сайту, ибо школа нормально ничего не объясняет. Снимаю шляпу перед YouClever… Спасибо, спасибо, спасибо.
Александр (админ)
03 февраля 2019
Вау!!! Вот это да! Очень! Очень приятно!
Алина
11 февраля 2019
Сайт-офигенный, вот реально, всё понятно, мне оч нравится, спасибо Вам большое от души
Александр (админ)
11 февраля 2019
Алина, спасибо огромное! Лучики тепла тебе!))
Генадий
11 февраля 2019
И всё же, из сказанного (К примеру, x2=4×2 =4 не равносильно выражению x=4–x=√4)(вставилось с искажениями), всё равно в итоге приходим к двум значениям корня из положит. числа. Другое дело, что разбирая свойства корней, возникает необходимость преимущественно оперировать только положительным значением корня. А потому и привели их к положит. значению через абсолютную величину. Так, в примере — корень из 64 * из 9 = 8*3=24 оперировать попеременно и с отриц .значениями не получится. Сказанное настоятельно не утверждаю, просто в качестве рассуждения. Всё же как-то трудновато для понимания как бы неприемлемость отриц. значения при извлечении кв. корня из числа. А вот свойства, да, получаются без ограничений только для положительных корней. А потому оперируем только ариффметическими при преобразовании выражений.
Алексей
11 февраля 2019
Геннадий, это хороший вопрос, который в рамках школьной программы, к сожалению, не разбирается. Вы можете посмотреть ответ на подобный вопрос в этом видео: https://www.youtube.com/watch?v=w9wPMMapKIQ
Сергей
19 февраля 2019
Ваш сайт единственный который смог достучаться до меня (в плане алгебры).
Александр (админ)
19 февраля 2019
Это очень… приятно слышать, Сергей. Удачи, на экзамене!
Викп
20 февраля 2019
Спасибо огромное за теорию. Очень понятно и доходчиво написано, разобрала все за минут 40-50~
Александр (админ)
20 февраля 2019
Спасибо, Викп! Была бы у меня возможность ставить смайлики, поставил бы довольную рожицу! 🙂
Павел
26 февраля 2019
Спасибо большое, все понял…почти. Вы написали что для того что бы вычислить квадратный корень из большого числа нужно разложить его на множители но как например разложить на множители такие крупные числа как 11234 3345 и т.д если таблицы квадратов на экзамене не будет+ очень трудно будет ее запомнить с11по 99)). Есть совет как быстро разложить такие большие числа на множители?
Александр (админ)
27 февраля 2019
Спасибо, Павел. Если коротко, то нужно знать две вещи: 1) что такое простое число 2) признаки делимости чисел(наизусть) и затем делить большое число на наименьший простой делитель (кроме единицы) без остатка, в столбик, до тех пор пока не останется 1. В вашем примере, используя признаки делимости определяем на какое наименьшее простое число делится 112 343 345. На 2? Нет. На 3? Сумма цифр числа не делится на 3. Значит нет. На 5? Да! Делим на 5 в столбик и получаем 22 468 669…. Опять вспоминаем признаки делимости. На какое наименьшее простое число делится уже новое число? И вот тут интересно…оно не делится без остатка ни на одно простое число. Это мы определяем по признакам делимости. Значит оно само — уже простое число. Мы можем разделить его только на 1 или на само себя. Вот мы и разложили ваше большое число на два множителя: 5 и 22 468 669…. Если я нигде не ошибся )) Ну, думаю, идею вы поняли. Признаки делимости можно посмотреть здесь: https://youclever.org/book/razlozhenie-na-mnozhiteli-2 Их надо выучить назубок.
Александр (админ)
27 февраля 2019
Павел, вот здесь наглядно очень про то, как раскладывать на множители большие числа: https://ru.wikihow.com/разложить-число-на-множители
Игорь
17 марта 2019
Спасибо коллективу авторов и участникам проекта! Понятное объяснение на примерах!
Александр (админ)
17 марта 2019
Приятно слышать, Игорь!
Сергей
27 марта 2019
присвоили ему специальный символ √. Этот символ имеет собственное название — РАДИКАЛ. Хорошие у Вас лекции. Скажите, а в комментах можно пользоваться HTML-кодом? Все-таки на что -то читатель хочет обратить внимание — процитировав, где-то использовать курсив итп
Александр (админ)
27 марта 2019
К сожалению нет. Но идея хорошая. Может быть прикрутим редактор к коментариям.
Сергей
15 апреля 2019
Очень жаль, что не читаете комментарий. В тексте написано: «присвоили ему специальный символ √.» Было предложено дописать: «присвоили ему специальный символ √(радикал).» Это, что ухудшит текст?
Александр (админ)
15 апреля 2019
Сергей, я прочитал комментарий, но не понял, что это было предложение ). Не обижайтесь, но я его не принял. Мы старались облегчить тексты для понимания. Если дать сразу все определения слова «радикал» — это не поможет разобраться, наоборот запутает. Ведь тогда надо говорить, что радикал — это еще и значение числа, извлекаемого из квадратного корня, а так же значение выражения извлекаемого из квадратного корня, что это «не тот радикал, что бросает бомбы», ну и так далее. Определение символа добавляет не много смысла, но утяжеляет текст и отвлекает от основного понятия. На мой взгляд учебники математики для школьников этим грешат: даются сразу все определения, причем строгие… Но так никто не учится. В том числе и те, кто пишет эти учебники. Их учили не так. Им в детстве вводили понятия не сразу все, а последовательно и давали возможность встроить понятия в свою картину мира, своими словами. А уж потом давали строгие определения… В общем без обид :)) Я не буду перегружать текст.
Сергей
15 апреля 2019
Был бы тег и догадываться не пришлось бы. 🙂 Не обижайтесь, но все последующии доводы в ответе — говорят о том, что вы не в курсе почему у знака радикал две полки ( речь в данном случае не о том, что маленькая для степени, большая для «содержимого») . Речь об истории возникновения данного символа и его фундаментально значения для понимания — ЧИСЛА. Но это тема для отдельной беседы. С уважением.
Александр (админ)
30 мая 2019
Сергей, спасибо еще раз за предложение сделать html код. Дай бог дойдут руки… Но предложение правда хорошее. По сути предмета — я не математик ) Эти лекции писал не я.
Даня
30 мая 2019
спасибо за информацию. без нее я бы не написал реферат и не получил бы итоговую
Александр Кель (админ)
30 мая 2019
Даня! Приятно слышать! Мои поздравления с итоговой оценкой! Так держать! 🙂
Anubis
07 июня 2019
Ужасный сайт всё платное плохо всё расписано просто —
Александр (админ)
12 июня 2019
Anubis, а что конкретно «плохо расписано»? По поводу платности контента. Для меня весь контент сайта платный. Мне пришлось заплатить математикам, которые его писали, довольно приличную сумму. А для пользователей сайта 90% конетнта бесплатно. Вы разве не заметили? За оставшиеся 10% я беру деньги и они идут на поддержание сайта. Кстати, Anubi, не хотите бесплатно поработать над созданием контента или еще над чем-нибудь для сайта? Что вы умеете? Работы много…
Александр
16 июня 2019
Можете пояснить следующий момент. Вы пишете, что корень из числа имеет 2 варианта ответа (например корень из 4 это +2 и -2) только если решается уровнениенеравенство, а если ПРОСТО извлечь корень из числа то только положительное число. Но получается какая-то несостыковка: при решении иррациональных УРАВНЕНИЙ принимают как подкоренное выражение не должно быть отрицательным, но так и корень >= 0. Вроде и решение уравнения и в тоже время просто извлечение корня и все одновременно. 🙁
Алексей Шевчук
30 июня 2019
Александр, корень из числа имеет только один вариант ответа (в рамках действительных чисел — комплексных чисел в школьной программе нет, а если даже есть, то в условии задачи явно говорят, что комплексные корни нас тоже интересуют). Два варианта ответа возникает не при извлечении корня и не при решении иррациональных уравнений, а при решении квадратных уравнений, то есть тех, где неизвестная была в квадрате, а не под корнем.
Дима
19 июня 2019
Спасибо огромное за помощь в математике
Александр (админ)
20 июня 2019
Дима, рады, что смогли помочь. Удачи на всех экзаменах!
Ирина
19 июня 2019
Можете пожалуйста на вопрос. Вот корень из х^2+1 можно разложить на 2 корня? Корень из х^2 + корень из 1?
Александр (админ)
20 июня 2019
Нет, Ирина, так нельзя делать. Смотри, как только ты видишь «икс в квадрате» перед тобой квадратное уравнение. Твое уравнение квадратное. Но оно неполное, потому что нет еще одного икса… Вот как решаются неполные квадратные уравнения. Посмотри это видео вдумчиво,. с паузами и ты все поймешь. https://www.youtube.com/watch?v=CtgP34y-uOI
Вадик 5,5лет детский садик нумер 8
03 июля 2019
Очинь панравился
Александр (пдмин)
03 июля 2019
Какой молодец, Вадик! Такие взрослые книги читаешь в 5,5 лет!
Я
16 июля 2019
Посмотрим-посмотрим
Ирина
16 августа 2019
В какой последовательности решается 8÷3√5
Алексей Шевчук
17 августа 2019
Ирина, а что именно нужно решить? Предположу, что избавиться от иррациональности в знаменателе, тогда нужно числитель и знаменатель домножить на √5. Тогда два корня в знаменателе дадут просто 5, и останется 8√5÷15 (корень переехал в числитель).
Огрызок Яблока
21 октября 2019
Нормальный такой сайт. Не, ну реально бОмБа)))0), а админи какие добрые. Даже такой овощь как я понял, моё увожение
Александр (админ)
21 октября 2019
Круто, уважаемый Огрызок Яблока. Я, например, очень жалею, что в мое время такого сайта не было. Спасибо и удачи!
Сергей
09 ноября 2019
Почему в блоке Возведение в степень, у вас в 1 задании √(−3)^2 а должно же быть неотрицательным.
Алексей Шевчук
09 ноября 2019
Сергей, (−3)^2=9 — число положительное. Квадрат всё делает положительным. Но нужно быть внимательным: если квадрат за пределами корня, то его магия уже не работает: (√(−3))^2 — здесь мы сначала пытаемся извлечь корень из (-3) и всё ломается.
Диля
10 ноября 2019
Спасибо большое, всё понятно и простым языком!!!
Александр (админ)
10 ноября 2019
Спасибо, Диля, от меня и Алексея Шевчука. Рады, что понравился текст.
Хадижат
26 ноября 2019
Спасибо, всё объяснили всё поняла
Александр (admin)
26 ноября 2019
Пожалуйста, Хадижат! Успехов!
Ася
26 ноября 2019
Спасибо большое! Вы ОЧЕНЬ помогли! Я на больничном, поэтому такую важную тему пропустила, а догонять как-то надо и вот случайно зашла на ваш сайт!
Александр (админ)
26 ноября 2019
Ася, выздоравливай скорее! И спасибо тебе за теплые слова. Нам очень всем приятно. Надеемся, что эта тема в нашем учебнике улучшила тебе самочувствие во время болезни. Удачи на экзаменах!
Юрий
26 ноября 2019
Объясните пожалуйста. Уравнение в школьной программе x²-12x-24=0. корни получаются 6+2√15 и 6+2√15, подставляю корни в уравнение, но 0 ни как не получается, про теорему Виета вообще молчу. во всех уравнениях сумма корней x1 и x2 никак не сходится с произведением х1 и х2? Сейчас смотрю в учебник. Сумма -9, произведение -22 или сумма 1, произведение -72… как это, ни одного примера чтоб эта теорема работала.
Алексей Шевчук
27 ноября 2019
Юрий, корни получаются 6+2√15 и 6-2√15 — то есть один из корней с минусом. Не знаю, была это опечатка, или один из корней получился неверным, но какой из них ни подставь в уравнение, всё равно получится 0, например: (6+2√15)^2-12*(6+2√15)-24=6^2+2*6*2√15+(2√15)^2 — 12*6 — 12*2√15 — 24 = 0. Что касается теоремы Виета, мне кажется, ты её неправильно понял: x1+x2 не должно быть равно x1*x2. Сумма корней должна равняться коэффициенту перед х в первой степени с обратным знаком (то есть в данном случае коэффициент равен -12, тогда x1+x2=12), а произведение корней — свободному члену, то есть слагаемому без х (в нашем случае это x1*x2=-24). Проверь ещё раз: и сумма, и произведение корней дают нужные числа.
Ирина
02 декабря 2019
все хорошо, но не написали как решать такие примеры: 9-корень из 21 (нет знака корень на клавиатуре)
Алексей Шевчук
03 декабря 2019
Ирина, это тема «Квадратный корень» — то есть (по определению) корень степени 2. Если Вам нужны корни более высокой степени, добро пожаловать в тему «Степень и её свойства»: https://youclever.org/book/stepen-i-ee-svojstva-1 — ищите там раздел «степень с рациональным показателем».
Максим
15 декабря 2019
Спасибо вам огромное! Я в 6 классе, но мне очень интересно как вычислить корень у того или иного числа! Срасибо еще раз! Вы для меня прямо открыли целый мир алгебры!)
Александр (админ)
15 декабря 2019
Очень приятно слышать, Максим! Ты большой молодец, что в 6-и классе читаешь учебники, предназначенные для 8-го — 11-го класса!
лера
17 декабря 2019
статья чупер алгебра легко дается спасибо)))) а у вас есть формулы сокращенного умножения?
Александр (админ)
17 декабря 2019
Конечно, есть, Лера. Все темы математики для подготовки к ОГЭ и ЕГЭ есть. В сокращенном варианте бесплатно и в полном варианте для учеников YouClever. Но я советую тебе зарегистрироваться на сайте, через пункт меню «Войти» и у тебя будет доступ к 5 темам математики в полном варианте бесплатно. Одна из тем — темы сокращенного умножения. Там есть все что нужно, чтобы разобраться. Даже примеры для тренировки.
Кирилл
20 марта 2020
Спасибо очень помогли!
Александр (админ)
20 марта 2020
Пожалуйста, Кирилл! Удачи на экзамене!
Матвей
26 марта 2020
Спасибо,но хотелось бы увидеть по больше примеров,а так,информация довольно понятна даже таким как я.
Александр (админ)
26 марта 2020
Пожалуйста, Матвей. Хорошо, что во всем разобрался. Приходи еще)
Ильнара
04 апреля 2020
Спасибо вам, наконец я поняла эту тему. Ураа
Александр (админ)
04 апреля 2020
Ильнара, ты умница! Удачи тебе на всех жизненных экзаменах!
даня
16 апреля 2020
спасибо хорошее объяснениие у меня во фторник был экзамен и мне эта тема пригадилась
Александр (админ)
16 апреля 2020
Спасибо, Даня! Рады, что ты справился с экзаменом.
Тоха
16 июня 2020
сайт просто топ) спасибо)))))))))))))))))))))))))) сдал еге на чистую 5)))))))))))))))))) спасибо)))))))))))))))))
админыч)
23 июня 2020
неплохо объяснили , осталось вспомнить , как решать квадратные выражения типа 0,5 корней из 1600-1/3 умноженное на корень из 36
Алексей Шевчук
23 июня 2020
Ну а что там вспоминать. 1) Чему равен корень из 1600? Умножаем это на 0,5. 2) Чему равен корень из 36? Умножаем на 1/3. Потом вычитаем из первого второе.
В этом комментарии я собрал отзывы о нашей работе за разные годы:
Люба, 13 ноября 2017
спасибо огромное очень помогли
илгар
21 августа 2019
спасибо очень понравилось отличная я сам с нуля изучаю физику физика самый классный предмет
Анна
13 ноября 2017
Спасибо. Я начала понимать алгебру благодаря вашему сайту !
Алевтина
15 ноября 2017
я работаю достаточно долго. а работа -ах как мне понравилась! спасибо!
Александр (админ)
15 ноября 2017
Отлично, Алевтина! Спасибо!
кыса
15 ноября 2017
шыкарнае обясненее. я сразу всё понила.
БезгрАмАдный Оркадий
22 ноября 2017
шЫкарнА длА пАвтАрения перИт кАнтрольнАй))) А если нормально, но действительно годная теория))
Ирина
23 ноября 2017
СПАСИИИИБОО!!!!! 10 лет назад закончила учебу, а сейчас понадобилась математика вновь. Очень доходчиво и легко пишете. Огромное спасибо!
Ксения
23 ноября 2017
Супер! Спасибо !
28 ноября 2017
Благодарю:3 Очень помогло! Я не поняла корни на уроке, а тут просто и четко объяснили! Спасибо огромное)
Нина
30 ноября 2017
Спасибо огромное! Думала репетитора придётся нанимать. Молодцы всё очень понятно!!!
Арсений
01 декабря 2017
Очень помогла теория и тут же закрепила практикой. Спасибо за понятную теорию!
Алик
10 декабря 2017
Спасибо! За 10 минут я понял всю тему чем за 45 минут урока….
Полина
12 декабря 2017
Очень доходчиво! Буду надеяться что сдам конторошку…
Александр
11 февраля 2018
Здравствуйте! Очень много полезной информации! СПАСИБО!
RedTea01
20 февраля 2018
Админ, спасибо за помощь)))
Егор
21 февраля 2018
В школе ничего не понял, зашел на сайт и разобрал темы на 3 урока вперед. Спасибо вам, доходчиво и с подробными объяснениями.
Светлана
12 марта 2018
Мне 72 , внучка задала вопрос по возведению в степень корня. Подзабыла. с удовольствием вспомнила. Спасибо з!амечательно
Семён
13 мая 2018
А мне 77 лет. С удовольствием заполняю досуг, благо свободного времени хватает. И такое удовольствие получаю. Вот бы так учили в мои школьные годы. Израиль
Александр
14 марта 2018
Ребята Огромное спасибо, я после армии, нужно сдать экзамен)) вы очень помогли!!!
Евгения
04 мая 2018
Спасибо огромное! Всё очень понятно и даже увлекательно) Кажется я начинаю любить математику
Сергей.
05 ноября 2018
Спасибо Вашей программе. Мне 72 , решил помочь внуку и чтобы не выглядеть неучем , вошел в вашу программу освежить немножко то что забыл. Объяснение очень доходчиво . СПАСИБО!
Рам
02 декабря 2018
Вообще клево , инфа не теряет свойств со временем 🙂 Надо глянуть , что у вас тут еще есть по корням и теме , к ним прилежащей !
лол
17 января 2019
Спосыба аграмнае, очинь панятна
SpaceJumpsuit
03 февраля 2019
Я уже 2 года учусь только по вашему сайту, ибо школа нормально ничего не объясняет. Снимаю шляпу перед YouClever… Спасибо, спасибо, спасибо.
Алина
11 февраля 2019
Сайт-офигенный, вот реально, всё понятно, мне оч нравится, спасибо Вам большое от души
Сергей
19 февраля 2019
Ваш сайт единственный который смог достучаться до меня (в плане алгебры).
Викп
20 февраля 2019
Спасибо огромное за теорию. Очень понятно и доходчиво написано, разобрала все за минут 40-50~
Игорь
17 марта 2019
Спасибо коллективу авторов и участникам проекта! Понятное объяснение на примерах!
Даня
30 мая 2019
спасибо за информацию. без нее я бы не написал реферат и не получил бы итоговую
Дима
19 июня 2019
Спасибо огромное за помощь в математике
Огрызок Яблока
21 октября 2019
Нормальный такой сайт. Не, ну реально бОмБа)))0), а админи какие добрые. Даже такой овощь как я понял, моё увожение
Диля
10 ноября 2019
Спасибо большое, всё понятно и простым языком!!!
Хадижат
26 ноября 2019
Спасибо, всё объяснили всё поняла
Ася
26 ноября 2019
Спасибо большое! Вы ОЧЕНЬ помогли! Я на больничном, поэтому такую важную тему пропустила, а догонять как-то надо и вот случайно зашла на ваш сайт!
Максим
15 декабря 2019
Спасибо вам огромное! Я в 6 классе, но мне очень интересно как вычислить корень у того или иного числа! Срасибо еще раз! Вы для меня прямо открыли целый мир алгебры!)
лера
17 декабря 2019
статья чупер алгебра легко дается спасибо)))) а у вас есть формулы сокращенного умножения?
Кирилл
20 марта 2020
Спасибо очень помогли!
Ильнара
04 апреля 2020
Спасибо вам, наконец я поняла эту тему. Ураа
даня
16 апреля 2020
спасибо хорошее объяснениие у меня во фторник был экзамен и мне эта тема пригадилась
Тоха
16 июня 2020
сайт просто топ) спасибо)))))))))))))))))))))))))) сдал еге на чистую 5)))))))))))))))))) спасибо)))))))))))))))))