Описанная окружность (ЕГЭ 2022)
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника.
Что же это такое?
Давай разберемся!
Описанная окружность — коротко о главном
Определение
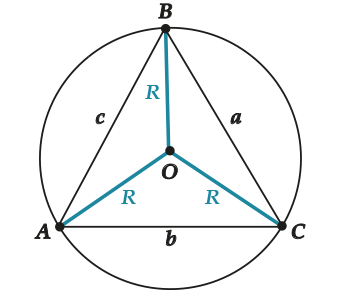
Окружность, описанная около треугольника – это окружность, которая проходит через все три вершины этого треугольника.
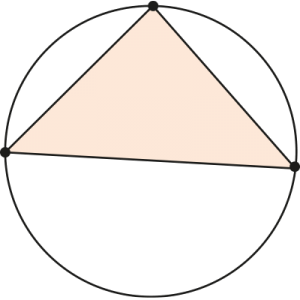
Центр описанной окружности
Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.

Радиус описанной окружности
\( \displaystyle \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\)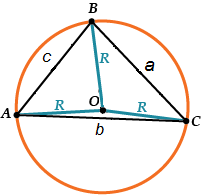
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
Расположение центра описанной окружности
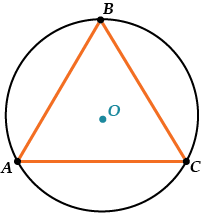
В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника
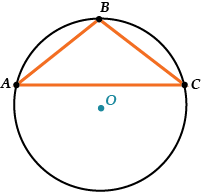
В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
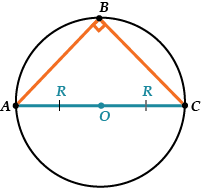
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.

Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!

И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
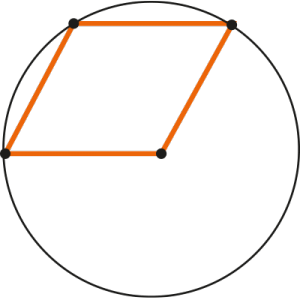
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
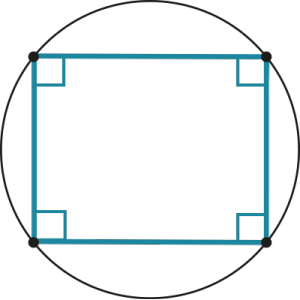
Подробнее об этом смотри в статье о вписанных четырехугольниках!
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
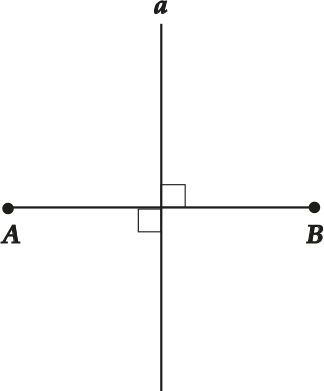
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая \( \displaystyle a\) – это серединный перпендикуляр к отрезку \( \displaystyle AB\).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке \( \displaystyle O\).
Это и есть центр описанной около (вокруг) треугольника \( \displaystyle ABC\) окружности.
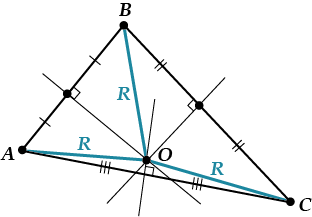
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
Вот так:
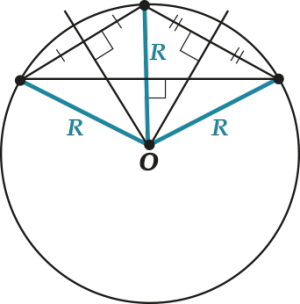
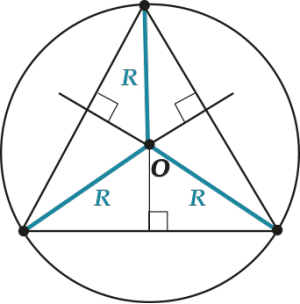
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Здорово, правда?
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
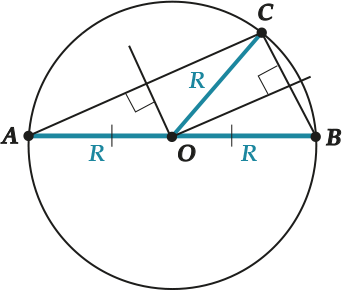
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
А именно:
В произвольном треугольнике:
\( \Large \displaystyle \frac{a}{\sin \angle A}=2R\)
Ну и, конечно,
\( \displaystyle \begin{array}{l}\frac{b}{\sin \angle B}=2R\\\frac{c}{\sin \angle C}=2R\end{array}\)
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Смотри, вот так:

Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «\( \displaystyle X\)» — такое множество точек, что все они обладают свойством «\( \displaystyle X\)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «\( \displaystyle X\)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему
Приступим:
Проверим 1. Пусть точка \( \displaystyle M\) лежит на серединном перпендикуляре к отрезку \( \displaystyle AB\).
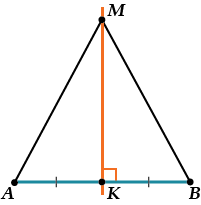
Соединим \( \displaystyle M\) с \( \displaystyle A\) и с \( \displaystyle B\).Тогда линия \( \displaystyle MK\) является медианой и высотой в \( \displaystyle \Delta AMB\).
Значит, \( \displaystyle \Delta AMB\) – равнобедренный, \( \displaystyle MA=MB\) – убедились, что любая точка \( \displaystyle M\), лежащая на серединном перпендикуляре, одинаково удалена от точек \( \displaystyle A\) и \( \displaystyle B\).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка \( \displaystyle M\) равноудалена от точек \( \displaystyle A\) и \( \displaystyle B\), то есть \( \displaystyle MA=MB\).

Возьмём \( \displaystyle K\) – середину \( \displaystyle AB\) и соединим \( \displaystyle M\) и \( \displaystyle K\). Получилась медиана \( \displaystyle MK\). Но \( \displaystyle \Delta AMB\) – равнобедренный по условию \( \displaystyle (MA=MB)\Rightarrow MK\) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка \( \displaystyle M\) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
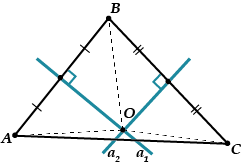
Рассмотрим треугольник \( \displaystyle ABC\). Проведём два серединных перпендикуляра \( \displaystyle {{a}_{1}}\) и \( \displaystyle {{a}_{2}}\), скажем, к отрезкам \( \displaystyle AB\) и \( \displaystyle BC\). Они пересекутся в какой-то точке, которую мы назовем \( \displaystyle O\).
А теперь, внимание!
Точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{1}}\Rightarrow OA=OB\);
точка \( \displaystyle O\) лежит на серединном перпендикуляре \( \displaystyle {{a}_{2}}\Rightarrow OB=OC\).
И значит, \( \displaystyle OA=OB=OC\) и \( \displaystyle OA=OC\).
Отсюда следует сразу несколько вещей:
Радиус описанной окружности
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме).
\( \displaystyle \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\)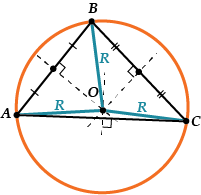
То есть:
\( \large\displaystyle \frac{\text{a}}{\sin \angle \text{A}}=2\text{R}\) и\( \large\displaystyle \frac{\text{b}}{\sin \angle \text{B}}=2\text{R}\) и\( \large\displaystyle \frac{\text{c}}{\sin \angle \text{C}}=2\text{R}\).
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол.
И всё!
Расположение центра описанной окружности
А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника.
Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.
И вообще:
В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника.

В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника.

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 6. Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.
Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
ЕГЭ 6. Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие свойства.
В какие фигуры можно, а в какие нельзя вписать окружность. Научимся решать задачи на вписанную окружность.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
ElPrg
29 октября 2019
Очень полноценно! Спасибо!
Александр (админ)
29 октября 2019
Спасибо и вам, ElPrg (что бы это имя ни значило 🙂
Ольга
28 ноября 2019
Спасибо! Очень понятно и доходчиво изложили материал. Есть еще на свете смысловики!!!
Александр (админ)
28 ноября 2019
Как хорошо вы нас называли! «Смысловики!». Спасибо.
Александр
19 декабря 2019
Доступно и понятно! Спасибо автору!
Александр (админ)
19 декабря 2019
Спасибо, тезка!