Теорема синусов
Привет!
Существуют две теоремы, свзанные с тригонометрией, которые могут оказать тебе огромную услугу в решении задач — теорема синусов и теорема косинусов.
Особенно в решении задач продвинутого уровня, за которые можно получит неплохие баллы на экзамене!
О теореме косинусов можешь прочитать пройдя по ссылке, а здесь мы поговорим про теорему синусов. Легкую и полезную.
Поехали!
Теорема синусов — коротко о главном
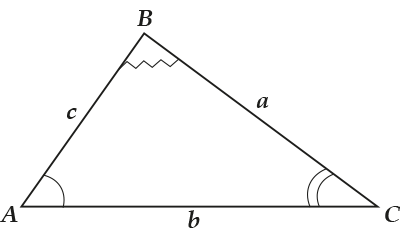
Для любого \( \displaystyle \Delta ABC\):
\( \displaystyle \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\)
(здесь \( \displaystyle R\) – радиус описанной окружности)
Теорема синусов — подробнее
Что же нам сообщает теорема синусов? Вероятнее всего, что-нибудь о синусах, не правда ли? Давай сформулируем.
Для любого \( \displaystyle \Delta ABC\)\( \displaystyle \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\)(здесь \( \displaystyle R\) – радиус описанной окружности).

Первый вопрос, который возникает при взгляде на эту формулу: «Но при чём же здесь вообще \( \displaystyle R\)?».
Вот давай именно с него и начнём.
Теорема синусов. Доказательство
Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр \( \displaystyle BO\).
Пусть этот диаметр пересекает окружность в точке \( \displaystyle K\). Давай рассмотрим \( \displaystyle \Delta BKC\).
Что же это за треугольник?
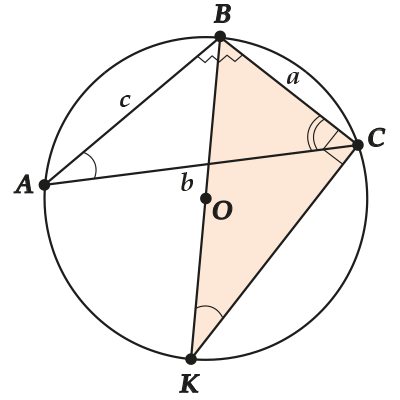
Ну, конечно же, прямоугольный, ведь в \( \displaystyle \Delta BKC\) угол \( \displaystyle C\) опирается на диаметр \( \displaystyle BK\quad\Rightarrow \quad\angle C=90{}^\circ \) (вспоминаем тему «Вписанный и центральный угол окружности»).
Но и кроме того, \( \displaystyle \angle K\) в \( \displaystyle \Delta BKC\) равен \( \displaystyle \angle A\) в \( \displaystyle \Delta ABC\), потому что эти углы опираются на одну дугу \( \displaystyle BC\) (опять вспоминаем ту же тему).
А теперь просто запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta BKC\) \( \displaystyle \sin \angle K=\frac{a}{BK}\).
Но ведь \( \displaystyle BK\) – диаметр \( \displaystyle \quad\Rightarrow\quad BK=2R\), и \( \displaystyle \sin \angle K=\frac{a}{2R}\).
Вспомним, что \( \displaystyle \angle K=\angle A\) и получим \( \displaystyle \sin \angle A=\frac{a}{2R}\quad\Rightarrow\quad \frac{a}{\sin \angle A}=2R\).
Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.
Но как же быть с углами \( \displaystyle B\) и \( \displaystyle C\)? – спросишь ты.
Да, точно также. Давай рассмотрим \( \displaystyle \angle B\).
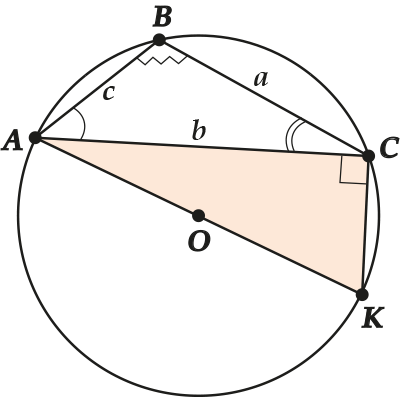
Теперь проведём диаметр \( \displaystyle AO\) и соединим точки \( \displaystyle K\) и \( \displaystyle C\).
Как-то тут немного по-другому получается, ты заметил? \( \displaystyle \Delta AKC\), конечно, прямоугольный, так как \( \displaystyle \angle C\) опирается на диаметр \( \displaystyle AK\).
Но теперь \( \displaystyle \angle K+\angle B=180{}^\circ \), потому что четырехугольник \( \displaystyle ABCK\) – вписанный. (Надеюсь, ты ещё помнишь, что для угла \( \displaystyle A\) у нас было \( \displaystyle \angle A=\angle K\).) В чём же дело?
Ну, просто \( \displaystyle \angle B\) – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся.
Итак, запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta AKC\).
\( \displaystyle \sin \angle K=\frac{b}{AK}\); то есть \( \displaystyle \sin \angle K=\frac{b}{2R}\)
Но \( \displaystyle \angle B=180{}^\circ -\angle K\Rightarrow \sin \angle B=\sin \angle K\) (читаем или вспоминаем формулы приведения в тригонометрии.)
Значит, \( \displaystyle \sin \angle B=\frac{b}{2R}\quad\Rightarrow\quad \frac{b}{\sin \angle B}=2R\).
Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле \( \displaystyle C\), то проделай все те же действия самостоятельно и убедись, что все получается.
Обрати внимание, что мы доказали «четверное равенство».
\( \displaystyle \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\)в такой последовательности:
\( \displaystyle \left\{ \begin{array}{l}\frac{a}{\sin \angle A}=2R\\\frac{b}{\sin \angle B}=2R\hspace{13mm}\Rightarrow\quad \frac{a}{\sin \angle A}=\frac{b}{\sin \angle B}=\frac{c}{\sin \angle C}=2R\\\frac{c}{\sin \angle C}=2R\end{array} \right.\)А теперь внимание! Обсудим пользу этой теоремы
Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.
Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует \( \displaystyle R\)?! Возможно, правда, ты знаком с формулой \( \displaystyle S=\frac{abc}{4R}\), то есть \( \displaystyle R=\frac{abc}{4S}\quad\), но!
Давай – ка сравним:
Из теоремы синусов: \( \displaystyle R=\frac{a}{2\sin \angle A}\)
Из формулы площади: \( \displaystyle R=\frac{abc}{4S}\).
Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить?
А кроме того, открою тебе маленький секрет: формула \( \displaystyle S=\frac{abc}{4R}\) как раз и доказывается именно с применением теоремы синусов.
Чтобы убедиться в этом, читай темы «Площадь круга», «Площадь треугольника и четырехугольника».
Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол.
Но в основном теорема синусов – главный инструмент для нахождения радиуса описанной окружности.
Запомни это очень хорошо!
Бонус: Вебинар из нашего курса подготовки к ЕГЭ
ЕГЭ 6, 14, 16. Теорема косинусов и синусов
Универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


