Объем призмы и другие ее характеристики
Перед вами иллюстрированный гид о призме.
В картинках. С пояснениями к формулам. С примерами.
Определение, виды призм, высота, площадь, объем призмы — все, все, все!
Читайте и делитесь впечатлениями в комментариях!
Призма — коротко о главном
Определение призмы:
Призма – это многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а боковые грани – параллелограммы.
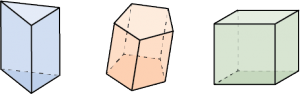
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
Виды призм:
Параллелепипед — это призма, основанием которой является параллелограмм.
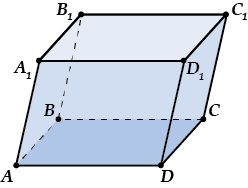
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.
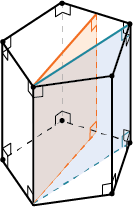
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы – равные прямоугольники.
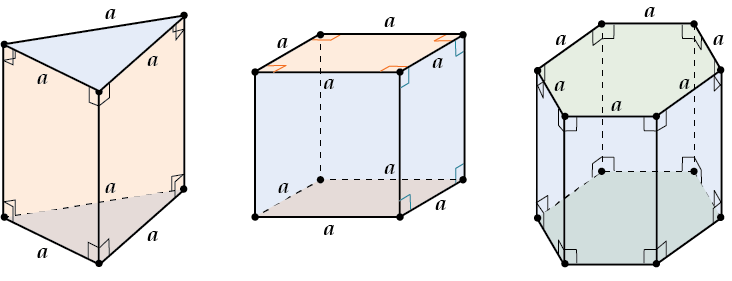
Объем призмы
Главная формула объема призмы:
\( \displaystyle V=S{{\ }_{основания}}\cdot \text{H}\),
где \( {{\text{S}}_{основания}}\) – площадь основания,
\( H\) – высота.
Необычная формула объема призмы:
\( \text{V}={{\text{S}}_{\bot }}\cdot l\),
где \( {{\text{S}}_{\bot }}\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра.
Площадь призмы
Площадь полной поверхности призмы – сумма площадей всех граней.
\( \displaystyle {{\text{S}}_{полн. пов.}}={{\text{S}}_{боков.пов.}}+2\cdot {{\text{S}}_{\text{основания}.}}\)
А теперь чуть подробнее…
Для справки: по планиметрии и стереометрии в нашем учебнике для подготовки к ЕГЭ есть все темы. Например: пирамида (ЕГЭ №14), трапеция, прямоугольный треугольник.
Заходите и готовьтесь к ЕГЭ.
Что такое призма
Давай ответим сперва картинками:

Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями.
Остальные грани называются боковыми.
Плоскости оснований параллельный. Боковые грани – параллелограммы.
Рисуем еще раз.
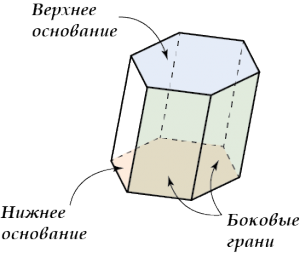
А теперь рёбра.
Смотри: бывают рёбра основания и боковые рёбра.
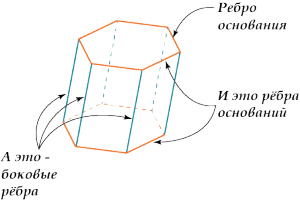
Важно знать, что:
Все боковые рёбра призмы равны и параллельны.
А еще:
- Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то четырёхугольной и т.д.;
- Бывают и десятиугольные, и двадцатиугольные призмы, но, к счастью, не в твоих задачах;
- А тебе будут встречаться чаще всего треугольные, четырёхугольные и шестиугольные призмы.
Думаю, теперь мы можем дать более строгое определение призмы.
Определение призмы
Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.
Виды призм
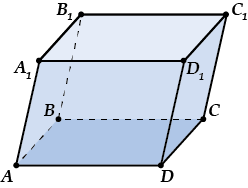
Призма, основанием которой является параллелограмм, называется параллелепипедом.
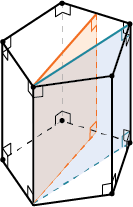
Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания.
Другие призмы называются наклонными.
Высота призмы
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
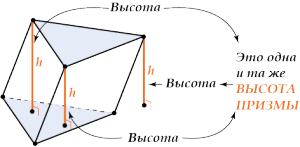
И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.
Согласен?
Объем призмы
Главная формула объема призмы
\( \displaystyle V=S{{\ }_{основания}}\cdot \text{H}\),где \( {{\text{S}}_{основания}}\) — площадь основания,
\( H\) — высота.
Необычная формула объема призмы
\( \text{V}={{\text{S}}_{\bot }}\cdot l\),
где \( {{\text{S}}_{\bot }}\) — площадь сечения, перпендикулярного боковому ребру,
\( l\) — длина бокового ребра.
Площадь призмы
Площадь полной поверхности призмы – сумма площадей всех граней.
\( \displaystyle {{\text{S}}_{полн. пов.}}={{\text{S}}_{боков.пов.}}+2\cdot {{\text{S}}_{\text{основания}.}}\)
Прямая призма
Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
Свойства прямой призмы:
- Все боковые грани прямоугольники;
- Все сечения, проходящие через боковые рёбра, – прямоугольники;
- Даже сечения, проходящие только через одно боковое ребро, – прямоугольники;
- У прямой призмы высота совпадает с боковым ребром.

Правильная призма
Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.
То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Тебе, скорее всего, может встретиться:
Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.
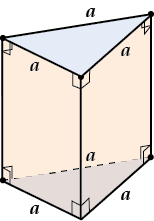
Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.
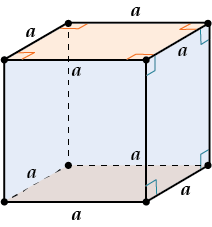
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
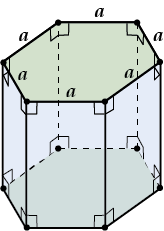
Главная формула объема призмы
\( \displaystyle V=S{{\ }_{основания}}\cdot \text{H}\)\( {{\text{S}}_{основания}}\) – площадь основания
\( H\) – высота
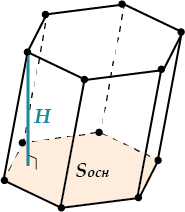
Эта формула верна для любой призмы, но если призма прямая, то \( H\) «превращается» в боковое ребро. И тогда
\( \displaystyle V=S{{\ }_{основания}}\cdot \text{H}\)– то же самое, что
\( \displaystyle V=S{{\ }_{основания}}\cdot боковое\ ребро\)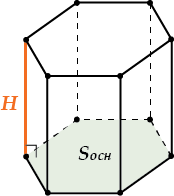
Необычная формула объёма призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы:
\( \Large \text{V}={{\text{S}}_{\bot }}\cdot l\)\( {{\text{S}}_{\bot }}\) – площадь сечения, перпендикулярного боковому ребру,
\( l\) – длина бокового ребра
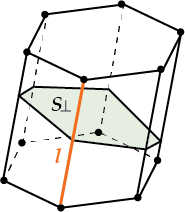
Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Давай теперь для упражнения посчитаем объём самых популярных призм.
Объем правильной треугольной призмы
Пусть дано, что сторона основания равна \( a\), а боковое ребро равно \( b\).
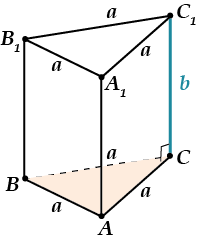
Найдем объем:
\( \text{V}={{\text{S}}_{Основания}}\cdot \text{H}={{\text{S}}_{\text{ABC}}}\cdot \text{b}\)
Вспомним, как находить площадь правильного треугольника:
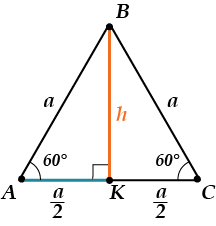
Подставляем в формулу объёма:
\( \text{V}={{\text{S}}_{\text{ABC}}}\cdot \text{b}=\frac{{{\text{a}}^{2}}\text{b}\sqrt{3}}{4}\).
Объем правильной четырёхугольной призмы
Опять дано: сторона основания равна \( a\), боковое ребро равно \( b\).
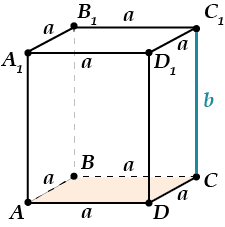
\( \text{V}={{\text{S}}_{\text{основания}}}\cdot \text{H}={{\text{S}}_{\text{ABC}}}\cdot \text{b}\)
Ну, площадь квадрата долго искать не надо:
\( \displaystyle {{\text{S}}_{\text{ABCD}}}={{\text{a}}^{2}}\)Значит, \( \displaystyle \text{V}={{\text{S}}_{\text{ABCD}}}\cdot \text{b}={{\text{a}}^{2}}\text{b}\).
Объем правильной шестиугольной призмы
Площадь поверхности призмы
Площадь боковой поверхности призмы – сумма площадей всех боковых граней.
Есть ли общая формула?
Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.
Площадь полной поверхности призмы – сумма площадей всех граней.
\( \displaystyle {{\text{S}}_{полн. пов.}}={{\text{S}}_{боков.пов.}}+2\cdot {{\text{S}}_{\text{основания}.}}\)
Формулу можно написать для прямой призмы:
\( \displaystyle {{\text{S}}_{боков.}}=\text{H}\cdot \text{P}\), где \( \displaystyle P\) – периметр основания.
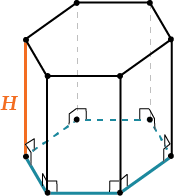
\( \displaystyle {{\text{S}}_{\text{полной}}}=\text{H}\cdot \text{P}+2{{\text{S}}_{основания}}\).
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.
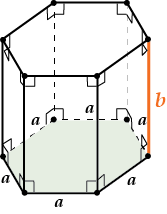
Для примера посчитаем полную поверхность правильной шестиугольной призмы
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Шикарный сайт, шикарное объяснение, без воды, спасибо вам большое👍
Спасибо за шикарный отзыв! )
Тут всё понятно,впервые начинаю понимать стереометрию
Супер Aper! Рады помочь!
Когда читаю теорию этого учебника, такое ощущение, что я разговариваю с другом. Настолько все просто и приятно. Сказать, что я влюбилась в этот материал, ничего не сказать. Спасибо вам!
Бася, вы нас растрогали таким комментарием. Спасибо большое! Удачи на экзамене!
Некоторые комментарии прошлых лет об этой статье:
Илья
26 ноября 2017
Огромное вам спасибо за созданный сайт, он очень удобен и информативен. Мне сложно представить какое количество времени было потрачено на «переработку» материала в понятном и доступном виде.Теперь есть источник чистых знаний, без лишней «воды», который не только помогает узнать новое, но и систематизировать информацию в голове. Жаль, что я не нашел сайт раньше. Вы лучшие!
Дмитрий
21 февраля 2018
Сайт отличный!Все подробно описано. Никогда не понимал эту тему, но благодаря создателям этого сайта я наконец понял эту тему. Спасибо вам за ваши труды!!! Очень вам благодарен.
Regina
29 марта 2018
Аааааааа,это просто лучшее. Никогда не разбиралась в геометрии…Готовясь к зачету искала все сайты на эту тему. Нашла вас. Ввы все объяснили просто и доступно. Спасибо большое!
Настя
21 мая 2018
Красивый сайт, ничего глаза не режет, смотреть и читать приятно.
Женя
27 февраля 2019
можете указать свои инициалы? мне это для проекта надо)
Анна
29 апреля 2019
Преподнесено очень понятным языком, с наглядными картинками, спасибо) Хотелось бы хоть пример одной задачи и решение чтобы было открыто бесплатно, чтобы понять на сколько хорошо поясняете, но я думаю все ок.
Жанна
27 апреля 2020
Спасибо! Я — учитель и мне очень понравилось!
Николай
04 июня 2020
Все очень доступно и понятно. Только вот не написано в статье про диагональ призмы. А так все просто супер, подготовился к сессии по данному материалу 🙂
Алексей Шевчук
05 июня 2020
Николай, спасибо. Диагонали в разных призмах разные, а в треугольной её и вовсе нет, поэтому длина диагонали — частный случай, а не какая-то полезная формула. Стоит рассмотрения разве что диагональ прямоугольного параллелепипеда — она вычисляется по теореме Пифагора и равна корню из суммы квадратов рёбер.