Объем пирамиды
В этой статье вы поймете что такое пирамида и какими они бывают.
Вы научитесь вычислять объем пирамиды, высоту и другие ее параметры.
Вы научитесь решать задачу на доказательство (ЕГЭ №14) и записывать доказательства так, чтобы не сняли баллы на ЕГЭ.
Приступим?
Объем пирамиды — коротко о главном
Определение пирамиды:
Пирамида – это многогранник, который состоит из любого плоского многоугольника (основание пирамиды), точки, не лежащей в плоскости основания, (вершина пирамиды) и всех отрезков, соединяющих вершину пирамиды с точками основания.
Треугольники, в которые «сливаются» эти отрезки, называются боковыми гранями, а отрезки, проведённые к вершинам основания — это боковые ребра.
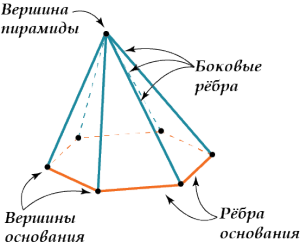
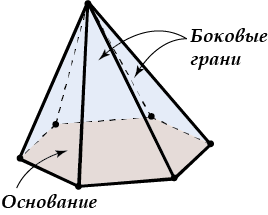
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Правильная пирамида — пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.
Свойства правильной пирамиды:
- В правильной пирамиде все боковые рёбра равны.
- Все боковые грани – равнобедренные треугольники и все эти треугольники равны.
Объем пирамиды:
\( \displaystyle V=\frac{1}{3}{{S}_{osn}}\cdot H\)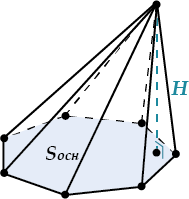
Что такое пирамида
Как она выглядит?
Вместо того, чтобы читать длинное определение, достаточно просто посмотреть на картинку:
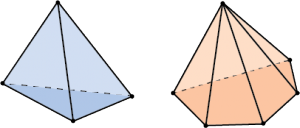
Видишь: у пирамиды внизу (говорят «в основании») какой-нибудь многоугольник, и все вершины этого многоугольника соединены с некоторой точкой в пространстве (эта точка называется «вершина»).
У всей этой конструкции ещё есть боковые грани, боковые рёбра и рёбра основания.
Ещё раз нарисуем пирамиду вместе со всеми этими названиями:


Некоторые пирамиды могут выглядеть очень странно, но всё равно это – пирамиды.
Вот, например, совсем «косая» пирамида.
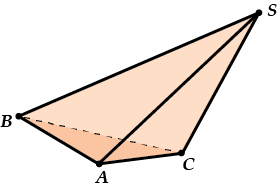
И ещё немного о названиях: если в основании пирамиды лежит треугольник, то пирамида называется треугольной, если четырёхугольник, то четырёхугольной, а если стоугольник, то … догадайся сам.
Высота пирамиды
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
При этом точка, куда oпустилась высота, называется основанием высоты.

Обрати внимание, что в «кривых» пирамидах высота может вообще оказаться вне пирамиды.
Вот так:
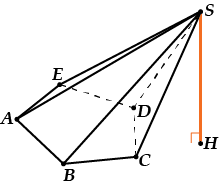
И ничего в этом страшного нет. Похоже на тупоугольный треугольник.
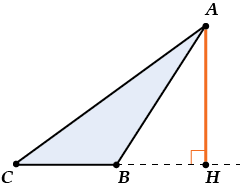
Правильная пирамида
Правильной называется такая пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.
Много сложный слов?
Давай расшифруем: «В основании – правильный многоугольник» — это понятно.
А теперь вспомним, что у правильного многоугольника есть центр – точка, являющаяся центром и вписанной, и описанной окружности.
Ну вот, а слова «вершина проецируется в центр основания» означают, что основание высоты попадает как раз в центр основания. Смотри, как ровненько и симпатично выглядит правильная пирамида.
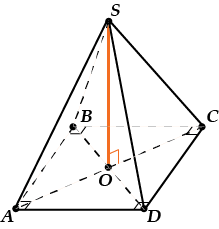
Четырехугольная правильная пирамида
В основании – квадрат, вершина \( \displaystyle S\) проецируется в точку пересечения диагоналей этого квадрата.
Треугольная правильная пирамида
В основании – правильный треугольник, вершина \( \displaystyle S\) проецируется в точку пересечения высот (они же и медианы, и биссектрисы) этого треугольника.

Очень важные свойства правильной пирамиды
В правильной пирамиде:
- Все боковые ребра равны
- Все боковые грани – равнобедренные треугольники и все эти треугольники равны.
Объем пирамиды
Главная формула объема пирамиды
\( \displaystyle \Large V=\frac{1}{3}{{S}_{осн}}\cdot H\)

Откуда взялась именно \( \displaystyle \frac{1}{3}\)?
Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac{1}{3}\), а у цилиндра – нет.
Теперь давай посчитаем объем самых популярных пирамид.
Объем правильной треугольной пирамиды
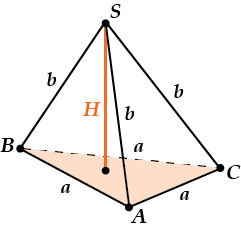
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle H\).
\( \displaystyle {{S}_{осн}}\) – это площадь правильного треугольника \( \displaystyle ABC\).
Вспомним, как искать эту площадь.
Используем формулу площади:
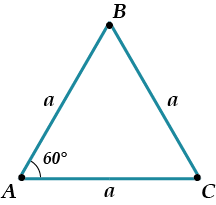
\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \)
У нас «\( \displaystyle a\)» – это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60{}^\circ =\frac{\sqrt{3}}{2}\)
Значит, \( \displaystyle {{S}_{ABC}}=\frac{1}{2}{{a}^{2}}\frac{\sqrt{3}}{2}=\frac{{{a}^{2}}\sqrt{3}}{4}\).
Теперь найдем \( \displaystyle H\).
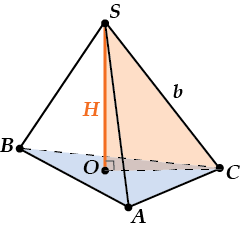
По теореме Пифагора для \( \displaystyle \Delta SOC\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}\)
Чему же равно \( \displaystyle OC\)?
Это радиус описанной окружности в \( \displaystyle \Delta ABC\), потому что пирамида правильная и, значит, \( \displaystyle O\) — центр \( \displaystyle \Delta ABC\)
Найдем \( \displaystyle OC\) (Подробнее смотри в теме «Правильный треугольник»).
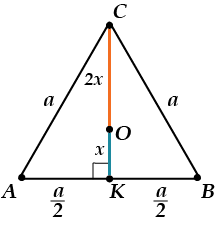
\( \displaystyle OC=\frac{2}{3}CK\), так как \( \displaystyle O\) — точка пересечения и медиан тоже.
\( \displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}\) (теорема Пифагора для \( \displaystyle \Delta ACK\))
\( \displaystyle C{{K}^{2}}-{{a}^{2}}-\frac{{{a}^{2}}}{4}=\frac{3{{a}^{2}}}{4}\); \( \displaystyle CK=\frac{a\sqrt{3}}{2}\)
Значит, \( \displaystyle OC=\frac{2}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)
Подставим \( \displaystyle OC\) в формулу для \( \displaystyle H\).
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}={{b}^{2}}-\frac{{{a}^{2}}}{3}\)
И подставим все в формулу объема:
\( \displaystyle V=\frac{1}{3}{{S}_{ABC}}\cdot H=\frac{1}{3}\cdot \frac{{{a}^{2}}\sqrt{3}}{4}\cdot \sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}\)
\( \displaystyle V=\frac{{{a}^{2}}\sqrt{3}}{12}\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{3}}\).
Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:
\( \displaystyle V=\frac{{{a}^{3}}}{6\sqrt{2}}\).
Объем правильной четырехугольной пирамиды
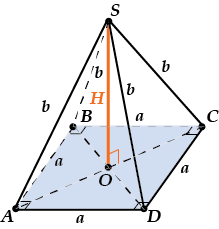
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}H\).
Здесь \( \displaystyle {{S}_{OCH}}\) и искать не нужно; ведь в основании – квадрат, и поэтому \( \displaystyle {{S}_{OCH}}={{a}^{2}}\).
Найдем \( \displaystyle H\). По теореме Пифагора для \( \displaystyle \Delta SOD\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-O{{D}^{2}}\)
Известно ли нам \( \displaystyle OD\)? Ну, почти. Смотри:
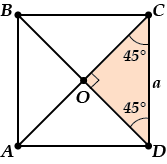
\( \displaystyle OD=a\cdot \cos 45{}^\circ =\frac{a}{\sqrt{2}}\) (это мы увидели, рассмотрев \( \displaystyle \Delta COD\))
Подставляем \( \displaystyle OD\) в формулу для \( \displaystyle H\):
\( \displaystyle {{H}^{2}}={{b}^{2}}-\frac{{{a}^{2}}}{2}\)
\( \displaystyle H=\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{2}}\)
А теперь и \( \displaystyle H\) и \( \displaystyle {{S}_{OCH}}\) подставляем в формулу объема.
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}\cdot H=\frac{1}{3}{{a}^{2}}\sqrt{{{b}^{2}}-\frac{{{a}^{2}}}{2}}\).
Объем правильной шестиугольной пирамиды
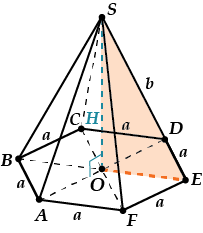
Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).
\( \displaystyle V=\frac{1}{3}{{S}_{OCH}}\cdot H\)
Как найти \( \displaystyle {{S}_{OCH}}\)? Смотри, шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете объема правильной треугольной пирамиды, здесь используем найденную формулу.
\( \displaystyle {{S}_{ABCDEF}}=6\cdot {{S}_{AOF}}=6\cdot \frac{{{a}^{2}}\sqrt{3}}{4}=\frac{3\sqrt{3}{{a}^{2}}}{2}\)
Теперь найдем \( \displaystyle H\) (это \( \displaystyle SO\)).
По теореме Пифагора для \( \displaystyle \Delta SOE\)
\( \displaystyle {{H}^{2}}={{b}^{2}}-OE\)?
Но чему же равно \( \displaystyle OE\)? Это просто \( \displaystyle a\), потому что \( \displaystyle \Delta EOF\) (и все остальные тоже) правильный.
Значит,
\( \displaystyle {{H}^{2}}={{b}^{2}}-{{a}^{2}}\)
\( \displaystyle H=\sqrt{{{b}^{2}}-{{a}^{2}}}\)
Подставляем:
\( \displaystyle V=\frac{1}{3}{{S}_{OSN}}\cdot H=\frac{1}{3}\cdot \frac{3\sqrt{3}{{a}^{2}}}{2}\cdot \sqrt{{{b}^{2}}-{{a}^{2}}}\)
\(\displaystyle V=\frac{\sqrt{3}}{2}{{a}^{2}}\sqrt{{{b}^{2}}-{{a}^{2}}}\)
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020
В этом видео мы разобрали следующие вопросы:
- Как нарисовать шестиугольную пирамиду и как исправить рисунок, если грани пирамиды сливаются.
- Как правильно подписать вершины пирамиды.
- Как доказать пункты А и Б задания №14 из ЕГЭ и записать доказательство так, чтобы не сняли баллы на экзамене.
- Как найти площадь основания пирамиды (чтобы найти объем) и правильно записать решение.
- Как найти объем пирамиды.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



«Катастрофа»
Спасибо! Кратко, доступно. Для повторения перед экзаменом , что называется «освежить в памяти основное» на отлично
Спасибо, Татьяна!