Решение тригонометрических уравнений — 39 примеров!
Привет!
Сегодня мы с тобой изучим, как решать одну из разновидностей уравнений – тригонометрические. Мы решим 39(!) примеров, от самых простых, до самых сложных.
И станем на шаг ближе к заветной цели – сдать ЕГЭ по математике так, чтобы поступить в ВУЗ мечты!
Поехали!
Тригонометрические уравнения — коротко о главном
Тригонометрическое уравнение – это уравнение, в котором неизвестная находится строго под знаком тригонометрической функции.
Существует два способа решения тригонометрических уравнений:
Первый способ – с использованием формул.
Второй способ – через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.
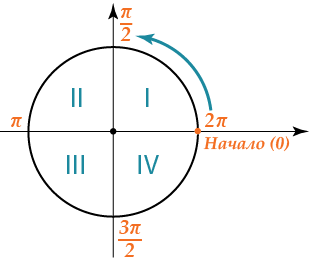
Чтобы уметь решать тригонометрические уравнения необходимо знать как минимум следующее:
- что такое синус, косинус, тангенс, котангенс;
- какие знаки принимает та или иная тригонометрическая функция в разных четвертях тригонометрической окружности;
- какие из этих функций нечётные, а какие – чётные;
- знание значений тригонометрических функций в основных углах 1 четверти.
Если ты что-то не знаешь, повтори следующие разделы:
- Синус, косинус, тангенс и котангенс угла и числа
- Тригонометрическая окружность
- Формулы тригонометрии
Этого будет вполне достаточно. Если это по ходу моего повествования окажется не так, то не сердись, придётся вспомнить что-нибудь ещё, не упомянутое здесь.
Простейшие тригонометрические уравнения
Что же это такое, как ты думаешь? Является ли, например, уравнение
\( \displaystyle \frac{2}{2{x}-11}=\frac{1}{3}\)
тригонометрическим?
Ты и сам прекрасно понимаешь, что нет! Потому что ни одной тригонометрической функции \( \displaystyle \left( sin x,cos x,tg x,ctg x \right)\) в нём и в помине нет!
А что насчёт вот такого уравнения?
\( \displaystyle sin2x+3x=2\)
И опять ответ отрицательный!
Это так называемое уравнение смешанного типа.
Оно содержит как тригонометрическую составляющую, так и линейную (\( \displaystyle 3x\)).
Некоторые типы подобных уравнений мы будем с тобой решать в следующих раздела этой статьи.
Но вернёмся к вопросу: «Что же такое тригонометрические уравнения?»
Тригонометрические уравнения –это уравнения, в которых неизвестная находится строго под знаком тригонометрической функции!
Например:
- \( \displaystyle 6co{{s}^{2}}x+5sin{x}-7=0\)
- \( \displaystyle sin\pi \sqrt{x}=-1\)
- \( \displaystyle \frac{3}{5}sinx+\frac{4}{5}cosx=1\) и т.д.
Однако для начала мы не будем решать сложные и иногда неприступные тригонометрические уравнения, а ограничимся самыми простыми уравнениями вида:
- \( \displaystyle sinf\left( x \right)=a\)
- \( \displaystyle cosf\left( x \right)=a\)
- \( \displaystyle tgf\left( x \right)=a\)
- \( \displaystyle ctgf\left( x \right)=a\)
Где \( \displaystyle a\) – некоторое постоянное число.
Например: \( \displaystyle 0,5;~1;~-1;\pi ;\ ~1-\sqrt{3};~1000\) и т. д.
\( \displaystyle f\left( x \right)\) – некоторая функция, зависящая от искомой переменной \( \displaystyle x\), например \( \displaystyle f\left( x \right)=x,~f\left( x \right)=2-x,~f\left( x \right)=\frac{\pi x}{7}\) и т. д.
Такие уравнения называются простейшими!
Основная цель решения ЛЮБОГО тригонометрического уравнения – это свести его к виду простейшего!
Для этого, как правило, используют аппарат, который я описал в разделе «Формулы тригонометрии«
Так что очень важно, я бы даже сказал, жизненно необходимо научиться решать простейшие уравнения, ибо они – фундамент для решения сложных примеров.
Как часто тригонометрические уравнения встречаются на ЕГЭ?
Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:
- Задача №5 (простейшее тригонометрическое уравнение – встречается время от времени);
- Задача №10 (задача с прикладным содержанием, которая включает в себя решение тригонометрического уравнения – встречается изредка);
- Задача №12 (она на производную, но в конечном счёте сводится к решению простейшего тригонометрического уравнения – ЧАСТО ВСТРЕЧАЕТСЯ В ЕГЭ)
- Задача №13 – даёт 2 первичных балла – (решение тригонометрического уравнения средней или высокой сложности – ОЧЕНЬ ЧАСТО, ПРАКТИЧЕСКИ ВСЕГДА!)
Так что, как ты понимаешь, при некоторых раскладах, навык решения данного вида уравнений может добавить в твою копилку аж 5 первичных баллов из 32!
Два способа решения тригонометрических уравнений – через формулы и по кругу
В принципе, я не могу сказать, что легче: держать в голове, как строится круг, или помнить 4 формулы.
Тут решать тебе самому, однако я всё же предпочитаю решать данные уравнения через формулы, поэтому здесь я буду описывать именно этот метод.
Вначале мы начнём с «самых простейших» из простейших уравнений вида:
- \( \displaystyle \text{sinx}=\text{a}\),
- \( \displaystyle \text{cosx}=\text{a}\),
- \( \displaystyle \text{tgx}=\text{a}\),
- \( \displaystyle \text{ctgx}=\text{a}\).
Я хочу сразу оговориться вот о чем, будь внимателен:
Уравнения вида: \( \displaystyle sinf\left( x \right)=a\), \( \displaystyle cosf\left( x \right)=a\) имеют смысл только тогда, когда \( \displaystyle -1\le \text{a}\le 1\)
Уравнения вида: \( \displaystyle \text{tgx}=\text{a}\), \( \displaystyle \text{ctgx}=\text{a}\) имеют смысл уже при всех значениях \( \displaystyle \text{a}\).
То есть, тебе не надо знать вообще никаких формул, чтобы спокойно ответить, что уравнения, например:
\( \displaystyle sinx=1000\)
\( \displaystyle cos\left( 3{x}-sin\left( x \right) \right)=2\)
\( \displaystyle sin\left( 2{{x}^{2}}-2x+1 \right)=-3\)
Корней не имеют!!!
Почему?
Потому что они «не попадают» в промежуток от минус единицы до плюс единицы.
Ещё раз скажу: внимательно обдумай эти слова, они уберегут тебя от многих глупых ошибок!!!
Для остальных же случаев тригонометрические формулы такие как в этой таблице.
| \( \displaystyle A\) | \( \displaystyle a\) | \( \displaystyle -1\) | \( \displaystyle 0\) | \( \displaystyle 1\) |
|---|---|---|---|---|
| \( \displaystyle \sin x=A\) | \( \displaystyle {{\left( -1 \right)}^{n}}\arcsin \alpha +\pi n\) | \( \displaystyle -\frac{\pi }{2}+2\pi n\) | \( \displaystyle \pi n\) | \( \displaystyle \frac{\pi }{2}+2\pi n\) |
| \( \displaystyle \cos x=A\) | \( \displaystyle \pm \arccos \alpha +2\pi n\) | \( \displaystyle \pi +2\pi n\) | \( \displaystyle \frac{\pi }{2}+\pi n\) | \( \displaystyle 2\pi n\) |
| \( \displaystyle tgx=A\) | \( \displaystyle arctg\alpha +\pi n\) | \( \displaystyle -\frac{\pi }{4}+\pi n\) | \( \displaystyle \pi n\) | \( \displaystyle \frac{\pi }{4}+\pi n\) |
| \( \displaystyle ctgx=A\) | \( \displaystyle arcctg\alpha +\pi n\) | \( \displaystyle \frac{3\pi }{4}+\pi n\) | \( \displaystyle \frac{\pi }{2}+\pi n\) | \( \displaystyle \frac{\pi }{4}+\pi n\) |
На самом деле в этой таблице данных немного больше, чем нужно.
Тебе нужно лишь запомнить первые два её столбца, другие столбцы – частные случаи решения тригонометрических уравнений.
Я, допустим, никогда не утруждаю себя их запоминанием, а вывожу ответ из основных формул.
Глядя на таблицу, не возникло ли у тебя пары вопросов?
У меня бы возникли вот какие:
Что такое \( \displaystyle n\) и что такое, например \( \displaystyle arcsin\alpha ~\left( arccos\alpha ,~arctg\alpha ,~arcctg\alpha \right)\)?
Отвечаю на все по порядку:
\( \displaystyle n\) – это любое целое число \( \displaystyle \left( 0,\text{ }1,\text{ }-1,\text{ }2,\text{ }-2,\text{ }\ldots .\text{ } \right)\).
В чем уникальная особенность тригонометрических уравнений перед всеми остальными, которые ты изучал?
ОНИ ИМЕЮТ БЕСКОНЕЧНОЕ КОЛИЧЕСТВО КОРНЕЙ!!!
И число \( \displaystyle n\) и служит для обозначения этой «бесконечности».
Конечно, вместо \( \displaystyle n\) можно писать любую другую букву, только не забывай добавить в ответе: \( \displaystyle n\in Z\) – что означает, что \( \displaystyle n\) – есть любое целое число.
Теперь насчёт арксинуса и других «арок». Вообще, так записываются обратные тригонометрические функции и понимать, скажем, \( \displaystyle arcsin\alpha \) надо как «угол, синус которого равен \( \displaystyle \alpha \)«
- \( \displaystyle arcsin\alpha\)– угол, синус которого равен \( \displaystyle \alpha\)
- \( \displaystyle arccos\alpha\)– угол, косинус которого равен \( \displaystyle \alpha\)
- \( \displaystyle \alpha\)\( \displaystyle arctg\alpha\)– угол, тангенс которого равен \( \displaystyle \alpha\)
- \( \displaystyle \alpha\)\( \displaystyle arcctg\alpha\) – угол, котангенс которого равен \( \displaystyle \alpha\)
Например,
- \( \displaystyle \arcsin \left( 0 \right)=0,\)
- \( \displaystyle \arccos \left( \frac{\sqrt{2}}{2} \right)=\frac{\pi }{4},\)
- \( \displaystyle \ arctg\left( 1 \right)=\frac{\pi }{4},\)
- \( \displaystyle \arcsin \left( 0,5 \right)=\frac{\pi }{6},\)
- \( \displaystyle \arccos \left( \frac{\sqrt{3}}{2} \right)=\frac{\pi }{6},\)
- \( \displaystyle \ arctg\left( \sqrt{3} \right)=\frac{\pi }{3}\)
то есть,
Алгоритм вычисления арксинусов и других «арок»
- Смотрим на то, что стоит под «аркой» – какое там число
- Смотрим, какая у нас «арка» – для синуса ли, или для косинуса, тангенса или котангенса
- Смотрим, чему равен угол (1 четверти), для которого синус, косинус, тангенс, котангенс равен числу, стоящему под аркой
- Записываем ответ
Вот простой пример вычисления аркосинуса:
\( \displaystyle \arccos \left( \frac{\sqrt{3}}{2} \right)\)Решение:
- Под аркой число \( \displaystyle \frac{\sqrt{3}}{2}\)
- Арка для функции – косинус!
- Косинус какого угла равен \( \displaystyle \frac{\sqrt{3}}{2}\)? Угла \( \displaystyle \frac{\pi }{6}\) (или \( \displaystyle 30\) градусов!)
- Тогда \( \displaystyle \arccos \left( \frac{\sqrt{3}}{2} \right)=\frac{\pi }{6}\)
Сам посчитай:
- \( \displaystyle \ arctg\left( \frac{1}{\sqrt{3}} \right)\)
- \( \displaystyle \arcsin \left( \frac{\sqrt{3}}{2} \right)\)
Ответы:
\( \displaystyle \frac{\pi }{6}\) и \( \displaystyle \frac{\pi }{3}\).
Если «арка» берется от отрицательного числа?
Всё ли я сказал про «арки»? Почти что да! Остался вот какой момент.
Что делать, если «арка» берётся от отрицательного числа?
Лезть в таблицу – как бы не так! Для арок выполняются следующие формулы:
- \( \displaystyle \text{arcsin}\left( -\alpha \right)=-\text{arcsin}\alpha \)
- \( \displaystyle \text{arctg}\left( -\alpha \right)=-\text{arctg}\alpha \)
И внимание!!!
- \( \displaystyle \text{arcctg}\left( -\alpha \right)=\text{ }\!\!\pi\!\!\text{ }-\text{arcctg}\alpha \)
- \( \displaystyle \text{arccos}\left( -\alpha \right)=\text{ }\!\!\pi\!\!\text{ }-\text{arccos}\alpha \)
Чтобы запомнить, ориентируемся на обычные тригонометрические функции: грубо говоря, синус и тангенс мы смотрим на тригонометрической окружности по вертикальной оси, а косинус и котангенс – по горизонтальной.
Соответственно, для арксинуса и арктангенса выбираем две четверти по вертикали: первую и четвёртую (минусик выносится из аргумента и ставится перед функцией), а для арккосинуса и арккотангенса – по горизонтали: первую и вторую.
В первой и второй четвертях аргумент уже не может быть отрицательным, поэтому и получаются формулы не совсем похожими.
Ну всё, теперь мы можем приступать к решению простейших уравнений!
Решение 11-ти простейших тригонометрических уравнений
Уравнение 1. \( \displaystyle sin\left( x \right)=0,5\)
Запишу по определению:
\( \displaystyle x={{\left( -1 \right)}^{n}}\arcsin \left( 0,5 \right)+\pi n,~n\in Z\)
Всё готово, осталось только упростить, посчитав значение арксинуса.
Уравнение 2. \( \displaystyle sin\left( x \right)=-\frac{\sqrt{3}}{2}\)
Снова по определению:
Тогда запишу
\( \displaystyle x={{\left( -1 \right)}^{n}}\arcsin \left( -\frac{\sqrt{3}}{2} \right)+\pi n,~n\in Z\)
Так оставлять нельзя! Вначале вынесу «минус» из арксинуса!
Уравнение 3. \( \displaystyle sin\left( x \right)=\frac{\pi }{2}\)
Пример-ловушка! Невнимательный ученик бы записал ответ в лоб:
\( \displaystyle x={{\left( -1 \right)}^{n}}\arcsin \left( \frac{\pi }{2} \right)+\pi n,~n\in Z\)
Или того хуже:
\( \displaystyle x={{\left( -1 \right)}^{n}}\cdot 1+\pi n,~n\in Z\)
Так как \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\)
Но ты же внимательно читал мои пространные рассуждения, не так ли? И ты ведь не напишешь такую чушь? И ты понял, в чем здесь подвох?
А подвох вот в чем:
Уравнение 4. \( \displaystyle sin\left( x \right)=-0,1\)
По определению:
\( \displaystyle x={{\left( -1 \right)}^{n}}\arcsin \left( -0,1 \right)+\pi n,~n\in Z\)
Или вынесем минус (как в примере 2):
\( \displaystyle x={{\left( -1 \right)}^{n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
На этом стоп! Такого числа как 0,1 нет в таблице значений тригонометрических функций, поэтому оставим всё как есть:
Ответ: \( \displaystyle x={{\left( -1 \right)}^{n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
Уравнение 5. \( \displaystyle cos\left( x \right)=1\)
И снова по определению (теперь для уравнения другого вида)
\( \displaystyle x=\pm arccos1+2\pi n,~n\in Z\)
Чему равен угол, косинус которого равен \( \displaystyle 1\)?
Этот угол равен\( \displaystyle 0\)!
\( \displaystyle x=\pm 0+2\pi n,~n\in Z\)
Тогда нет смысла прибавлять или вычитать ноль, всё равно это ноль.
\( \displaystyle x=2\pi n,~n\in Z\)
Получили формулу, которая есть в таблице решений тригонометрических уравнений!
Ответ: \( \displaystyle x=2\pi n,~n\in Z\)
Уравнение 6. \( \displaystyle cos\left( x \right)=-\frac{1}{\sqrt{2}}\)
По определению:
\( \displaystyle x=\pm \arccos \left( -\frac{1}{\sqrt{2}} \right)+2\pi n,~n\in Z\)
Прежде всего вынесем «минус» по правилам для арккосинуса:
\( \displaystyle x=\pm \left( \pi -\arccos \left( \frac{1}{\sqrt{2}} \right) \right)+2\pi n,~n\in Z\)
Вот так и никак иначе выносится минус, запомни это!
Теперь арккосинус.
Не во всех таблицах есть значение \( \displaystyle \frac{1}{\sqrt{2}}\), но во всех есть \( \displaystyle \frac{\sqrt{2}}{2}\)!!!
А теперь, внимание, ловкость рук и никакого мошенничества!
Уравнение 7. \( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
Ещё один пример-обманка! Хотя данное уравнение решения имеет, ибо:
\( \displaystyle \frac{\pi }{4}=\frac{3,14}{4}<1\)
Тогда по определению:
\( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
Но из этого никак не следует, что \( \displaystyle \arccos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2}\)!!!!!!
Запомни, арккосинус – это угол, его аргумент (начинка) – это число, а выход – угол!!!
Ты когда-нибудь встречал в своей практике такой странный угол как \( \displaystyle \frac{\sqrt{2}}{2}\)?!
Вот и я нет. Поэтому оставим как есть!
Ответ: \( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
Уравнение 8. \( \displaystyle cos\left( x \right)=-\sqrt{2}\)
Всё просто: \( \displaystyle -\sqrt{2}<-1\)
… и решений данное уравнение не имеет.
Уравнение 9. \( \displaystyle tg\left( x \right)=\sqrt{2}\)
Запишем по определению:
\( \displaystyle x=arctg\sqrt{2}+\pi n,~n\in Z\)
\( \displaystyle arctg\sqrt{2}\) – не табличное значение, поэтому ответ сохраняем неизменным.
Обрати внимание, что в отличие от уравнений с синусом и косинусом, здесь мне не уже важно, какое у меня число стоит в правой части уравнения.
Уравнение 10. \( \displaystyle ctg\left( x \right)=-\sqrt{3}\)
Снова по определению:
\( \displaystyle x=arсctg\left( -\sqrt{3} \right)+\pi n,~n\in Z\)
Без проблем выносим минус из арккотангенса:
Уравнение 11. \( \displaystyle ctg\left( x \right)=1\)
По формуле: \( \displaystyle x=arcctg1+\pi n,~n\in Z\).
Котангенс какого угла равен \( \displaystyle 1\)?
Это угол \( \displaystyle \frac{\pi }{4}\).
Ответ: \( \displaystyle x=\frac{\pi }{4}+\pi n,~n\in Z\).
Ну как, материал не кажется тебе слишком сложным? Я надеюсь, что нет. Теперь давай порешаем для закрепления чуть более сложные задачки.
Решение 3-х более сложных уравнений
Уравнение 12. Найдите корни уравнения: \( \displaystyle cos\frac{8\pi x}{6}=\frac{\sqrt{3}}{2}\). В ответе запишите наибольший отрицательный корень.
Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!
Если бы мы решали уравнение вида:
\( \displaystyle cost=\frac{\sqrt{3}}{2}\)
То мы бы записали вот такой ответ:
\( \displaystyle t=\pm arccos\frac{\sqrt{3}}{2}+2\pi n,~n\in Z\)
Или (так как \( \displaystyle arccos\frac{\sqrt{3}}{2}=\frac{\pi }{6}\))
\( \displaystyle t=\pm \frac{\pi }{6}+2\pi n,~n\in Z\)
Но теперь в роли \( \displaystyle t\) у нас выступаем вот такое выражение: \( \displaystyle t=\frac{8\pi x}{6}\)
Тогда можно записать:
\( \displaystyle \frac{8\pi x}{6}=\pm \frac{\pi }{6}+2\pi n\)
Наша с тобою цель – сделать так, чтобы слева стоял просто \( \displaystyle x\), без всяких «примесей»!
Давай постепенно от них избавляться!
Вначале уберём знаменатель при \( \displaystyle x\): для этого домножим наше равенство на \( \displaystyle 6\):
\( \displaystyle \frac{6\cdot 8\pi x}{6}=6\cdot \left( \pm \frac{\pi }{6}+2\pi n \right)\)
\( \displaystyle 8\pi x=\pm \frac{6\pi }{6}+12\pi n\)
\( \displaystyle 8\pi x=\pm \pi +12\pi n\)
Теперь избавимся от \( \displaystyle \pi \), разделив на него обе части:
\( \displaystyle 8x=\pm 1+12n\)
Теперь избавимся от восьмёрки:
\( \displaystyle \frac{8x}{8}=\pm \frac{1}{8}+\frac{12n}{8}\)
\( \displaystyle x=\pm \frac{1}{8}+\frac{3n}{2}\)
Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)
\( \displaystyle x=\frac{1}{8}+\frac{3n}{2}\)
или
\( \displaystyle x=-\frac{1}{8}+\frac{3n}{2}\)
Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать \( \displaystyle n\).
Рассмотрим вначале первую серию:
Уравнение 13. Найдите корни уравнения: \( \displaystyle cos\frac{\pi \left( {x}-7 \right)}{3}=\frac{1}{2}\). В ответ запишите наибольший отрицательный корень.
Опять решаем, не взирая на сложный аргумент косинуса:
\( \displaystyle \frac{\pi \left( {x}-7 \right)}{3}=\pm arccos\frac{1}{2}+2\pi n,~n\in Z\)
\( \displaystyle \frac{\pi \left( {x}-7 \right)}{3}=\pm \frac{\pi }{3}+2\pi n,~n\in Z\)
Теперь снова выражаем \( \displaystyle x\) слева:
Умножаем обе стороны на \( \displaystyle 3\)
\( \displaystyle \frac{3\pi \left( {x}-7 \right)}{3}=\pm \frac{3\pi }{3}+2\cdot 3\pi n,~n\in Z\)
\( \displaystyle \pi \left( {x}-7 \right)=\pm \pi +6\pi n,~n\in Z\)
Делим обе стороны на \( \displaystyle \pi\)
\( \displaystyle \frac{\pi \left( {x}-7 \right)}{\pi }=\pm \frac{\pi }{\pi }+\frac{6\pi n}{\pi },~n\in Z\)
\( \displaystyle ~{x}-7=\pm 1+6n,~n\in Z\)
Всё, что осталось, – это перенести \( \displaystyle 7\) вправо, изменив её знак с минуса на плюс.
\( \displaystyle x=7\pm 1+6n,~n\in Z\)
У нас опять получается 2 серии корней, одна с \( \displaystyle +1\), а другая с \( \displaystyle -1\).
\( \displaystyle x=8+6n,~n\in Z\)
или
\( \displaystyle x=6+6n,~n\in Z\)
Нам нужно найти наибольший отрицательный корень. Рассмотрим первую серию:
Уравнение 14. Решите уравнение \( \displaystyle tg\frac{\pi x}{4}=-1\). В ответе напишите наибольший отрицательный корень.
Решаем, не взирая на сложный аргумент тангенса.
Вот, вроде бы ничего сложного, не так ли?
\( \displaystyle \frac{\pi x}{4}=arctg\left( -1 \right)+\pi n\)
\( \displaystyle \frac{\pi x}{4}=-arctg\left( 1 \right)+\pi n\)
\( \displaystyle \frac{\pi x}{4}=-\frac{\pi }{4}+\pi n\)
Как и раньше, выражаем \( \displaystyle x\) в левой части:
\( \displaystyle \frac{4\pi x}{4}=-\frac{4\pi }{4}+4\pi n\)
\( \displaystyle \pi x=-\pi +4\pi n\)
\( \displaystyle \frac{\pi x}{\pi }=-\frac{\pi }{\pi }+\frac{4\pi n}{\pi }\)
\( \displaystyle x=-1+4n\)
Ну вот и замечательно, здесь вообще всего одна серия корней! Опять найдём наибольший отрицательный.
Ясно, что он получается, если положить \( \displaystyle n=0\). И корень этот равен \( \displaystyle -1\).
Ответ: \( \displaystyle -1\)
Теперь попробуй самостоятельно решить следующие задачи.
Решение 3-х примеров для самостоятельной работы
- Решите уравнение \( \displaystyle sin\frac{\pi x}{3}=0,5\). В ответе напишите наименьший положительный корень.
- Решите уравнение \( \displaystyle tg\frac{\pi \left( {x}-6 \right)}{6}=\frac{1}{\sqrt{3}}\). В ответе напишите наименьший положительный корень.
- Решите уравнение \( \displaystyle sin\frac{\pi \left( 2{x}-3 \right)}{6}=-0,5\). В ответе напишите наименьший положительный корень.
Готов? Проверяем. Я не буду подробно описывать весь алгоритм решения, мне кажется, ему и так уделено достаточно внимания выше.
Ну что же, теперь ты умеешь решать простейшие тригонометрические уравнения! Сверься с решениями и ответами:
Ну что, всё правильно? Ох уж эти гадкие синусы, с ними всегда какие-то беды!
Эти знания помогут тебе решать многие задачи, с которыми ты столкнёшься в экзамене.
Если же ты претендуешь на оценку «5», то тебе просто необходимо перейти к чтению статьи для среднего уровня, которая будет посвящена решению более сложных тригонометрических уравнений.
СРЕДНИЙ УРОВЕНЬ СЛОЖНОСТИ
В этой части статьи я опишу решение тригонометрических уравнений более сложного типа и объясню, как производить отбор их корней. Здесь я буду опираться на следующие темы:
- Тригонометрические уравнения для начального уровня (см. выше)
- Формулы тригонометрии
Рекомендую тебе прежде ознакомиться с ними, прежде чем приступать к чтению и разбору этого чтива. Итак, все готово? Прекрасно. Тогда вперед.
Более сложные тригонометрические уравнения – это основа задач повышенной сложности. В них требуется как решить само уравнение в общем виде, так и найти корни этого уравнения, принадлежащие некоторому заданному промежутку.
Решение тригонометрических уравнений сводится к двум подзадачам:
- Решение уравнения
- Отбор корней
Следует отметить, что второе требуется не всегда, но все же в большинстве примеров требуется производить отбор. А если же он не требуется, то тебе скорее можно посочувствовать – это значит, что уравнение достаточно сложное само по себе.
Мой опыт разбора задач повышенной сложности показывает, что они как правило делятся на вот такие 4 категории.
Четыре категории задач повышенной сложности
- Уравнения, сводящиеся к разложению на множители.
- Уравнения, сводящиеся к виду \( \displaystyle tgx=a\).
- Уравнения, решаемые заменой переменной.
- Уравнения, требующие дополнительного отбора корней из-за иррациональности или знаменателя.
Говоря по-простому: если тебе попалось одно из уравнений первых трех типов, то считай, что тебе повезло. Для них как правило дополнительно нужно подобрать корни, принадлежащие некоторому промежутку.
Если же тебе попалось уравнение 4 типа, то тебе повезло меньше: с ним нужно повозиться подольше и повнимательнее, зато довольно часто в нем не требуется дополнительно отбирать корни.
Тем не менее данный тип уравнений я буду разбирать в разделе для продвинутых, а эту посвящу решению уравнений первых трех типов.
Уравнения, сводящихся к разложению на множители
Самое важное, что тебе нужно помнить, чтобы решать уравнения этого типа, это:
Как показывает практика, как правило, этих знаний достаточно. Давай обратимся к примерам.
Уравнения, сводящиеся к разложению с помощью синуса двойного угла:
Уравнение 18. Решите уравнение \( \displaystyle sin2x=\text{sin}\left( \frac{\pi }{2}+x \right)\). Найдите все корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ -\frac{7\pi }{2},-\frac{5\pi }{2} \right]\)
Здесь, как я и обещал, работают формулы приведения:
\( \displaystyle \sin \left( \frac{\pi }{2}+x \right)=cosx\)
Тогда мое уравнение примет вот такой вид:
\( \displaystyle sin2x=cosx\)
Что дальше? А дальше обещанный мною второй пункт программы – синус двойного угла:
\( \displaystyle sin2x=2sinxcosx\)
Тогда мое уравнение примет следующую форму:
\( \displaystyle 2sinxcosx=cosx\)
Недальновидный ученик мог бы сказать: а теперь я сокращу обе части на \( \displaystyle cosx\), получаю простейшее уравнение \( \displaystyle 2sinx=1\) и радуюсь жизни! И будет горько заблуждаться!
Запомни!
Никогда нельзя сокращать обе части тригонометрического уравнения на функцию, содержащую неизвестную! Таки образом ты теряешь корни!
Так что же делать? Да все просто, переносить все в одну сторону и выносить общий множитель:
\( \displaystyle 2sinxcosx-cosx=0\)
\( \displaystyle cosx\left( 2sinx-1 \right)=0\)
Ну вот, на множители разложили, ура! Теперь решаем:
\( \displaystyle cosx=0\) или \( \displaystyle 2sinx=1\)
Первое уравнение имеет корни:
\( \displaystyle x=\frac{\pi }{2}+\pi n\).
А второе:
\( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{6}+\pi n\)
На этом первая часть задачи решена. Теперь нужно отобрать корни.
Уравнения, сводящиеся к разложению на множители с помощью формул приведения
Уравнение 19. Решите уравнение \( \displaystyle 2si{{n}^{2}}x=\cos \left( \frac{3\pi }{2}-x \right)\). Найдите все корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ -\frac{5\pi }{2},-\pi \right]\).
Решение:
Опять пресловутые формулы приведения:
\( \displaystyle \cos \left( \frac{3\pi }{2}-x \right)=-sinx\)
\( \displaystyle 2si{{n}^{2}}x=-sinx\)
Опять не вздумай сокращать!
\( \displaystyle 2si{{n}^{2}}x+sinx=0\)
\( \displaystyle sinx\left( 2sinx+1 \right)=0\)
Откуда:
\( \displaystyle sinx=0\) или \( \displaystyle 2sinx+1=0,~sinx=-\frac{1}{2}\)
Первое уравнение имеет корни:
\( \displaystyle x=\pi n\)
А второе:
\( \displaystyle x={{\left( -1 \right)}^{n+1}}\frac{\pi }{6}+\pi n\)
Теперь снова поиск корней.
Уравнение 20. Решите уравнение \( \displaystyle \sqrt{2}\sin \left( \frac{3\pi }{2}-x \right)\cdot sinx=cosx\)
Найдите все корни этого уравнения, принадлежащие промежутку \( \displaystyle \left[ \frac{\pi }{2},\frac{3\pi }{2} \right]\).
И снова формула приведения:
\( \displaystyle ~\sin \left( \frac{3\pi }{2}-x \right)=-cosx\)
\( \displaystyle -\sqrt{2}cosxsinx=cosx\)
\( \displaystyle -\sqrt{2}cosxsinx-cosx=0\)
\( \displaystyle \sqrt{2}cosxsinx+cosx=0\)
\( \displaystyle cosx\left( \sqrt{2}sinx+1 \right)=0\)
\( \displaystyle cosx=0\) или \( \displaystyle \sqrt{2}sinx+1=0\)
\( \displaystyle sinx=-\frac{1}{\sqrt{2}}\)
Первая серия корней:
\( \displaystyle x=\frac{\pi }{2}+\pi n\).
Вторая серия корней:
Уравнение 20. Решите уравнение \( \displaystyle 2sin2x=4cosx-sinx+1\)
Укажите корни уравнения, принадлежащие отрезку \( \displaystyle \left[ -5\pi ,-4\pi \right]\)
Довольно хитрая группировка на множители (применю формулу синуса двойного угла):
\( \displaystyle 2\cdot 2sinxcosx=4cosx-sinx+1\)
\( \displaystyle 4sinxcosx-4cosx+sinx-1=0\)
\( \displaystyle 4cosx\left( sinx-1 \right)+\left( sinx-1 \right)=0\)
\( \displaystyle \left( 4cosx+1 \right)\left( sinx-1 \right)=0\)
тогда \( \displaystyle 4cosx+1=0\) или \( \displaystyle \left( sinx-1 \right)=0\)
\( \displaystyle cosx=-\frac{1}{4}\) или \( \displaystyle sinx=1\)
\( \displaystyle x=\pm \left( \pi -arccos\frac{1}{4} \right)+2\pi n\) или \( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{2}+\pi n\)
Это общее решение. Теперь надо отбирать корни. Беда в том, что мы не можем сказать точное значение угла, косинус которого равен одной четверти. Поэтому я не могу просто так избавиться от арккосинуса – вот такая досада!
Что я могу сделать?
Я могу прикинуть, что так как \( \displaystyle \frac{1}{4}<0,5\), то \( \displaystyle arccos\frac{1}{4}>\frac{\pi }{3}\).
\( \displaystyle \frac{\pi }{2}>arccos\frac{1}{4}>\frac{\pi }{3}\)
Составим таблицу: промежуток: \( \displaystyle \left[ -5\pi ;~-4\pi \right]\)
Уравнение 21. Решите уравнение \( \displaystyle sin2x-2\sqrt{3}si{{n}^{2}}x+4cosx-4\sqrt{3}sinx=0\). Найдите все корни этого уравнения, принадлежащие промежутку \( \displaystyle ~\left[ -\frac{\pi }{2},\pi \right]\).
Уравнение пугающего вида. Однако решается довольно просто путем применения формулы синуса двойного угла:
\( \displaystyle 2sinxcosx-2\sqrt{3}si{{n}^{2}}x+4cosx-4\sqrt{3}sinx=0\)
Сократим на 2:
\( \displaystyle sinxcosx-\sqrt{3}si{{n}^{2}}x+2cosx-2\sqrt{3}sinx=0\)
Сгруппируем первое слагаемое со вторым и третье с четвертым и вынесем общие множители:
\( \displaystyle sinx\left( cosx-\sqrt{3}sinx \right)+2\left( cosx-\sqrt{3}sinx \right)=0\)
\( \displaystyle \left( sinx+2 \right)\left( cosx-\sqrt{3}sinx \right)=0\)
\( \displaystyle sinx+2=0\) или \( \displaystyle cosx-\sqrt{3}sinx=0\)
Ясно, что первое уравнение корней не имеет, а теперь рассмотрим второе:
\( \displaystyle cosx-\sqrt{3}sinx=0\)
Вообще я собирался чуть позже остановиться на решении таких уравнений, но раз уж подвернулось, то делать нечего, надо решать…
Уравнения, сводящиеся к виду tgx=a
Ну вот, теперь самое время переходить ко второй порции уравнений, тем более, что я уже и так проболтался в чем состоит решение тригонометрических уравнений нового типа.
Но не лишним будет повторить, что уравнение вида
\( \displaystyle \text{acosx}+\text{bsinx}=0\text{ }\!\!~\!\!\text{ }\left( \text{a},\text{b}\ne 0 \right)\)
Решается делением обеих частей на косинус:
\( \displaystyle \text{a}\frac{\text{cosx}}{\text{cosx}}+\text{b}\frac{\text{sinx}}{\text{cosx}}=0\)
\( \displaystyle \text{a}+\text{btgx}=0\)
\( \displaystyle \text{tgx}=-\frac{\text{a}}{\text{b}}\)
Таким образом, решить уравнение вида
\( \displaystyle \text{acosx}+\text{bsinx}=0 \)
все равно, что решить
\( \displaystyle \text{tgx}=-\frac{\text{a}}{\text{b}}\)
Мы только что рассмотрели, как это происходит на практике. Однако давай решим еще и вот такие примеры.
Разбор 3-х примеров для закрепления материала
Уравнение 22. Решите уравнение \( \displaystyle sinx+si{{n}^{2}}\frac{x}{2}=co{{s}^{2}}\frac{x}{2}\). Укажите корни уравнения, принадлежащие отрезку \( \displaystyle \left[ -2\pi ,-\frac{\pi }{2} \right]\).
Решение:
Ну совсем простое. Перенесем \( \displaystyle si{{n}^{2}}\frac{x}{2}\) вправо и применим формулу косинуса двойного угла:
\( \displaystyle sinx=co{{s}^{2}}\frac{x}{2}-si{{n}^{2}}\frac{x}{2}\)
\( \displaystyle sinx=cosx\)
Ага! Уравнение вида:
\( \displaystyle acosx+bsinx=0\).
Делю обе части на \( \displaystyle cosx\)
\( \displaystyle \frac{sinx}{cosx}=\frac{cosx}{cosx}\)
\( \displaystyle tgx=1\)
\( \displaystyle x=\frac{\pi }{4}+\pi n\)
Делаем отсев корней:
Уравнение 23. Решите уравнение \( \displaystyle cosx={{\left( cos\frac{x}{2}-sin\frac{x}{2} \right)}^{2}}-1\). Укажите корни уравнения, принадлежащие промежутку \( \displaystyle \left[ \frac{\pi }{2},2\pi \right]\).
Все тоже довольно тривиально: раскроем скобки справа:
\( \displaystyle cosx=co{{s}^{2}}\frac{x}{2}-2sin\frac{x}{2}cos\frac{x}{2}+si{{n}^{2}}\frac{x}{2}-1\)
Основное тригонометрическое тождество:
\( \displaystyle co{{s}^{2}}\frac{x}{2}+si{{n}^{2}}\frac{x}{2}=1\)
Синус двойного угла:
\( \displaystyle 2sin\frac{x}{2}cos\frac{x}{2}=sinx\)
Окончательно получим:
Уравнение 24. Решите уравнение \( \displaystyle \sqrt{3}sin2x+3cos2x=0\). Найдите все корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ \frac{3\pi }{2},3\pi \right]\).
Уравнение решается сразу же, достаточно поделить обе части на \( \displaystyle cos2x\):
\( \displaystyle \sqrt{3}tg2x+3=0\)
\( \displaystyle \sqrt{3}tg2x=-3\)
\( \displaystyle tg2x=-\frac{3}{\sqrt{3}}\)
\( \displaystyle 2x=-\frac{\pi }{3}+\pi n\)
\( \displaystyle x=-\frac{\pi }{6}+\frac{\pi n}{2}\)
Отсев корней:
| \( \displaystyle n\) | \( \displaystyle x=-\frac{\pi }{6}+\frac{\pi n}{2}\) |
|---|---|
| \( \displaystyle 3\) | \( \displaystyle -\frac{\pi }{6}+\frac{3\pi }{2}\) — маленький недолет на \( \displaystyle \frac{\pi }{6}\) |
| \( \displaystyle 4\) | \( \displaystyle -\frac{\pi }{6}+2\pi =\frac{11\pi }{6}\) — попал! |
| \( \displaystyle 5\) | \( \displaystyle -\frac{\pi }{6}+\frac{5\pi }{2}=\frac{7\pi }{3}\) — снова в яблочко! |
| \( \displaystyle 6\) | \( \displaystyle -\frac{\pi }{6}+3\pi =\frac{17\pi }{6}\) — и снова удача на нашей стороне! |
| \( \displaystyle 7\) | \( \displaystyle -\frac{\pi }{12}+\frac{7\pi }{2}\) — на сей раз уже перелет! |
Ответ: \( \displaystyle \frac{11\pi }{6};\frac{14\pi }{6};\frac{17\pi }{6}\).
Так или иначе, нам еще предстоит встретиться с уравнениями того вида, которые мы только что разобрали. Однако нам еще рано закругляться: остался еще один «пласт» уравнений, которые мы не разобрали. Итак:
Решение тригонометрических уравнений заменой переменной
Здесь все прозрачно: смотрим пристально на уравнение, максимально его упрощаем, делаем замену, решаем, делаем обратную замену!
На словах все очень легко. Давай посмотрим на деле:
Уравнение 25. Решить уравнение: \( \displaystyle 4co{{s}^{4}}x-4co{{s}^{2}}x+1=0\). Найдите все корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ -2\pi ,-\pi \right]\).
Ну что же, здесь замена сама напрашивается к нам в руки!
\( \displaystyle t=co{{s}^{2}}x\)
Тогда наше уравнение превратится вот в такое:
Уравнение 26. Решите уравнение \( \displaystyle 6si{{n}^{2}}x+sin2x=2\). Укажите корни данного уравнения, принадлежащие промежутку \( \displaystyle \left[ \frac{3\pi }{2},\frac{5\pi }{2} \right]\).
Решение:
Здесь замена сразу не видна, более того, она не очень очевидна. Давай вначале подумаем: а что мы можем сделать?
Можем, например, представить
\( \displaystyle sin2x=2sinxcosx\)
А заодно и
\( \displaystyle 2=2si{{n}^{2}}x+2co{{s}^{2}}x\)
Тогда мое уравнение примет вид:
\( \displaystyle 6si{{n}^{2}}x+2sinxcosx=2si{{n}^{2}}x+2co{{s}^{2}}x\)
\( \displaystyle 4si{{n}^{2}}x+2sinxcosx-2co{{s}^{2}}x=0\)
\( \displaystyle 2si{{n}^{2}}x+sinxcosx-co{{s}^{2}}x=0\)
А теперь внимание, фокус:
Давай разделим обе части уравнения на \( \displaystyle co{{s}^{2}}x\):
\( \displaystyle 2\frac{si{{n}^{2}}x}{co{{s}^{2}}x}+\frac{sinxcosx}{co{{s}^{2}}x}-\frac{co{{s}^{2}}x}{co{{s}^{2}}x}=0\)
\( \displaystyle 2t{{g}^{2}}x+tgx-1=0\)
Внезапно мы с тобой получили квадратное уравнение относительно \( \displaystyle tgx\)!
Сделаем замену \( \displaystyle t=tgx\), тогда получим:
\( \displaystyle 2{{t}^{2}}+t-1=0\)
Уравнение имеет следующие корни:
\( \displaystyle {{t}_{1}}=-1,{{t}_{2}}=\frac{1}{2}\)
Отсюда:
\( \displaystyle tgx=-1\).
\( \displaystyle x=-\frac{\pi }{4}+\pi n\)
Или
\( \displaystyle tgx=\frac{1}{2}\).
\( \displaystyle x=arctg\frac{1}{2}+\pi n\)
Неприятная вторая серия корней, но ничего не поделаешь!
Производим отбор корней на промежутке \( \displaystyle \left[ \frac{3\pi }{2},\frac{5\pi }{2} \right]\).
Нам также нужно учитывать, что:
Уравнение 27. Решите уравнение \( \displaystyle \frac{1}{t{{g}^{2}}x}+\frac{3}{sinx}+3=0\). Найдите все корни этого уравнения, принадлежащие промежутку \( \displaystyle \left[ 2\pi ,\frac{7\pi }{2} \right]\).
Решение:
Здесь нужно держать ухо востро: у нас появились знаменатели, которые могут быть нулевыми! Поэтому надо быть особо внимательными к корням!
Прежде всего, мне нужно преобразовать уравнение так, чтобы я мог сделать подходящую замену. Я не могу придумать сейчас ничего лучше, чем переписать тангенс через синус и косинус:
\( \displaystyle t{{g}^{2}}x=\frac{si{{n}^{2}}x}{co{{s}^{2}}x}\)
\( \displaystyle \frac{co{{s}^{2}}x}{si{{n}^{2}}x}+\frac{3}{sinx}+3=0\)
Теперь я перейду от косинуса к синусу по основному тригонометрическому тождеству:
\( \displaystyle \frac{1-si{{n}^{2}}x}{si{{n}^{2}}x}+\frac{3}{sinx}+3=0\)
И, наконец, приведу все к общему знаменателю:
\( \displaystyle \frac{1-si{{n}^{2}}x}{si{{n}^{2}}x}+\frac{3sinx}{si{{n}^{2}}x}+\frac{3si{{n}^{2}}x}{si{{n}^{2}}x}=0\)
\( \displaystyle \frac{1-si{{n}^{2}}x+3sinx+3si{{n}^{2}}x}{si{{n}^{2}}x}=0\)
\( \displaystyle \frac{2si{{n}^{2}}x+3sinx+1}{si{{n}^{2}}x}=0\)
Теперь я могу перейти к уравнению:
\( \displaystyle 2si{{n}^{2}}x+3sinx+1=0\)
Но при \( \displaystyle si{{n}^{2}}x\ne 0\) (то есть при \( \displaystyle x\ne \pi n\)).
Теперь все готово для замены: \( \displaystyle t=sin x\)
Уравнение 28. Решите уравнение \( \displaystyle 4si{{n}^{2}}x+8\sin \left( \frac{3\pi }{2}+x \right)+1=0\)
Найдите все корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ -3\pi ,-\frac{3\pi }{2} \right]\).
Работаем по формулам приведения:
\( \displaystyle \sin \left( \frac{3\pi }{2}+x \right)=-cosx\)
Подставляем в уравнение:
\( \displaystyle 4si{{n}^{2}}x+8\left( -cosx \right)+1=0\)
Перепишем все через косинусы, чтобы удобнее было делать замену:
\( \displaystyle 4\left( 1-co{{s}^{2}}x \right)-8cosx+1=0\)
\( \displaystyle -4co{{s}^{2}}x-8cosx+5=0\)
\( \displaystyle 4co{{s}^{2}}x+8cosx-5=0\)
Теперь легко сделать замену:
\( \displaystyle t=cosx\)
\( \displaystyle 4{{t}^{2}}+8t-5=0\)
\( \displaystyle {{t}_{1}}=-\frac{5}{2},{{t}_{2}}=\frac{1}{2}\)
Ясно, что \( \displaystyle {{t}_{1}}=-\frac{5}{2}\) — посторонний корень, так как уравнение \( \displaystyle cosx=-\frac{5}{2}\) решений не имеет.
Уравнение 30. Решите уравнение \( \displaystyle t{{g}^{2}}x+\left( 1+\sqrt{3} \right)tgx+\sqrt{3}=0\)
Укажите корни этого уравнения, принадлежащие отрезку \( \displaystyle \left[ \frac{5\pi }{2},4\pi \right]\).
Здесь замена видна сразу: \( \displaystyle t=tgx\)
\( \displaystyle {{t}^{2}}+\left( 1+\sqrt{3} \right)t+\sqrt{3}=0\)
\( \displaystyle {{t}_{1}}=-1,~{{t}_{2}}=-\sqrt{3}\)
Тогда \( \displaystyle tgx=-1\) или \( \displaystyle tgx=-\sqrt{3}\)
\( \displaystyle x=-\frac{\pi }{4}+\pi n\)
или
\( \displaystyle x=-\frac{\pi }{3}+\pi n\)
Отбор корней на промежутке \( \displaystyle \left[ \frac{5\pi }{2},4\pi \right]\):
\( \displaystyle n\)
\( \displaystyle x=-\frac{\pi }{4}+\pi n\)
\( \displaystyle x=-\frac{\pi }{3}+\pi n\)
\( \displaystyle 3\)
\( \displaystyle x=\frac{11\pi }{4}\) — подходит!
\( \displaystyle x=\frac{8\pi }{3}\) — подходит!
\( \displaystyle 4\)
\( \displaystyle x=\frac{15\pi }{4}\) — подходит!
\( \displaystyle x=\frac{11\pi }{3}\) — подходит!
\( \displaystyle 5\)
\( \displaystyle x=\frac{19\pi }{4}\) — много!
\( \displaystyle x=\frac{14\pi }{3}\) — тоже много!
Ответ: \( \displaystyle \frac{11\pi }{4};\ \frac{8\pi }{3};\ \frac{15\pi }{4};\ \frac{11\pi }{3}\)
Ну вот, теперь все! Но решение тригонометрических уравнений на этом не заканчивается, за бортом у нас остались самые сложные случаи: когда в уравнениях присутствует иррациональность или разного рода «сложные знаменатели».
Как решать подобные задания мы рассмотрим далее в разделе для продвинутого уровня.
ПРОДВИНУТЫЙ УРОВЕНЬ СЛОЖНОСТИ
Уравнения, требующие дополнительного отбора корней из-за иррациональности и знаменателя
В дополнение к рассмотренным в предыдущих двух статьях тригонометрическим уравнениям, рассмотрим еще один класс уравнений, которые требуют еще более внимательного анализа.
Данные тригонометрические примеры содержат либо иррациональность, либо знаменатель, что делает их анализ более сложным.
Тем не менее ты вполне можешь столкнуться с данными уравнениями на ЕГЭ (и получить за них максимальное количество баллов!).
Однако нет худа без добра: для таких уравнений уже, как правило, не ставится вопрос о том, какие из его корней принадлежат заданному промежутку.
Давай не будем ходить вокруг да около, а сразу тригонометрические примеры.
Уравниние 31. Решить уравнение \( \displaystyle \frac{2si{{n}^{2}}x+sinx}{2cosx-\sqrt{3}}=0~\) и найти те корни, которые принадлежат отрезку \( \displaystyle \left[ -\frac{3\pi }{2},0 \right]\).
Решение:
У нас появляется знаменатель, который не должен быть равен нулю! Тогда решить данное уравнение – это все равно, что решить систему
\( \displaystyle \left\{ \begin{array}{l}2si{{n}^{2}}x+sinx=0\\2cosx-\sqrt{3}\ne 0\end{array} \right.\)Решим каждое из уравнений:
\( \displaystyle 2si{{n}^{2}}x+sinx=0\)
\( \displaystyle sinx\left( 2sinx+1 \right)=0\)
\( \displaystyle sinx=0\) или \( \displaystyle sinx=-\frac{1}{2}\)
\( \displaystyle x=\pi n\) или \( \displaystyle x={{\left( -1 \right)}^{n+1}}\frac{\pi }{6}+\pi n\)
А теперь второе:
\( \displaystyle 2cosx-\sqrt{3}\ne 0\)
\( \displaystyle x\ne \pm \frac{\pi }{6}+2\pi n\)
или \( \displaystyle x\ne \frac{\pi }{6}+2\pi n\), \( \displaystyle x\ne -\frac{\pi }{6}+2\pi n\)
Теперь давай посмотрим на серию:
Уравнение 32. Решите уравнение: \( \displaystyle \left( sinx-\frac{\sqrt{3}}{2} \right)\sqrt{3{{x}^{2}}-7x+4}=0\)
Решение:
Ну хотя бы не надо отбирать корни и то хорошо! Давай вначале решим уравнение, не взирая на иррациональность:
\( \displaystyle sinx=\frac{\sqrt{3}}{2}\)
\( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{3}+\pi n\)
\( \displaystyle 3{{x}^{2}}-7x+4=0\)
\( \displaystyle {{x}_{1}}=1,{{x}_{2}}=\frac{4}{3}\)
И что, это все? Нет, увы, так было бы слишком просто! Надо помнить, что под корнем могут стоять только неотрицательные числа. Тогда:
\( \displaystyle 3{{x}^{2}}-7x+4\ge 0\)
Решение этого неравенства:
Уравнение 33. \( \displaystyle \left( 2{{x}^{2}}-5x+2 \right)\sqrt{cosx-\sqrt{3}sinx}=0\)
Как и раньше: вначале решим каждое отдельно, а потом подумаем, что же мы наделали.
\( \displaystyle 2{{x}^{2}}-5x+2=0\)
\( \displaystyle {{x}_{1}}=2,~{{x}_{2}}=0,5\)
Теперь второе уравнение:
\( \displaystyle cosx-\sqrt{3}sinx=0\)
\( \displaystyle tgx=\frac{1}{\sqrt{3}}\)
\( \displaystyle x=\frac{\pi }{6}+\pi n\)
Теперь самое сложное – выяснить, не получаются ли отрицательные значения под арифметическим корнем, если мы подставим туда корни из первого уравнения:
\( \displaystyle cos2-\sqrt{3}sin2\)
Число \( \displaystyle 2\) надо понимать как \( \displaystyle 2\) радианы.
Так как \( \displaystyle 1\) радиана – это примерно \( \displaystyle 57\) градусов, то \( \displaystyle 2\) радианы – порядка \( \displaystyle 114\) градусов. Это угол второй четверти.
Косинус второй четверти имеет какой знак? Минус. А синус? Плюс. Так что можно сказать про выражение
\( \displaystyle cos2-\sqrt{3}sin2\)?
Оно меньше нуля!
\( \displaystyle cos2-\sqrt{3}sin2<0\)
А значит \( \displaystyle 2\) – не является корнем уравнения.
Теперь черед \( \displaystyle \frac{1}{2}\).
\( \displaystyle cos\frac{1}{2}-\sqrt{3}sin\frac{1}{2}\)
Сравним это число с нулем.
Уравнение 34. \( \displaystyle \left( 4co{{s}^{2}}x-4cosx-3 \right)\sqrt{-6sinx}=0\)
Решение:
\( \displaystyle 4co{{s}^{2}}x-4cosx-3=0\)
\( \displaystyle t=cosx\)
\( \displaystyle 4{{t}^{2}}-4t-3=0\)
\( \displaystyle {{t}_{1}}=-0,5;{{t}_{2}}=1,5\) – корень \( \displaystyle {{t}_{2}}\) не годится, ввиду ограниченности косинуса
\( \displaystyle cosx=-0,5\)
\( \displaystyle x=\pm \frac{2\pi }{3}+2\pi n\)
Теперь второе:
Уравнение 35. \( \displaystyle \frac{cos2x+sinx}{\sqrt{\text{sin}\left( x-\frac{\pi }{4} \right)}}=0\)
Ну, ничего не поделаешь – поступаем так, как и раньше.
\( \displaystyle cos2x+sinx=0\)
\( \displaystyle 1-2si{{n}^{2}}x+sinx=0\)
\( \displaystyle 2si{{n}^{2}}x-sinx-1=0\)
\( \displaystyle t=sinx\)
\( \displaystyle 2{{t}^{2}}-t-1=0\)
\( \displaystyle {{t}_{1}}=-0,5,{{t}_{2}}=1\)
\( \displaystyle sinx=-0,5\) или \( \displaystyle sinx=1\)
\( \displaystyle x={{\left( -1 \right)}^{n+1}}\frac{\pi }{6}+\pi n\) или \( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{2}+\pi n\)
Теперь работаем со знаменателем:
\( \displaystyle \text{sin}\left( x-\frac{\pi }{4} \right)\ge 0\)
Я не хочу решать тригонометрическое неравенство, а потому поступлю хитро: возьму и подставлю в неравенство мои серии корней:
Уравнение 36. \( \displaystyle \sqrt{9-{{x}^{2}}}cosx=0\)
Первое уравнение: \( \displaystyle 9-{{x}^{2}}=0\)
\( \displaystyle x=3\) или \( \displaystyle x=-3\)
ОДЗ корня:
\( \displaystyle 9-{{x}^{2}}\ge 0\)
\( \displaystyle x\in \left[ -3;3 \right]\)
Второе уравнение:
Уравнение 37. \( \displaystyle \frac{2si{{n}^{2}}x-sinx}{2cosx-\sqrt{3}}=0\)
\( \displaystyle 2si{{n}^{2}}x-sinx=0\)
\( \displaystyle sinx\left( 2sinx-1 \right)=0\)
\( \displaystyle sinx=0\) или \( \displaystyle sinx=0,5\)
\( \displaystyle x=\pi n\) или \( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{6}+\pi n\)
Но \( \displaystyle 2cosx-\sqrt{3}\ne 0\)
\( \displaystyle cosx\ne \frac{\sqrt{3}}{2}\)
\( \displaystyle x\ne \pm \frac{\pi }{6}+2\pi n\)
Рассмотрим \( \displaystyle x={{\left( -1 \right)}^{n}}\frac{\pi }{6}+\pi n\).
Если \( \displaystyle n\) – четное, то
\( \displaystyle x=\frac{\pi }{6}+2\pi k\) – не подходит!
Если \( \displaystyle n\) – нечетное, \( \displaystyle n=2k+1\):
\( \displaystyle x=-\frac{\pi }{6}+2\pi k+\pi =\frac{5\pi }{6}+2\pi k\) – подходит!
Значит, наше уравнение имеет такие серии корней:
\( \displaystyle x=\pi n\) или \( \displaystyle x=\frac{5\pi }{6}+2\pi n\)
Отбор корней на промежутке \( \displaystyle \left[ \frac{3\pi }{2},3\pi \right]\):
| \( \displaystyle n\) | \( \displaystyle 1\) | \( \displaystyle 2\) | \( \displaystyle 3\) |
|---|---|---|---|
| \( \displaystyle x=\pi n\) | \( \displaystyle \pi \)— не подходит | \( \displaystyle 2\pi \) – подходит | \( \displaystyle 3\pi \) – подходит |
| \( \displaystyle x=\frac{5\pi }{6}+2\pi n\) | \( \displaystyle \frac{5\pi }{6}+2\pi =\frac{17\pi }{6}\) – подходит | \( \displaystyle \frac{5\pi }{6}+4\pi \) – много | много |
Ответ: \( \displaystyle 3\pi \), \( \displaystyle 2\pi \), \( \displaystyle \frac{17\pi }{6}\).
Уравнение 38. \( \displaystyle \left( 2co{{s}^{2}}x-cosx \right)\sqrt{-11tgx}=0\)
\( \displaystyle 2co{{s}^{2}}x-cosx=0\)
\( \displaystyle cosx\left( 2cosx-1 \right)=0\)
\( \displaystyle cosx=0~\)или \( \displaystyle 2cosx-1=0\)
Так как \( \displaystyle tgx=\frac{sinx}{cosx}\), то при \( \displaystyle cosx=0~\) тангенс не определен. Тут же отбрасываем эту серию корней!
\( \displaystyle 2cosx-1=0\)
\( \displaystyle cosx=0,5\)
\( \displaystyle x=\pm \frac{\pi }{3}+2\pi n\)
Вторая часть:
\( \displaystyle -11tgx=0\)
\( \displaystyle x=\pi n\)
В то же время по ОДЗ требуется, чтобы
\( \displaystyle tgx\le 0\)
Проверяем найденные в первом уравнении корни:
\( \displaystyle tg\left( \pm \frac{\pi }{3}+2\pi n \right)\le 0\)
Если знак \( \displaystyle +\):
\( \displaystyle tg\left( \frac{\pi }{3}+2\pi n \right)\le 0\)
\( \displaystyle \frac{\pi }{3}+2\pi n\) – углы первой четверти, где тангенс положительный. Не подходит!
Если знак \( \displaystyle —\):
\( \displaystyle tg\left( -\frac{\pi }{3}+2\pi n \right)\le 0\)
\( \displaystyle -\frac{\pi }{3}+2\pi n\) – угол четвертой четверти. Там тангенс отрицательный. Подходит. Записываем ответ:
Ответ: \( \displaystyle x=\pi n\), \( \displaystyle x=-\frac{\pi }{3}+2\pi n\).
Мы вместе разобрали в этой статье сложные тригонометрические примеры, но тебе стоит прорешать уравнения самому.
Подготовка к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



mne nravitsya☺️👍
Пока очень нравится. Надо посмотреть учебники по математике и физике. Интересно.
Это же и есть учебник по математике) А по физике написано всего несколько глав
» Спасибо» вам огромное. Позавчера я зарегистрировался на вашем сайте, один раз попользовался вашим учебником, а сегодня вы снова предлагаете мне зарегистрироваться.
Артем, у вас есть доступ ко всем статьям учебника, я проверил.
Прочитайте, пожалуйста, ВНИМАТЕЛЬНО И ДО КОНЦА, письмо, которое вы получили при регистрации. Вот что там написано:
«Примечание 1. Иногда настройки вашего браузера не позволяют видеть закрытый контент — зайдите с другого браузера.
Примечание 2. Еще одной причиной закрытого контента может быть то, что вы не авторизованы на сайте. В этом случае войдите в личный кабинет на главной странице сайта или здесь: https://youclever.org/my-account/.»
Спасибо огромное!
И вам спасибо!
Огромная благодарность за ваше супер объяснение!
Спасибо, Асыл! Приятно слышать!
Некоторые комментарии прошлых лет к этой статье:
Ксения
24 апреля 2018
Очень мощно все объясняете! Отличный материал. Я в восторге
Оксана
21 июня 2018
Я вообще не понимала ничего! Сейчас спокойно иду на экзамен! СПАСИБО)))
Олег
29 апреля 2019
Большое спасибо за статью, все понятно и на простом языке. Александр, очень хочется статью про параметр
Наташа
06 декабря 2019
Это было понятно, Спасибо!
Светлана
28 июня 2020
Для второго высшего планирую сдавать внутренние экзамены в ВУЗе. Отлично освежила в памяти решение тригонометрических уравнений. Все остальные темы также доходчиво объясняются?