Площадь круга
Существует множество сложных задач о площади круга и его частей: секторов, сегментов, пересечений.
После прочтения этой статьи они станут для тебя простыми!
А еще посмотри задачи на окружности (ЕГЭ 16) из нашего курса подготовки.
Поехали!
Площадь круга — коротко о главном
Основные формулы:
Площадь круга:
\( \displaystyle S=\pi {{R}^{2}}\)

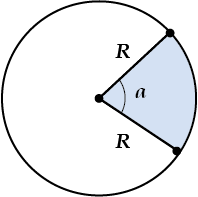
Площадь сектора:
\( \displaystyle S=\frac{a}{2}{{R}^{2}}\), где: \( \displaystyle a \) – величина угла сектора в радианах.
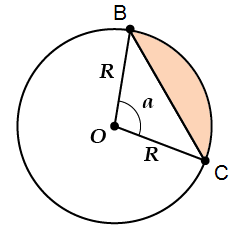
Площадь сегмента:
\( \displaystyle {{S}_{сегмента}}={{S}_{сектора}}-{{S}_{\Delta OBC}}\)
Правило нахождения нестандартной части круга:
Непонятную фигуру нужно разделить на несколько стандартных (сектор, сегмент, треугольник и т.д.), потом посчитать площадь каждой стандартной фигуры и сложить все площади.
Площадь круга — подробнее
\( \displaystyle \ S=\pi {{R}^{2}}\),
\( \displaystyle R\) — радиус,
\( \displaystyle \pi \) – число \( \displaystyle \approx 3,1415\)

Производит впечатление? Представляешь, сколько времени математики думали, пока не додумались, что…
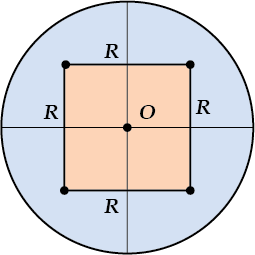
…площадь круга радиуса \( \displaystyle R\) ровно (!) в \( \displaystyle \pi \) раз больше площади квадрата со стороной \( \displaystyle R\).
Ну вот, а теперь – площадь части круга.
Площадь сектора круга
Смотри на картинку, это такая «хорошая» часть круга.
\( \displaystyle \ S=\frac{a}{2}{{R}^{2}}\),
где \( \displaystyle a \) – величина угла сектора в радианах (т.е. в числах \( \displaystyle \frac{\pi }{6}\), \( \displaystyle \frac{\pi }{4}\), \( \displaystyle \frac{\pi }{27}\) и т.д.)

Подробнее о радианах смотри в теме «Окружность. Вписанный угол».
Площадь сегмента круга
А это «плохая» часть круга – опять смотри на картинку:
\( \displaystyle \ {{S}_{сегмента}}={{S}_{сектора}}-{{S}_{\Delta OBC}}\)
\( \displaystyle \ S_{сегмента} \displaystyle=\frac{1}{2}{{R}^{2}}(\alpha -\sin \alpha )\),
но это и есть \( \displaystyle {{S}_{сегмента}}=\underbrace{{{S}_{сектора}}}_{\frac{1}{2}{{R}^{2}}\cdot \alpha }-\underbrace{{{S}_{\Delta OBC}}}_{\frac{1}{2}{{R}^{2}}\cdot \sin \alpha }\)
Площадь других частей круга
Иногда бывает, что нужно посчитать площадь какой-нибудь странной части круга. Эта часть может не быть ни сектором, ни сегментом.
Как тогда быть?
Давай рассмотрим два примера.
Пример 1
Окружности радиусов \( \displaystyle 2\) и \( \displaystyle 4\) пересекаются по хорде, равной \( \displaystyle 2\).
Найти площадь общей части кругов.
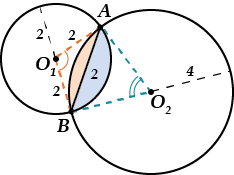
Решение:
Обрати внимание, что общая часть кругов состоит из двух сегментов: красного и голубого.
Найдем площадь голубого сегмента.
Для этого нужно посмотреть на окружность с центром \( \displaystyle {{O}_{1}}\).
\( \displaystyle \Delta A{{O}_{1}}B\) — правильный \( \displaystyle \quad \Rightarrow \ \angle A{{O}_{1}}B=\frac{\pi }{3}\,\, ({{60}^{\circ }})\).
Значит,
\( \displaystyle {{S}_{голубого\, сегм.}}=\frac{\pi }{6}\cdot {{2}^{2}}-\frac{{2}^{2}\sqrt{3}}{4}\ \)(это по формуле \( \displaystyle {{S}_{сегм.}}={{S}_{сектора}}-{{S}_{\Delta A{{O}_{1}}B}}\) ).
Если не помнишь, как считается площадь правильного треугольника, загляни в тему «Равносторонний треугольник».
Итак, \( \displaystyle {{S}_{голубого\, сегм.}}=\frac{2}{3}\pi -\sqrt{3}\)
\( \displaystyle {{S}_{красного\, сегм.}}={{S}_{сектора\ A{{O}_{2}}B}}-{{S}_{\Delta A{{O}_{2}}B}}\) \( \displaystyle {{S}_{\Delta A{{O}_{2}}B}}=\frac{1}{2}{O}_{2}K\cdot AB\) \( \displaystyle {O}_{2}K=\sqrt{A{O}_{2}^{2}-A{K}^{2}}=\sqrt{16-1}=\sqrt{15}\) \( \displaystyle {{S}_{A{{O}_{2}}B}}=\frac{1}{2}\cdot \sqrt{15}\cdot 2=\sqrt{15}.\)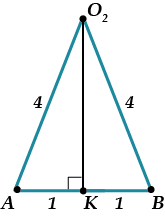
А вот найти \( \displaystyle \angle A{{O}_{2}}B\) уже сложнее.
Придется применять теорему косинусов!
\( \displaystyle A{{B}^{2}}=A{{O}_{2}}^{2}+{{O}_{2}}{{B}^{2}}-2A{{O}_{2}}\cdot {{O}_{2}}B\cdot \cos \angle A{{O}_{2}}B.\) \( \displaystyle \cos \angle A{{O}_{2}}B=\frac{A{{O}_{2}}^{2}+{{O}_{2}}{{B}^{2}}-A{{B}^{2}}}{2A{{O}_{2}}\cdot {{O}_{2}}B}=\frac{16+16-4}{2\cdot 16}=\frac{7}{8}.\) \( \displaystyle \Rightarrow \angle A{{O}_{2}}B=\arccos \frac{7}{8}.\)Подставляем:
\( \displaystyle {{S}_{кр.}}=\frac{\arccos \frac{7}{8}}{2}\cdot {{4}^{2}}-\sqrt{15}=8\cdot \arccos \frac{7}{8}-\sqrt{15}\)И теперь
\( \displaystyle S={{S}_{гол.}}+{{S}_{кр.}}=\frac{2}{3}\cdot \pi +8\cdot \arccos \frac{7}{8}-\sqrt{3}-\sqrt{15}.\)Пример 2
На стороне \( \displaystyle AB\) треугольника \( \displaystyle ABC\) как на диаметре построена окружность.
Найти площадь общей части треугольника и круга, если \( \displaystyle AB=4\), \( \displaystyle \angle A=30{}^\circ \), \( \displaystyle \angle B=140{}^\circ \).
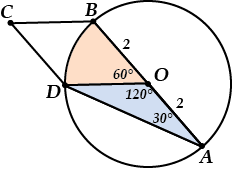
Решение:
Проведем \( \displaystyle OD\).
Опять наша непонятная фигура разделилась на две стандартные:
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
Перед вами вебинары, связанные с окружностями и 16 заданием ЕГЭ.
ЕГЭ 16 математика. Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности — это очень классный метод, но, к сожалению, он не всегда очевиден.
Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы — те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод — но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
ЕГЭ 16 Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
ЕГЭ 16. Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом.
Никуда не деться от окружностей — остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше — разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче).
Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники. Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org



Некоторые комментарии прошлых лет к этой статье:
Сережа
07 апреля 2019
Как рассчитать площадь треугольника с криволинейной (выпуклой дугой) гипотенузой? Размеры катетов и дуги известны.
Алексей Шевчук
04 сентября 2019
Сережа, проведи прямую гипотенузу, таким образом ты разобьёшь фигуру на 2 части. Вычисли площадь каждой из них, потом сложи.
Роберт
23 ноября 2019
Как найти площадь усеченной полу окружности?
Алексей Шевчук
24 ноября 2019
Роберт, разрежьте её на два сектора и треугольник, посчитайте площадь каждой части, потом сложите.
Владислав
26 января 2020
Как найти площадь наложенных друг на друга секторов, с центрами внутри одной окружности?
Алексей Шевчук
27 января 2020
Владислав, не совсем понятно, это секторы одной окружности, то есть с общим центром? Или центры не совпадают?
Нодир Юлдашев
09 июня 2020
Алексей, как можно посчитать, сколько процентов площади первого круга затмил второй круг исходя из того, сколько части диаметра первого круга затмил второй круг? Сейчас почитал про предстоящее кольцеобразное солнечное затмение 21 июня 2020 года и мне стало интересно. Диаметры кругов могут немножко отличаться из-за периодического изменения расстояния до Солнца и до Луны (в максимуме этого затмения видимый диаметр Солнца будет 31′ 28,4″ (0,524(5)°), а Луны — 30′ 48″ (0,51(3)°)). https://heavens-above.com/SolarEclipse.aspx?jdmax=2459021.77865012 (вкладка «Местные условия»)
Алексей Шевчук
09 июня 2020
Нодир, можно. Углы, которые здесь написаны, пропорциональны диаметрам (а значит, и радиусам) кругов. Отношение площадей равно квадрату отношения радиусов или диаметров (если поделить две формулы площади круга друг на друга, пи сокращается). Делим угловой диаметр Луны на Солнца, возводим в квадрат. Числа должны быть переведены в единицы измерения одного типа, например, в граусы: (0,513 / 0,525)^2 = 0.977^2 = 0.955 = 95.5%
Нодир Юлдашев
09 июня 2020
Алексей, спасибо за ответ, это тоже запомню, я хотел спросить о частичном затмении, которое у нас можно будет наблюдать. Луна подойдёт к Солнцу справа (с запада) и начинает его закрывать. В максимальной фазе Луна закроет 0,652 части диаметра Солнца (это величина (магнитуда) затмения) и 56,4% его площади (это максимальная фаза, %) (нижнюю часть Солнца). Центр Луны через центр Солнца у нас не пройдёт. Потом будет двигаться дальше налево (на восток) и выйдет из солнечного диска. Хотел поинтересоваться, а можно ли составить формулу для вычисления процента площади затмения исходя из величины (магнитуды) затмения. Я сам не школьник, я бухгалтер, и мне просто стало интересно. 🙂