Уравнение касательной к графику функции
Чтобы разобраться с этой темой, нужно знать что такое производная.
Сейчас проверим, знаешь ли ты ее… 🙂
Найди приращение функции \( y={{x}^{2}}+2x+3\) при приращении аргумента, равном \( \Delta x\).
Справился?
Должно получиться \( \Delta y=\Delta x\left( \Delta x+2x+2 \right)\).
А теперь найди производную функции \( y\left( x \right)=3{{\sin }^{2}}\sqrt{x}\) в точке \( {{x}_{0}}=\frac{{\pi }^{2}}{16}\).
Ответ: \( \frac{6}{\pi }\).
Получилось?
Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме «Производная» и проштудировать ее еще раз.
Знаю, тема очень большая, но иначе нет смысла идти дальше…
А если ты справился, то в путь!
Уравнение касательной к графику функции — коротко о главном
Геометрический смысл производной
Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:
\( {f}’\left( {{x}_{0}} \right)=\ {tg}\varphi =k\)
Уравнение касательной
Уравнение касательной к графику функции \( f\left( x \right)\) в точке \( {{x}_{0}}\):
\( y={f}’\left( {{x}_{0}} \right)\cdot \left( {x} -{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\).
Алгоритм действий для нахождения уравнения касательной
| Алгоритм | Пример: \( f\left( x \right)={{x}^{2}}-2x+3\), \( {{x}_{0}}=3\) |
| 1. Вычислим \( f\left( {{x}_{0}} \right)\) | \( f\left( {{x}_{0}} \right)=f\left( 3 \right)={{3}^{2}}-2\cdot 3+3=6\) |
| 2. Найдем формулу производной функции \( {f}’\left( x \right)\) | \( {f}’\left( x \right)={{\left( {{x}^{2}}-2x+3 \right)}^{\prime }}=2{x} -2\) |
| 3. Вычислим \( {f}’\left( {{x}_{0}} \right)\) | \( {f}’\left( {{x}_{0}} \right)={f}’\left( 3 \right)=2\cdot 3-2=4\) |
| 4. Подставим \( {{x}_{0}},\text{ }f\left( {{x}_{0}} \right)\) и \( {f}’\left( {{x}_{0}} \right)\) в формулу уравнения касательной \( y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\) | \( \begin{array}{l}y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)=\\\text{ }=4\left( x-3 \right)+6=4{x} -12+6=\\\text{ }=4{x} -6\end{array}\) |
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции \( y=f\left( x \right)\):
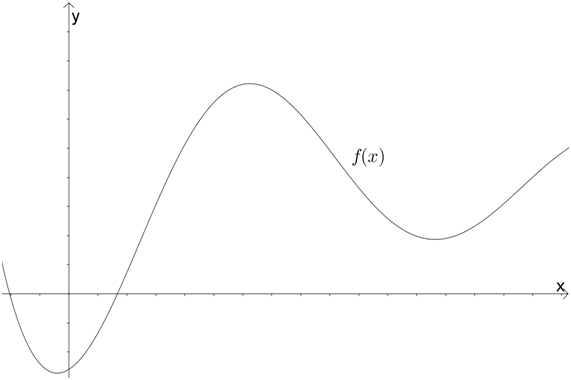
Выберем на линии графика некую точку \( A\). Пусть ее абсцисса \( {{x}_{0}}\), тогда ордината равна \( f\left( {{x}_{0}} \right)\).
Затем выберем близкую к точке \( A\) точку \( B\) с абсциссой \( {{x}_{0}}+\Delta x\); ее ордината – это \( f\left( {{x}_{0}}+\Delta x \right)\):
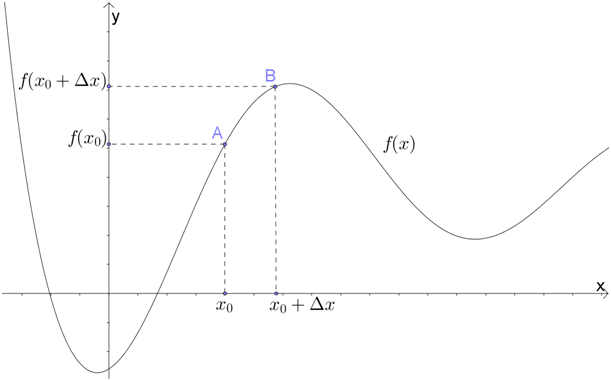
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси \( Ox\) как \( \alpha \).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол \( \alpha \)?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – \( 180{}^\circ \), а минимально возможный – \( 0{}^\circ \).
Значит, \( \alpha \in \left[ 0{}^\circ ;180{}^\circ \right)\). Угол \( 180{}^\circ \) не включается, поскольку положение прямой в этом случае в точности совпадает с \( 0{}^\circ \), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку \( C\), чтобы прямая \( AC\) была параллельна оси абсцисс, а \( BC\) – ординат:
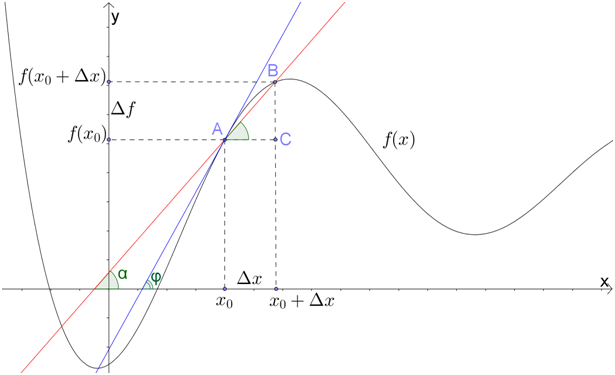
По рисунку видно, что \( AC=\Delta x\), а \( BC=\Delta f\).
Тогда отношение приращений:
\( \frac{\Delta f}{\Delta x}=\frac{BC}{AC}={tg}\alpha \)
(так как \( \angle C=90{}^\circ \), то \( \triangle ABC\) – прямоугольный).
Давай теперь уменьшать \( \Delta x\).
Тогда точка \( B\) будет приближаться к точке \( A\). Когда \( \Delta x\) станет бесконечно малым \( \left( \Delta x\to 0 \right)\), отношение \( \frac{\Delta f}{\Delta x}\) станет равно производной функции в точке \( {{x}_{0}}\).
Что же при этом станет с секущей?
Точка \( B\) будет бесконечно близка к точке \( A\), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки \( A\), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси \( \displaystyle Ox\) назовем \( \varphi \). Тогда получится, что производная
\( {f}’\left( {{x}_{0}} \right)\underset{\Delta x\to 0}{\mathop{=}}\,\frac{\Delta f}{\Delta x}=\ {tg}\varphi \),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
\( y=kx+b\).
За что отвечает коэффициент \( \displaystyle k\)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью \( \displaystyle Ox\)!
То есть вот что получается:
\( {f}’\left( {{x}_{0}} \right)=\ {tg}\varphi =k\).
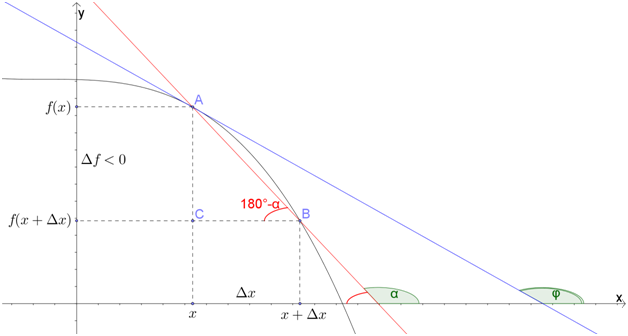
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы \( \alpha \) и \( \displaystyle \varphi \) тупые. А приращение функции \( \Delta f\) – отрицательное.
Снова рассмотрим \( \triangle ABC\): \( \angle B=180{}^\circ -\alpha \text{ }\Rightarrow \text{ }\ {tg}\angle B=-\ {tg}\alpha \).
С другой стороны, \( \ {tg}\angle B=\frac{AC}{BC}=\frac{-\Delta f}{\Delta x}\).
Получаем: \( \frac{-\Delta f}{\Delta x}=-\ {tg}\alpha \text{ }\Rightarrow \text{ }\frac{\Delta f}{\Delta x}=\ {tg}\alpha \), то есть все, как и в прошлый раз.
Снова устремим точку \( \displaystyle B\) к точке \( \displaystyle A\), и секущая \( \displaystyle AB\) примет предельное положение, то есть превратится в касательную к графику функции в точке \( \displaystyle A\).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
\( {f}’\left( {{x}_{0}} \right)=\ {tg}\varphi =k\)
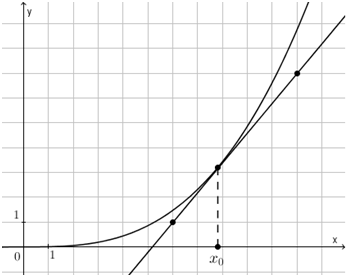
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции \( \displaystyle y=\mathsf{f}\left( x \right)\) и касательная к нему в точке с абсциссой \( {{x}_{0}}\).
Найдите значение производной функции \( \displaystyle \mathsf{f}\left( x \right)\) в точке \( {{x}_{0}}\).
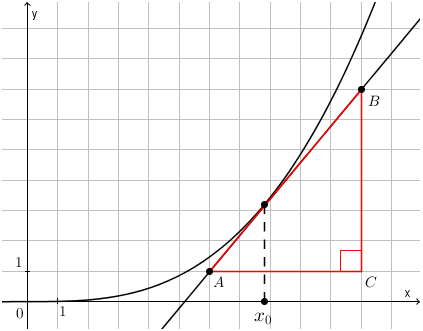
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle f’\left( x \right)=k=\ {tg}\varphi\).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси \( \displaystyle Ox\) – это \( \displaystyle \angle BAC\). Найдем тангенс этого угла:
\( \displaystyle \ {tg}\angle BAC=\frac{BC}{AC}=\frac{6}{5}=1,2\).
Таким образом, производная функции \( \displaystyle \mathsf{f}\left( x \right)\) в точке \( {{x}_{0}}\) равна \( \displaystyle 1,2\).
Ответ: \( \displaystyle 1,2\).
Теперь попробуй сам.
Еще статью на геометрический смысл производной ты найдешь здесь: «Геометрический смысл производной«.
И посмотри так же вебинар на эту тему (ниже в разделе «Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике»)
Решим два примера
Пример 1. На рисунке изображен график функции \( \displaystyle y=\mathsf{f}\left( x \right)\) и касательная к нему в точке с абсциссой \( {{x}_{0}}\). Найдите значение производной функции \( \displaystyle \mathsf{f}\left( x \right)\) в точке \( {{x}_{0}}\);
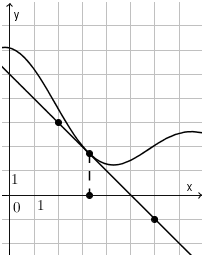
Пример 2. На рисунке изображен график функции \( \displaystyle y=\mathsf{f}\left( x \right)\) и касательная к нему в точке с абсциссой \( {{x}_{0}}\). Найдите значение производной функции \( \displaystyle \mathsf{f}\left( x \right)\) в точке \( {{x}_{0}}\).
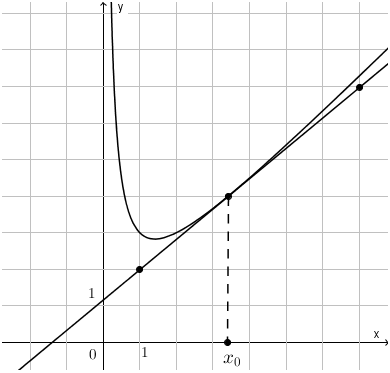
Решение примера №1
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle k=f’\left( x \right)=\ {tg}\beta\).
Достроим треугольник со стороной \( \displaystyle AC\), лежащей на касательной.
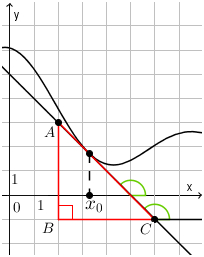
Угол наклона касательной – это угол, отмеченный зеленым на графике.
Он тупой \( \left( >90{}^\circ \right)\), поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла).
Применим знания из тригонометрии:
Решение примера №2
Здесь ответ равен \( \displaystyle \frac{5}{6}\). В ЕГЭ такой ответ написать не получится, но мы ведь должны понимать, что математика не ограничена рамками ЕГЭ.
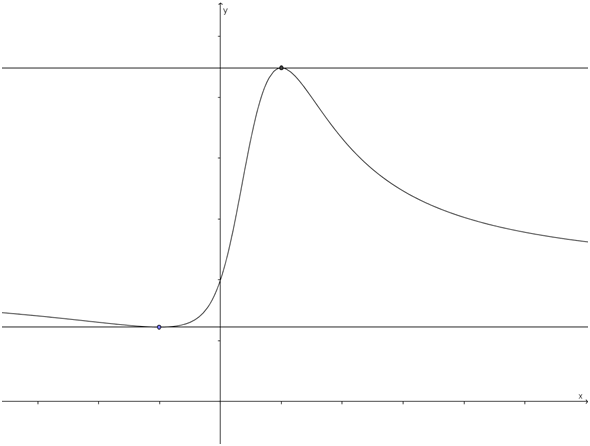
Зная геометрический смысл производной, можно очень просто объяснить правило, что производная в точке локального максимума или минимума равна нулю.
Действительно, касательная к графику в этих точках «горизонтальна», то есть параллельна оси абсцисс:
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, \( f\left( x \right)=\left( {{x}^{2}}+2 \right)\). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке \( {{x}_{0}}\). Например, в точке \( {{x}_{0}}=2\).
Берем линейку, пристраиваем ее к графику и чертим:
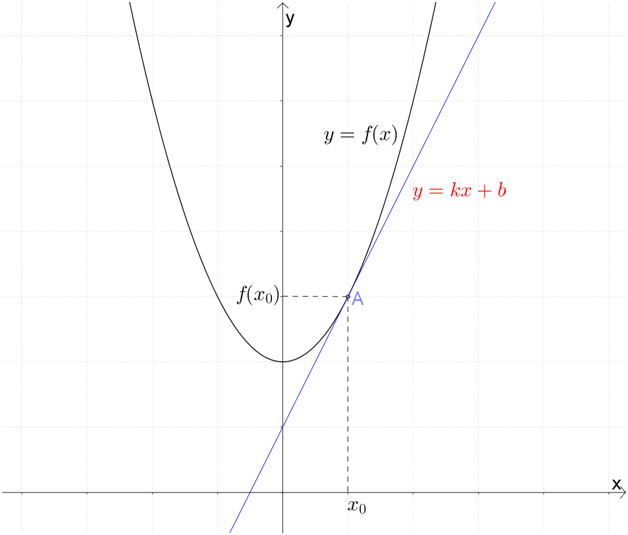
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты \( k\) и \( b\) в уравнении
\( y=kx+b\).
Но ведь \( k\) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
\( k={f}’\left( {{x}_{0}} \right)\).
В нашем примере будет так:
\( {f}’\left( x \right)={{\left( {{x}^{2}}+2 \right)}^{\prime }}=2x;\)\( k={f}’\left( {{x}_{0}} \right)={f}’\left( 2 \right)=2\cdot 2=4.\)
Теперь остается найти \( b\) . Это проще простого: ведь \( b\) – значение \( y\) при \( \displaystyle x=0\).
Графически \( b\) – это координата пересечения прямой с осью ординат (ведь \( \displaystyle x=0\) во всех точках оси \( \displaystyle Oy\)):
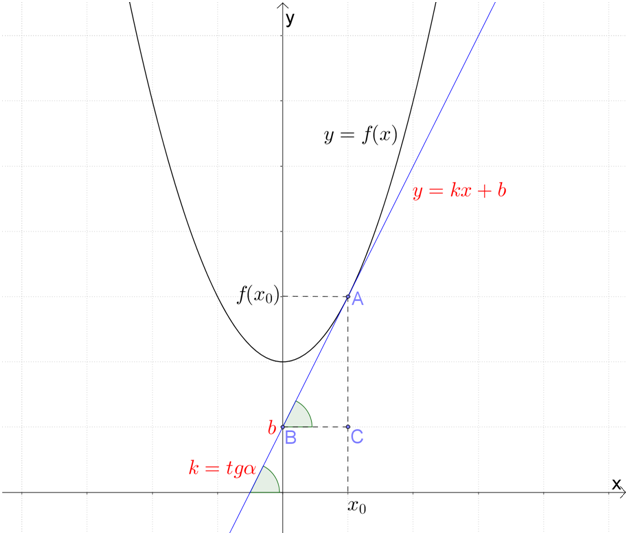
Проведём \( BC\parallel Ox\) (так, что \( \triangle ABC\) – прямоугольный).
Тогда \( \angle ABC=\alpha \)(тому самому углу между касательной и осью абсцисс). Чему равны \( \displaystyle AC\) и \( \displaystyle BC\)?
По рисунку явно видно, что \( BC={{x}_{0}}\), а \( AC=f\left( {{x}_{0}} \right)-b\). Тогда получаем:
\( {f}’\left( {{x}_{0}} \right)=\ {tg}\alpha =\frac{AC}{BC}=\frac{f\left( {{x}_{0}} \right)-b}{{{x}_{0}}}\text{ }\Rightarrow \text{ }b=f\left( {{x}_{0}} \right)-{{x}_{0}}\cdot {f}’\left( {{x}_{0}} \right)\).
Соединяем все полученные формулы в уравнение прямой:
\( y=kx+b={f}’\left( {{x}_{0}} \right)\cdot x+f\left( {{x}_{0}} \right)-{{x}_{0}}\cdot {f}’\left( {{x}_{0}} \right);\)\( y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\)
Это и есть уравнение касательной к графику функции \( f\left( x \right)\) в точке \( {{x}_{0}}\).
Пример:
Найди уравнение касательной к графику функции \( f\left( x \right)={{x}^{2}}-2x+3\) в точке \( {{x}_{0}}=3\).
Решение:
На этом примере выработаем простой…
Алгоритм действий для нахождения уравнения касательной
| Алгоритм | Пример: \( f\left( x \right)={{x}^{2}}-2x+3\), \( {{x}_{0}}=3\) |
| 1. Вычислим \( f\left( {{x}_{0}} \right)\) | \( f\left( {{x}_{0}} \right)=f\left( 3 \right)={{3}^{2}}-2\cdot 3+3=6\) |
| 2. Найдём формулу производной функции \( {f}’\left( x \right)\) | \( {f}’\left( x \right)={{\left( {{x}^{2}}-2x+3 \right)}^{\prime }}=2x-2\) |
| 3. Вычислим \( {f}’\left( {{x}_{0}} \right)\) | \( {f}’\left( {{x}_{0}} \right)={f}’\left( 3 \right)=2\cdot 3-2=4\) |
| 4. Подставим \( {{x}_{0}},\text{ }f\left( {{x}_{0}} \right)\) и \( {f}’\left( {{x}_{0}} \right)\) в формулу уравнения касательной \( y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)\) | \( \begin{array}{l}y={f}’\left( {{x}_{0}} \right)\cdot \left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)=\\\text{ }=4\left( x-3 \right)+6=4{x} -12+6=\\\text{ }=4{x} -6\end{array}\) |
Пять примеров для самостоятельной работы
Разбор примеров:
Пример 1. Все по алгоритму
\( y\left( {{x}_{0}} \right)=y\left( -2 \right)=\frac{2\cdot \left( -2 \right)}{{{\left( -2 \right)}^{2}}-1}=-\frac{4}{3}\).
Пример 2
То, что нам известен угол наклона касательной, очень хорошо: ведь его тангенс равен производной функции, а также угловому коэффициенту \( \displaystyle k\) касательной.
Но тут есть подвох: дело в том, что под углом \( \displaystyle 45{}^\circ \) ось \( \displaystyle Ox\) могут пересекать две разные касательные: с наклоном «вправо» и «влево»:
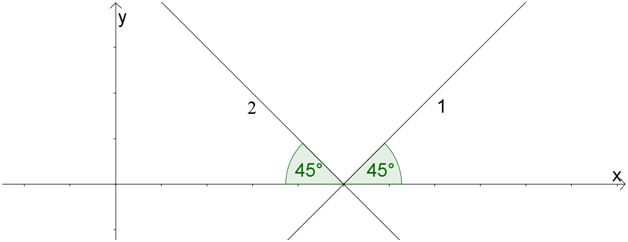
Прямая 2 (та, которая «наклонена влево») с положительным направлением оси \( \displaystyle Ox\) составляет угол \( 180{}^\circ -45{}^\circ =135{}^\circ \) – это и есть угол наклона прямой к оси \( \displaystyle Ox\).
Пример 3
Абсцисса – это ось \( \displaystyle Ox\), а значит, нам нужно найти значение \( \displaystyle x\) в точке пересечения касательной и графика функции.
Из уравнения \( \displaystyle k=f’\left( x \right)=\ {tg}\beta \) мы знаем, что угловой коэффициент наклона касательной равен значению производной в точке касания.
Поскольку прямая \( \displaystyle y=13x+5\) параллельна касательной, это значит, что их угловые коэффициенты наклона одинаковые \( \displaystyle \left( k=13 \right)\).
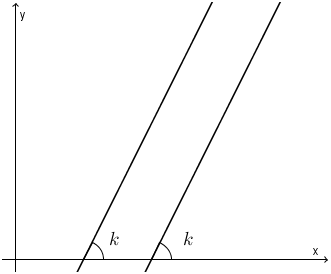
Согласно правилам вычисления производных, находим производную функции \( \displaystyle y=4{{x}^{2}}+5{x}-13\):
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Сдай ЕГЭ на 90+ с автором этого учебника
Алексей Шевчук — учитель с 20-летним стажем
математика, информатика, физика
Запишитесь на занятия:
+7 (905) 541-39-06
alexei.shevchuk@youclever.org


